笔记-神经网络滑模控制设计方法

神经网络滑模控制

前面介绍的万能逼近原理中，主要的万能逼近器有：多项式函数逼近器、神经网络逼近器、T-S模糊系统。学习文献[1]后，对神经网络滑模控制进行介绍和总结。

文献[1]第九章介绍：

如果被控对象的数学模型已知，滑模控制器可以使系统输出直接跟踪期望指令，但较大的建模不确定性需要较大的切换增益，这就造成了抖振，抖振是滑模控制中难以避免的问题。
将滑模控制结合神经网络逼近用于非线性系统的控制中，采用神经网络实现模型未知部分的自适应逼近，可以有效降低模糊增益 (?) 。神经网络自适应律通过Lyapunov方法导出，通过自适应权重调节，保证整个闭环系统的稳定性和收敛性。
RBF(Radial Basis Function, 径向基函数)神经网络具有良好的泛化能力，网络结构简单，避免不必要的和冗长的计算，能在一个紧凑集和任意精度下，逼近任何非线性函数。

神经网络控制策略的优点：

1. 神经网络对任意函数具有学习能力，神经网络的自学习能力可避免在传统自适应控制理论中占据重要地位的复杂数学分析。
2. 针对传统控制方法不能解决的高度非线性控制问题，多层神经网络的隐含层神经元采用了具有非线性映射功能的激活函数，这种映射可以逼近任意非线性函数，为解决非线性控制问题提供了有效的解决途径。
3. 传统自适应控制方法需要模型先验信息来设计控制方案，如需要建立被控对象的数学模型。由于神经网络的自学习能力，控制器不需要许多系统的模型和参数信息。因此，神经网络控制可以广泛应用于解决具有不确定模型的控制问题。
4. 采用神经元芯片或并行硬件，为大规模神经网络并行处理提供了非常快速的多处理技术。
5. 在神经网络的大规模并行处理架构下，网络的某些节点损坏并不影响整个神经网络的整体性能，有效地提高了控制系统的容错性。

针对MIMO模型，常规控制器的设计方法一般要求建立最小相位系统的结构和精确的数学模型，在许多情况下模型参数还要求精确已知。神经网络可以通过前向或反向的动态行为在线学习复杂模型，通过适应环境的变化设计自适应MIMO控制器。从理论上讲，一个基于神经网络的控制系统的设计相对简单，因为它不要求有关该模型的任何先验知识。以上，都需要真实数据进行投喂，数据可靠性越高，量越大，拟合模型越精确，控制器效果越好。

一、RBF神经网络介绍^[2]

1. 什么是径向基函数

1985年，Powell提出了多变量插值的径向基函数方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是$\Phi (x)=\Phi (||x||)$，或者还可以是到任意一点c的距离，c点称为中心点，也就是$\Phi (x,c)=\Phi (||x-c||)$。任意一个满足$\Phi (x)=\Phi (||x||)$特性的函数$\Phi$都叫做径向基函数，标准的一般使用欧氏距离(也叫做欧式径向基函数)，尽管其他距离函数也是可以的。最常用的径向基函数是高斯核函数 ,形式为
$$k\left(||x-x_c||\right)=e^{-\frac{||x-x_c|{|}^2}{(2\sigma {)}^2}}$$

其中，$x_c$为核函数中心，$\sigma$为函数的宽度参数 , 控制了函数的径向作用范围。

图1：RBF神经网络示意图

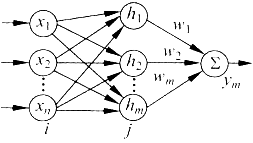
RBF神经网络有3层，输入层、隐含层和输出层。隐含层的神经元激活函数由径向基函数构成。隐含层组成的数组运算单元称为隐含层节点。每个隐含层节点包含一个中心向量$\mathbf{c}$，该向量和输入参数向量$\mathbf{x}$具有相同的维数，二者之间的欧氏距离定义为$||x(t)-c_j(t)||$。隐含层的输出由非线性激活函数$h_j(t)$构成：
$$h_j(t)=\exp \left(-\frac{||\mathbf{x}-{\mathbf{c}}_j(t)|{|}^2}{2b_j^2}\right),j=1,\cdots ,m$$

其中，$b_j$是一个正的标量，表示高斯基函数的宽度，$m$是隐含层的节点数量。网络的输出由如下加权函数实现：
$$y_i(t)=\sum _{j=1}^m{w}_{ji}{h}_j(t),i=1,\cdots ,n$$

其中，$w$是输出层的权值，$n$是输出节点的个数，$y$是神经网络输出。

2. RBF神经网络

RBF神经网络效果

神经网络最小参数学习法

通过参数的估计代替神经网络权值的调整，自适应算法简单，便于实际工程应用。

二、一种简单的RBF网络自适应滑模控制

1. 控制器设计

考虑一种简单的动力学系统：
$$\ddot{\theta }=f(\theta ,\dot{\theta })+u\text{\hspace{1em}(1)}$$

其中，$\theta$是转动角度，$u$为控制输入。

写成状态方程的形式：
$$\{\begin{array}{rl}{\dot{x}}_1& =x_2\\ {\dot{x}}_2& =f(x)+u\end{array}\text{\hspace{1em}(2)}$$

其中，$f(x)$为未知项。

位置指令为$x_d$，则误差及其导数为：
$$e=x_1-x_d,\dot{e}=x_2-{\dot{x}}_d\text{\hspace{1em}(3)}$$

定义滑模函数：
$$s=ce+\dot{e}\text{\hspace{1em}(4)}$$

则：
$$\dot{s}=c\dot{e}+\ddot{e}=c\dot{e}+{\dot{x}}_2-{\ddot{x}}_d=c\dot{e}+f(x)+u-{\ddot{x}}_d$$

由于RBF神经网络具有万能逼近特性，采用RBF神经网络逼近$f(x)$，算法为：
$$\begin{array}{rl}{h}_j& =\exp \left(\frac{||\mathbf{x}-{\mathbf{c}}_j|{|}^2}{2b_j^2}\right)\\ f& ={\mathbf{W}}^{\ast T}\mathbf{h}(\mathbf{x})+\epsilon \end{array}\text{\hspace{1em}(5)}$$

其中，$\mathbf{x}$为网络的输入，$j$为网络隐含层第$j$个节点，$\mathbf{h}(\mathbf{x})=[h_j{]}^{\text{T}}$为网络的高斯基函数输出，${\mathbf{W}}^{\ast }$为网络的理想权值 （为常数），$\epsilon$为网络的逼近误差，$|\epsilon |\le {\epsilon }_N$。

由于
$$f(x)-\hat{f}(x)={\mathbf{W}}^{\ast \text{T}}\mathbf{h}(\mathbf{x})+\epsilon -{\hat{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{x})={\tilde{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{x})+\epsilon \text{\hspace{1em}(6)}$$

定义Lyapunov函数为：
$$V=\frac{1}{2}{s}^2+\frac{1}{2\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\tilde{\mathbf{W}}$$

其中，$\gamma >0$，$\tilde{\mathbf{W}}=\hat{\mathbf{W}}-{\mathbf{W}}^{\ast }$。

对上式求导，可得：
$$\begin{array}{rl}\dot{V}& =s\dot{s}+\frac{1}{\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\dot{\tilde{\mathbf{W}}}=s\dot{s}+\frac{1}{\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\dot{\hat{\mathbf{W}}}\\ & =s(c\dot{e}+f(x)+u-{\ddot{x}}_d)+\frac{1}{\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\dot{\hat{\mathbf{W}}}\end{array}\text{\hspace{1em}(7)}$$

设计控制律为：
$$u=-c\dot{e}-\hat{f}(x)+{\ddot{x}}_d-\eta \text{sgn}(s)\text{\hspace{1em}(8)}$$

将式$(8)$代入式$(7)$，可得：
$$\begin{array}{rl}\dot{V}& =s(f(x)-\hat{f}(x)-\eta \text{sgn}(s))+\frac{1}{\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\dot{\hat{\mathbf{W}}}\\ & =s(-{\tilde{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{x})+\epsilon -\eta \text{sgn}(s))+\frac{1}{\gamma }{\tilde{\mathbf{W}}}^{\text{T}}\dot{\hat{\mathbf{W}}}\\ & =\epsilon s-\eta |s|+{\tilde{\mathbf{W}}}^{\text{T}}\left(\frac{1}{\gamma }\dot{\hat{\mathbf{W}}}-s\mathbf{h}(\mathbf{x})\right)\end{array}\text{\hspace{1em}(9)}$$

取$\eta >{\epsilon }_N$，自适应律为：
$$\dot{\hat{\mathbf{W}}}=\gamma s\mathbf{h}(\mathbf{x})\text{\hspace{1em}(10)}$$

令$\eta ={\eta }_0+{\epsilon }_N,{\eta }_0>0$，则式$(9)$可化为：
$$\dot{V}=\epsilon s-\eta |s|\le -{\eta }_0|s|\le 0$$

当$\dot{V}\equiv 0$时，$s\equiv 0$，根据LaSalle不变集原理，闭环系统渐近稳定，即$t\to \infty$时，$s\to 0$。由于$V\ge 0$且$\dot{V}\le 0$，则当$t\to \infty$时，$V$有界，则$\hat{\mathbf{W}}$有界，但无法保证收敛于$\mathbf{W}$。控制律$(8)$中的鲁棒项$\eta \text{sgn}(s)$的作用是克服神经网络的逼近误差，以保证系统稳定性。

问题：

1. 高斯基函数中的参数${\mathbf{c}}_i$和$b_i$如何取值？
2. RBF神经网络的权值如何取？按自适应律$(10)$来取值。
3. 逼近误差$\epsilon$的上界${\epsilon }_N$是多少？
4. 控制律中的参数$\gamma$和$\eta$如何取值？对系统的控制效果会产生什么影响？

2. 仿真分析

图2：f(x)及其估计\hat{f}(x)

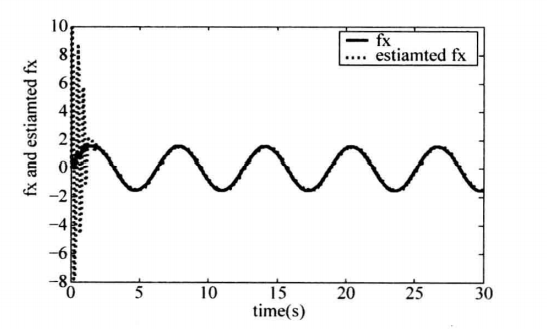
详细过程见参考文献[1]第九章。其他方法与之类似，都是用神经网络逼近模型未知部分，下面一种方法是用神经网络直接拟合控制律，因为控制律也是一个未知函数。

三、基于神经网络的直接自适应滑模控制

1. 控制律设计

考虑如下非线性二阶系统：
$$\{\begin{array}{rl}{\dot{x}}_1& =x_2\\ {\dot{x}}_2& =\alpha (\mathbf{x})+\beta (\mathbf{x})u\\ y& =x_1\end{array}\text{\hspace{1em}(11)}$$

其中，。。。。。$\alpha (\mathbf{x})$和$\beta (\mathbf{x})$未知光滑函数，$\beta (\mathbf{x})>0$，$|\beta (\mathbf{x})|\le \bar{\beta }$。定义$\mathbf{x}=[x_1,x_2{]}^{\text{T}}\in \mathbb{R}$。

定义向量${\mathbf{x}}_d$、$\mathbf{e}$和滑模函数$s$：
$$\begin{array}{rl}{\mathbf{x}}_d& =[y_d,{\dot{y}}_d{]}^{\text{T}}\\ \mathbf{e}& =\mathbf{x}-{\mathbf{x}}_d=[e,\dot{e}{]}^{\text{T}}\\ s& =[\lambda ,1]\mathbf{e}=\lambda e+\dot{e}\end{array}$$

其中，$\lambda >0$。对滑模函数$s$求导，可得：
$$\dot{s}=\lambda \dot{e}+\ddot{e}=\cdots =\alpha (\mathbf{x})+v+\beta (\mathbf{x})u\text{\hspace{1em}(12)}$$

其中，$v=-{\ddot{y}}_d+\lambda \dot{e}$。

那么，针对被控对象$(11)$，理想滑模控制器为 （这里不应该采用这种比较复杂的滑模控制器，or应该说明为什么采用这种控制器）：
$$u^{\ast }=-\frac{1}{\beta (\mathbf{x})}(\alpha (\mathbf{x})+v)-\left(\frac{1}{\epsilon \beta (\mathbf{x})}+\frac{1}{\epsilon {\beta }^2(\mathbf{x})}-\frac{\dot{\beta }(\mathbf{x})}{2{\beta }^2(\mathbf{x})}\right)s\text{\hspace{1em}(13)}$$

其中，$\epsilon >0$。

由$u^{\ast }$的表达式可知，$u^{\ast }$为关于$\mathbf{x}$、$s$、$\epsilon$、$v$的连续函数，所以可以采用RBF神经网络来逼近$u^{\ast }$，则该函数的神经网络输入可表示为 （为什么这么选呢？为了提高网络逼近的精度）：
$$\mathbf{z}={\left[\mathbf{x},s,\frac{s}{\epsilon },v\right]}^{\text{T}}\in {\Omega }_z\subset {\mathbb{R}}^5\text{\hspace{1em}(14)}$$

存在理想的网络权值${\mathbf{W}}^{\ast }$，使得：
$$u^{\ast }(\mathbf{z})={\mathbf{W}}^{\ast \text{T}}\mathbf{h}(\mathbf{z})+{\mu }_l\text{\hspace{1em}(15)}$$

其中，$\mathbf{h}(\mathbf{z})$为高斯基函数，${\mu }_l$为网络的逼近误差，且满足$|{\mu }_l|\le {\mu }_0$。因此可得：
$${\mathbf{W}}^{\ast }=\arg \underset{\mathbf{W}\in {\mathbb{R}}^l}{\min }\left\{\underset{\mathbf{z}\in {\Omega }_z}{\sup }|{\mathbf{W}}^{\text{T}}\mathbf{h}(\mathbf{z})-u^{\ast }(\mathbf{z})\right\}\text{\hspace{1em}(16)}$$

控制律设计为RBF神经网络的输出，即：
$$u={\hat{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{z})\text{\hspace{1em}(17)}$$

其中，$\hat{\mathbf{W}}$是${\mathbf{W}}^{\ast }$的估计值。

自适应律设计为 (why)：
$$\dot{\hat{\mathbf{W}}}=-\mathbf{\Gamma }(\mathbf{h}(\mathbf{z})s+\sigma \hat{\mathbf{W}})\text{\hspace{1em}(18)}$$

其中，$\mathbf{\Gamma }={\mathbf{\Gamma }}^{\text{T}}>0$，$\sigma >0$。

将控制器$(17)$代入式$(12)$，得：
$$\dot{s}=\alpha (\mathbf{x})+v+\beta (\mathbf{x}){\hat{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{z})\text{\hspace{1em}(19)}$$

将式$(15)$代入式$(19)$，可得 （这里相对于把约束条件“0=0”代入）：
$$\dot{s}=\alpha (\mathbf{x})+v+\beta (\mathbf{x})\left({\hat{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{z})-{\mathbf{W}}^{\ast \text{T}}\mathbf{h}(\mathbf{z})-{\mu }_l\right)+\beta (\mathbf{x})u^{\ast }(\mathbf{z})\text{\hspace{1em}(20)}$$

进一步将理想滑模控制器$(13)$代入上式，经化简后可得：
$$\dot{s}=\beta (\mathbf{x})\left({\tilde{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{z})-{\mu }_l\right)-\left(\frac{1}{\epsilon }+\frac{1}{\epsilon \beta (\mathbf{x})}-\frac{\dot{\beta }(\mathbf{x})}{2\beta (\mathbf{x})}\right)s\text{\hspace{1em}(21)}$$

其中，$\tilde{\mathbf{W}}=\hat{\mathbf{W}}-{\mathbf{W}}^{\ast }$。

为了防止$\beta (\mathbf{x})$项包含在自适应律$\dot{\hat{\mathbf{W}}}$中，在Lyapunov函数中取$\frac{1}{2}\frac{s^2}{\beta (\mathbf{x})}$替代$\frac{1}{2}{s}^2$ (这里用到了$\beta (\mathbf{x})>0$)的条件，则Lyapunov函数设计为：
$$V=\frac{1}{2}\left(\frac{s^2}{\beta (\mathbf{x})}+{\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\tilde{\mathbf{W}}\right)\text{\hspace{1em}(22)}$$

对上式求导 （这里也用了控制律是个慢变量的条件，是不是理解错了？？是的！！） 并将式$(18)$和$(21)$代入，可得，可得：
$$\begin{array}{rl}\dot{V}& =\frac{s\dot{s}}{\beta (\mathbf{x})}-\frac{\dot{\beta }(\mathbf{x})s^2}{{\beta }^2(\mathbf{x})}+{\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\dot{\hat{\mathbf{W}}}\\ & =\frac{s}{\beta (\mathbf{x})}\left(\beta (\mathbf{x})\left({\tilde{\mathbf{W}}}^{\text{T}}\mathbf{h}(\mathbf{z})-{\mu }_l\right)-\left(\frac{1}{\epsilon }+\frac{1}{\epsilon \beta (\mathbf{x})}-\frac{\dot{\beta }(\mathbf{x})}{2\beta (\mathbf{x})}\right)s\right)\\ & -\frac{\dot{\beta }(\mathbf{x})s^2}{{\beta }^2(\mathbf{x})}+{\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\left(-\mathbf{\Gamma }(\mathbf{h}(\mathbf{z})s+\sigma \hat{\mathbf{W}})\right)\\ & =-\left(\frac{1}{\epsilon \beta (\mathbf{x})}+\frac{1}{\epsilon {\beta }^2(\mathbf{x})}\right)s^2-{\mu }_{l}s-\sigma {\tilde{\mathbf{W}}}^{\text{T}}\hat{\mathbf{W}}\end{array}\text{\hspace{1em}(23)}$$

由于：
$$\begin{array}{rl}2{\tilde{\mathbf{W}}}^{\text{T}}\hat{\mathbf{W}}& ={\tilde{\mathbf{W}}}^{\text{T}}\left(\tilde{\mathbf{W}}+{\mathbf{W}}^{\ast }\right)+{\left(\hat{\mathbf{W}}-{\mathbf{W}}^{\ast }\right)}^{\text{T}}\hat{\mathbf{W}}\\ & ={\tilde{\mathbf{W}}}^{\text{T}}\tilde{\mathbf{W}}+{\left(\hat{\mathbf{W}}-{\mathbf{W}}^{\ast }\right)}^{\text{T}}{\hat{\mathbf{W}}}^{\ast }+{\hat{\mathbf{W}}}^{\text{T}}\hat{\mathbf{W}}-{\mathbf{W}}^{\ast \text{T}}\hat{\mathbf{W}}\\ & =||\tilde{\mathbf{W}}|{|}^2+||\hat{\mathbf{W}}|{|}^2-||{\mathbf{W}}^{\ast }|{|}^2\\ & \ge ||\tilde{\mathbf{W}}|{|}^2-||{\mathbf{W}}^{\ast }|{|}^2\end{array}\text{\hspace{1em}(24)}$$

和 （$2ab\le a^2+b^2$）
$$|{\mu }_{l}s|\le \frac{s^2}{2\epsilon \beta (\mathbf{x})}+\frac{\epsilon }{2}{\mu }_l^2\beta (\mathbf{x})\le \frac{s^2}{2\epsilon \beta (\mathbf{x})}+\frac{\epsilon }{2}{\mu }_l^2\bar{\beta }\text{\hspace{1em}(25)}$$

又由于$|{\mu }_l|\le {\mu }_0$，将式$(24)$和$(25)$代入式$(23)$，式$(23)$可以进一步化为：
$$\dot{V}\le -\frac{s^2}{2\epsilon \beta (\mathbf{x})}-\frac{\sigma }{2}||\tilde{\mathbf{W}}|{|}^2+\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\text{\hspace{1em}(26)}$$

又由于${\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\tilde{\mathbf{W}}\le \bar{\gamma }||\tilde{\mathbf{W}}|{|}^2$，（$\bar{\gamma }$为${\mathbf{\Gamma }}^{-1}$的最大特征值），故上式可以进一步化为：
$$\begin{array}{rl}\dot{V}& \le -\frac{1}{2}\left(\frac{s^2}{\epsilon \beta (\mathbf{x})}+\frac{\sigma }{\bar{\gamma }}{\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\tilde{\mathbf{W}}\right)+\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\\ & \le -\frac{1}{{\alpha }_0}\frac{1}{2}\left(\frac{s^2}{\beta (\mathbf{x})}+{\tilde{\mathbf{W}}}^{\text{T}}{\mathbf{\Gamma }}^{-1}\tilde{\mathbf{W}}\right)+\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\\ & =-\frac{1}{{\alpha }_0}V+\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\end{array}\text{\hspace{1em}(27)}$$

其中， α 0 = max ⁡ { ε , γ ˉ / σ } \alpha_0 = \max\{ \varepsilon, \bar \gamma /\sigma \} α0​=max{ε,γˉ​/σ}。

这里，需要通过选择适当的参数${\alpha }_0$、$\bar{\beta }$、$\sigma$和${\mu }_0$，来确保$\frac{1}{{\alpha }_0}V>\frac{\epsilon }{2}{\mu }_l^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2$，${\mathbf{W}}^{\ast }$未知，也无法保证哇！！

根据引理1，求解不等式$(27)$，取$t(0)=0$，可得：
$$\begin{array}{rl}V(t)& \le e^{-\frac{t}{{\alpha }_0}}V(0)+\left(\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\right){\int }_0^t{e}^{-\frac{t-\tau }{{\alpha }_0}}\text{d}\tau \\ & \le e^{-\frac{t}{{\alpha }_0}}V(0)+{\alpha }_0\left(\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\right),\forall t\ge 0\end{array}\text{\hspace{1em}(28)}$$

由于$V(0)$有界，则式$(28)$表明，$V(t)$是有界的，因此$s$和$\hat{\mathbf{W}}(t)$有界。也就只能证明到这一步了。
$$\underset{t\to \infty }{\lim }V(t)\le {\alpha }_0\left(\frac{\epsilon }{2}{\mu }_0^2\bar{\beta }+\frac{\sigma }{2}||{\mathbf{W}}^{\ast }|{|}^2\right)\text{能说明什么问题呢？}$$

问题：

1. 由于${\mathbf{W}}^{\ast }$未知，无法由式$(27)$来证明控制器$(17)$的收敛性哇！！收敛速度也无法保证！
2. 在式$(28)$中，如何证明${\int }_0^t{e}^{-\frac{t-\tau }{{\alpha }_0}}\text{d}\tau \le {\alpha }_0$? （简单，已解决）
3. 参数太多，如何选择参数？
4. 这么复杂，可能还不如简单的PID效果好，路跑偏了吧！

---

引理1： 针对$V:[0,\infty )\in \mathbb{R}$，不等式方程$\dot{V}\le -\alpha V+f,\forall t\ge t_0\ge 0$的解为：
$$V(t)\le e^{-\alpha (t-t_0)}V(t_0)+{\int }_{t_0}^t{e}^{-\alpha (t-\tau )}f(\tau )\text{d}\tau$$

其中，$\alpha$为任意常数。

当$f=0$，则$\dot{V}\le -\alpha V$的解为：
$$V(t)\le e^{-\alpha (t-t_0)}V(t_0)$$

如果$\alpha$为正实数，则$V(t)$以指数形式收敛于0。

2. 仿真分析

详细过程见参考文献[1]第九章9.4节。

---

参考文献

1. 刘金琨. 滑模变结构控制MATLAB仿真：基本理论与设计方法[M]. 清华大学出版社, 2015.
2. RBF（径向基函数）神经网络
3. 刘金琨. RBF神经网络自适应控制matlab仿真[M]. 清华大学出版社, 2014.