《ELSED: Enhanced Line SEgment Drawing》源码阅读笔记之直线拟合+数学公式

paper:https://arxiv.org/pdf/2108.03144.pdf

github source code:GitHub - iago-suarez/ELSED: ELSED: Enhanced Line SEgment Drawing

一、最小二乘直线拟合

公式：使用Online Equation Editor - standalone查看calculateLineEq方法注释上的公式

补充上图公式的理解:

直线拟合——最小二乘法、hough变换 - 知乎https://zhuanlan.zhihu.com/p/363278784

一个是 a+bx, 一个是b+ax， 点斜式和一般式的变换

 

 

 

inline void FullSegmentInfo::leastSquareLineFit(const std::vector<Pixel> &pts, int startIdx) {
  int i, indpCoord, depCoord;
  sum_x_i = 0, sum_y_i = 0, sum_x_i_y_i = 0, sum_x_i_2 = 0;
  N = pts.size() - startIdx;
  if (isHorizontal) {
    for (i = startIdx; i < pts.size(); i++) {
      indpCoord = pts[i].x;
      depCoord = pts[i].y;
      sum_x_i += indpCoord;
      sum_y_i += depCoord;
      sum_x_i_2 += indpCoord * indpCoord;
      sum_x_i_y_i += indpCoord * depCoord;
    }
  } else {
    for (i = startIdx; i < pts.size(); i++) {
      indpCoord = pts[i].y;
      depCoord = pts[i].x;
      sum_x_i += indpCoord;
      sum_y_i += depCoord;
      sum_x_i_2 += indpCoord * indpCoord;
      sum_x_i_y_i += indpCoord * depCoord;
    }
  }

  calculateLineEq();
}

inline void FullSegmentInfo::calculateLineEq() {
  // Line equation is calculated as:
  //     \[
  //    ax + by + c = 0 \left\{
  //    \begin{array}{ll}
  //    a = N \cdot \sum (x_i y_i) - \sum x_i \cdot \sum y_i\\
  //    b = \left( \sum x_i \right )^2 - N \cdot \sum x_i^2\\
  //    c = \sum y_i \cdot \sum x_i^2 - \sum x_i \cdot \sum x_i y_i
  //    \end{array}
  //    \right.
  //    \]
  // Compute the line equation coefficients
  equation[2] = sum_y_i * sum_x_i_2 - sum_x_i * sum_x_i_y_i;
  if (isHorizontal) {
    equation[0] = N * sum_x_i_y_i - sum_x_i * sum_y_i;
    equation[1] = sum_x_i * sum_x_i - N * sum_x_i_2;
  } else {
    equation[1] = N * sum_x_i_y_i - sum_x_i * sum_y_i;
    equation[0] = sum_x_i * sum_x_i - N * sum_x_i_2;
  }

  // Normalize the line equation
  equation *= (1 / std::sqrt(equation[0] * equation[0] + equation[1] * equation[1]));

//为什么要这么做???

  // Fix the line equation
  if (dx * -equation[1] + dy * equation[0] < 0) {
    equation[0] = -equation[0];
    equation[1] = -equation[1];
    equation[2] = -equation[2];
  }
}

二、计算直线拟合的均方误差，点到直线的距离

公式：记住平面坐标系中点到直线距离公式的证明思想

  inline double getFitError() const {
    double dist, fitError = 0;
    for (int i = firstPxIndex; i <= lastPxIndex; i++) {
      dist = equation[0] * (*pixels)[i].x + equation[1] * (*pixels)[i].y + equation[2];
      fitError += dist * dist;
    }
    return fitError / N;
  }

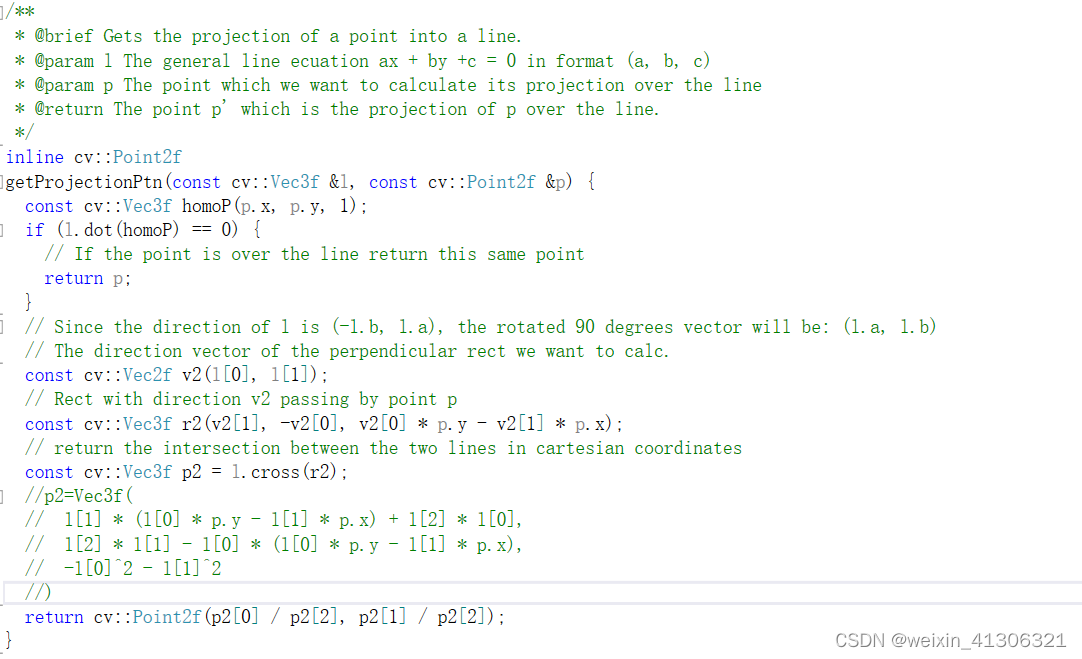
三、获取点到直线的投影

公式:点在直线上的投影点_RobotLife的博客-CSDN博客_点在直线上的投影