[补充]特征值 特征向量

---

• 配图

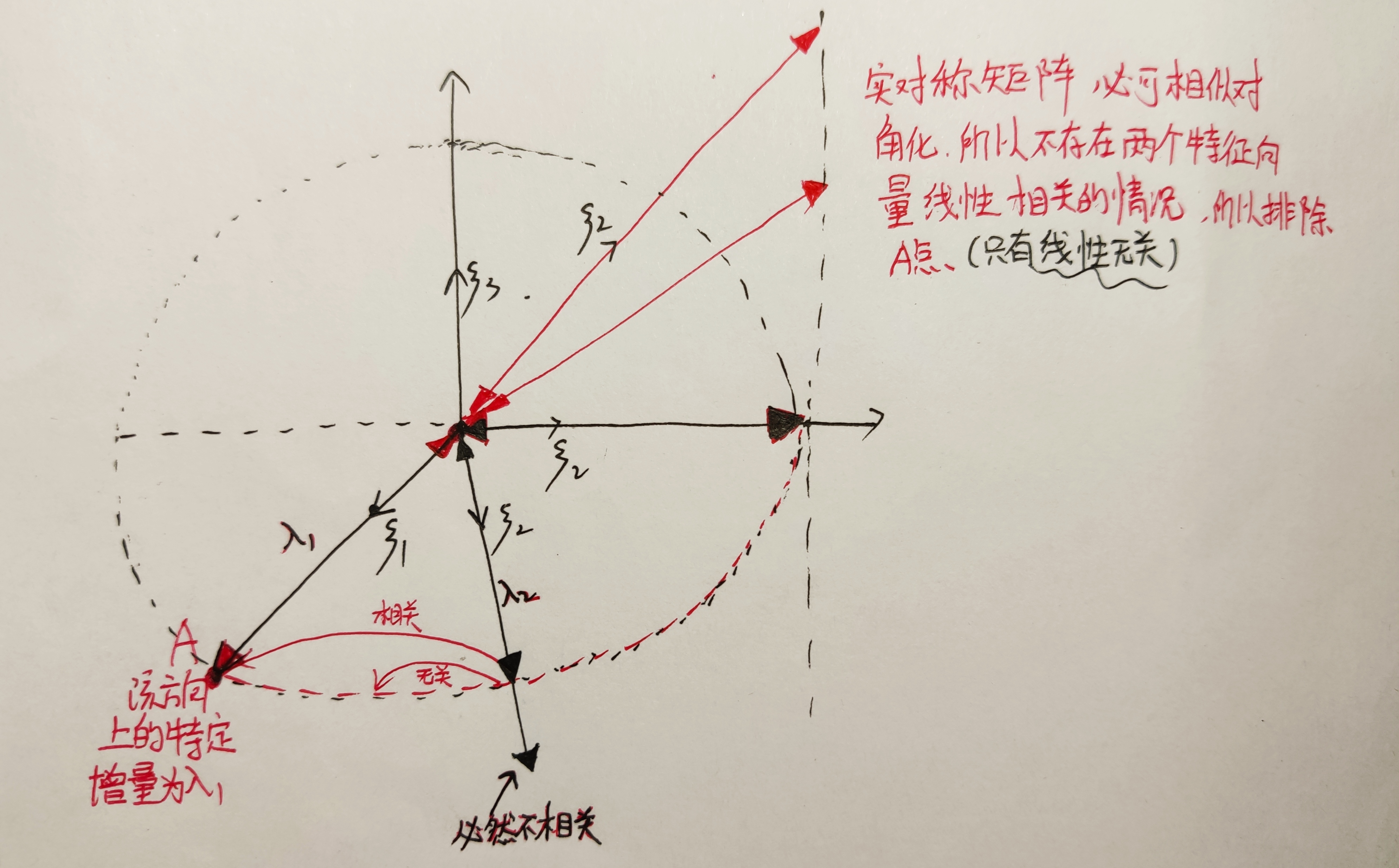
1. 不同的特征值的特征向量一定线性无关，普通矩阵特征值相同的特征向量可能线性相关，也可能线性无关，实对称矩阵特征值相同的特征向量线性无关。

2. k重特征值至多只有k个线性无关的特征向量(也可能没有的)

3. 定理三描述的是：以特征值为λ的特征向量(基本属性-能量相同)作为基础解析，来表示符合特征值为λ的所有特征向量(方向不同)

4. 矩阵A(n阶)满足有n个线性无关的特征向量(⚐每个ki重特征值都有ki个线性无关的特征向量)，即可相似对角化。特征值可以不全相同，因为相同的特征值的特征向量可以线性无关，但是有n个不同的特征值时，满足了不同特征值的特征向量线性无关，所以是充分条件，而非必要条件。
   ⚐:换言之就是特征值相同的特征向量是线性无关的

5. 实对称矩阵必相似于对角矩阵，因为必可相似对角化，但可相似对角化不能推出矩阵是实对称矩阵，因为n个线性无关的特征向量不能保证红色部分的特征向量存在，即不能保证不同特征值的特征向量线性无关。

---

• 辅助理解

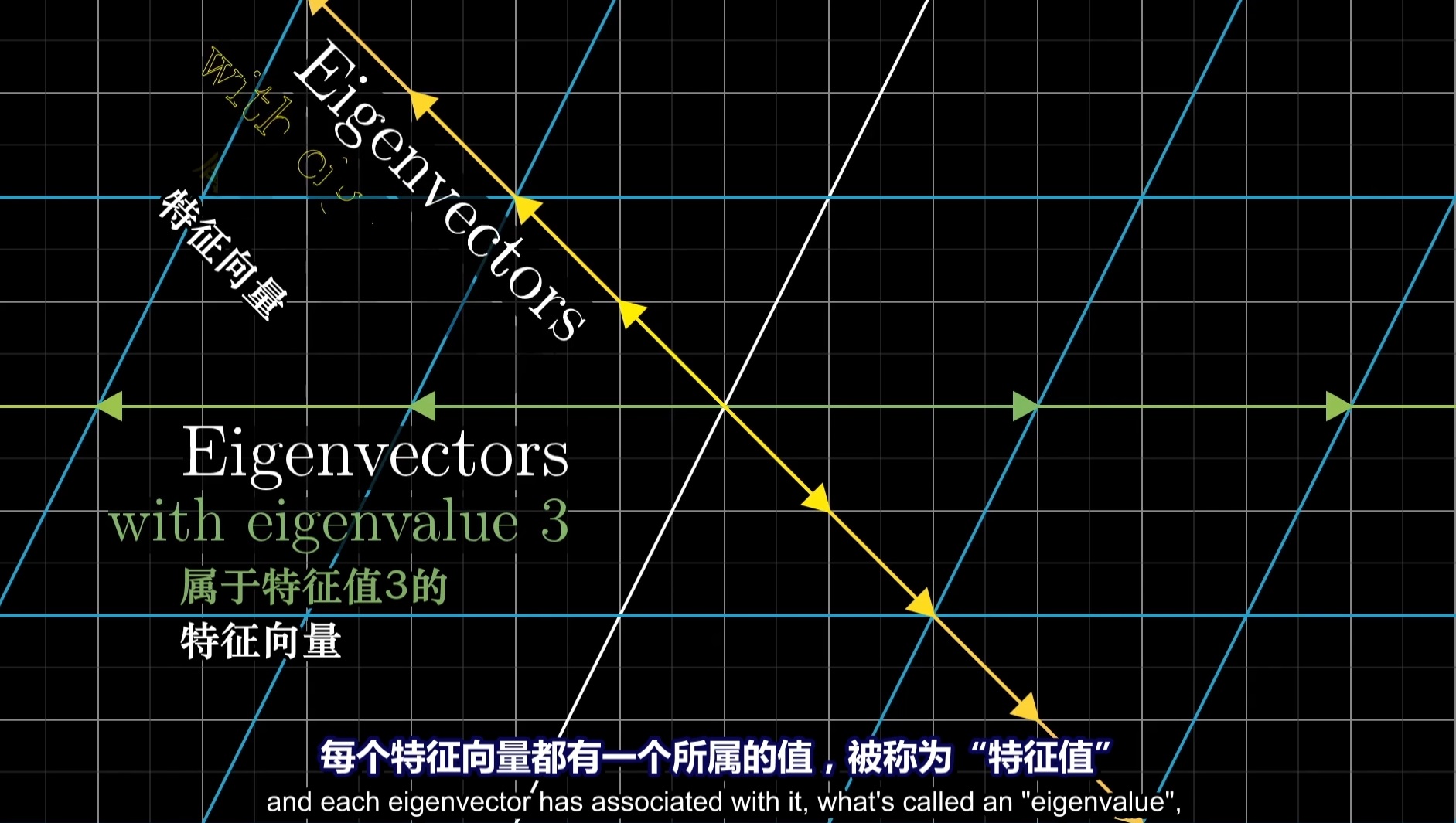
根据特征向量数学公式定义，A ξ = λ ξ，矩阵乘以一个向量的结果仍是同维数的一个向量，矩阵乘法对应了一个变换，把一个向量变成同维数的另一个向量，除了零向量，有没有其他向量可以在向量空间变换完不改变方向的？(注意：特征向量不能是零向量)

所以一个变换的特征向量是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已。

特征值只不过反映了特征向量在变换时的伸缩倍数而已，对一个变换而言，特征向量指明的方向是很重要的，特征值似乎不是那么重要；但是，引用了谱定律的时候，情况就不一样了。

其核心内容如下：一个线性变换(用矩阵乘法表示)可表示为它的所有的特征向量的一个线性组合，其中的线性系数就是每一个向量对应的特征值，写成公式就是：

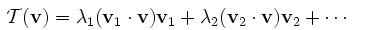
从这里我们可以看出，一个变换(矩阵)可由它的所有特征向量完全表示，而每一个向量所对应的特征值，就代表了矩阵在这一向量上的贡献率—说通俗一点就是能量，特征值掌握了对特征向量的主动：你所能够代表这个矩阵的能量高低掌握在我手中。

一个空间坐标系也可视作一个矩阵，而这个坐标系就可由这个矩阵的所有特征向量表示，可以想象就是一个空间张开的各个坐标角度，这一组向量可以完全表示一个矩阵表示的空间的“特征”，而他们的特征值就表示了各个角度上的能量(可以想象成从各个角度上伸出的长短)。

---