【矩阵论】3.矩阵分解

3 矩阵分解

3.1 三角分解（ LU 分解）

定义 3.1.1 给定矩阵 $A\in {\mathbf{R}}^{n\times n}$ , 若存在下三角矩阵 $L\in {\mathbf{R}}^{n\times n}$ 和上三角矩阵 $U\in {\mathbf{R}}^{n\times n}$ 使得 $A=LU$ , 这种分解称为矩阵的一个三角分解，又称 $LU$ 分解。（Gauss消去法，待定系数法 ）

定理 3.1.2 给定矩阵 $A\in {\mathbf{R}}^{n\times n}$ , 存在单位下三角阵 $L\in {\mathbf{R}}^{n\times n}$ 和可逆上三角阵 $U\in {\mathbf{R}}^{n\times n}$, 使得 $A=LU$ 的充分必要条件是 $A$ 的各阶顺序主子阵均不为零.

$\begin{array}{rl}\left|\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1,n-1}\\ a_{21}& a_{22}& ...& a_{2,n-1}\\ ⋮& ⋮& & ⋮\\ a_{n-1,1}& a_{n-1,2}& ...& a_{n-1,n-1}\end{array}\right|& =\left|\begin{array}{cccc}{a}_{11}^{(1)}& a_{12}^{(1)}& \cdots & a_{1n}^{(1)}\\ & a_{22}^{(2)}& & a_{2n}^{(2)}\\ & & \ddots & ⋮\\ & & & a_{n-1,n-1}^{(n-1)}\end{array}\right|=a_{11}^{(1)}{a}_{22}^{(2)}\cdot \cdot \cdot a_{n-1,n-1}^{(n-1)},\end{array}$

Doolittle 分解

$A=LU$ , $L$ 是单位下三角矩阵，$U$ 是上三角矩阵。在 Gauss 消去过程中有

$\mathbf{A}={\mathbf{L}}_1^{-1}{\mathbf{L}}_2^{-1}\cdot \cdot \cdot {\mathbf{L}}_{n-1}^{-1}{\mathbf{A}}^{(n)}.$ ${\mathbf{L}}_i^{-1}=\left[\begin{array}{cccccc}1& & & & & \\ & \ddots & & & & \\ & & 1& & & \\ & & l_{i+1,i}& 1& & \\ & & \dots & & \ddots & \\ & & l_{n,i}& & & 1\end{array}\right],i=1,2,\cdots ,n-1$

记 $L=L_1^{-1}{L}_2^{-1}...L_{n-1}^{-1}$ 是单位下三角矩阵，$U=A^{(n)}$ 是一个上三角矩阵，则有 $A=LU$ .

Crout 分解 $A=LU$ , 这里 $L$ 是下三角矩阵，$U$ 是单位上三角矩阵.

LDU 分解 $A=LDU$ , 这里 $L$ 是单位下三角矩阵，$D$ 是对角矩阵，$U$ 是单位上三角矩阵.

以上三种分解统称为矩阵的三角分解，或者 $LU$ 分解。如果不作特殊说明，一般所说的 $LU$ 分解就是指 Doolittle 三角分解。实际上，尽管矩阵的三角分解不唯一，但是矩阵的这三种三角分解具有唯一性。

定理 3.1.3 若 $A$ 为 $n$ 阶矩阵，且所有顺序主子式均不等于零，则 $A$ 可分解为一个单位下三角矩阵 $L$ 与一个上三角矩阵 $U$ 的乘积，即 $A=LU$ ，且分解是唯一的. ( $L_2^{-1}{L}_1=U_2{U}_1^{-1}=E$ )

定理 3.1.4 如果矩阵 $A$ 的所有顺序主子式均不等于零，则
(1) $A$ 有唯一的三角分解 $:A=LDU$ ；(2) $A$ 有唯一的 Crout 分解$:A=LU$ 。

Cholesky 分解(对称正定矩阵)

当 $A$ 为对称正定矩阵时，它的所有顺序主子式都大于零，故由定理3.4可知存在唯一的 $LDU$ 分解. 由于对称正定的特殊性，可以得到一个性质更好的三角分解. （待定系数法 求 Cholesky 分解）

定理 3.1.5 若 $A\in {\mathbf{R}}^{n\times n}$ 为对称正定矩阵，则存在唯一的对角元素均为正的下三角矩阵 $G$ , 使得 $A=G{G}^{\mathrm{T}}$ , 这样的分解称为对称正定矩阵的 Cholesky 分解.

证明 根据定理3.4，由 $A$ 是对称正定矩阵，存在唯一的 $LDU$ 分解，即 $A=LDU$。其中 $L$ 是单位下三角矩阵，$D$ 是非奇异的对角矩阵，$U$ 是单位上三角矩阵，
由 $A$ 的对称性可得 $LDU=U^{\mathrm{T}}D{L}^{\mathrm{T}}$ ，按照分解的唯一性可得 $L=U^{\mathrm{T}}$ , 从而 $A=$ $\mathbf{LD}{\mathbf{L}}^{\mathbf{T}}.$
设 $\mathbf{D}=\mathrm{diag}(d_1,d_2,...,d_n),d_i\ne 0,i=1,2,...,n.$ 下证 $D$ 的对角元素均为正，即 $d_i>0.$
由于 $L$ 是单位下三角矩阵，所以 $L^{\mathrm{T}}$ 是单位上三角矩阵，当然也是非奇异矩阵。故对单位坐标向量$e_i=(0,...,0,1,0,...,0{)}^T$ , 存在非零向量 $x_i$ , 使得 $L^{\mathrm{T}}{x}_i=e_i,i=1,2,\cdots ,n.$
$$x_i^{\mathrm{T}}A{x}_i=x_i^{\mathrm{T}}(LD{L}^{\mathrm{T}})x_i=(L^{\mathrm{T}}{x}_i{)}^{\mathrm{T}}D(L^{\mathrm{T}}{x}_i)=e_i^{\mathrm{T}}D{e}_i=d_i.$$由 $x_i^{\mathrm{T}}A{x}_i>0$ , 从而 $d_i>0,i=1,2,...,n$ . 这就证明了 $D$ 的对角元素都为正。
记 ${\mathbf{D}}^{1/2}=\mathrm{diag}(\sqrt{d_1},\sqrt{d_2},\cdots ,\sqrt{d_n})$ ，则有
$$\mathbf{A}={\mathbf{LDL}}^{\mathrm{T}}={\mathbf{LD}}^{1/2}{\mathbf{D}}^{1/2}{\mathbf{L}}^{\mathrm{T}}=({\mathbf{LD}}^{1/2})({\mathbf{LD}}^{1/2}{)}^{\mathrm{T}}.$$记 $G=L{D}^{1/2}$ , 则有 $A=G{G}^{\mathrm{T}}$ ，其中 $L$ 是对角元大于零的下三角矩阵. 易证这个三角分解也是唯一的。

3.2 正交三角分解（QR分解）

首先回顾一下正交矩阵的概念和性质。
定义 3.2.1 若矩阵 $Q\in {\mathbf{R}}^{n\times n}$ , 且满足 $Q{Q}^{\mathrm{T}}=Q^{\mathrm{T}}Q=E$ , 就称矩阵 $Q$ 为正交矩阵。
正交矩阵的性质：$(1)Q^{-1}=Q^{\mathrm{T}};$$(2)\det (Q)=\pm 1;$ $(3)Qx$ 的长度与 $x$ 的长度相等.
下面介绍几类特殊的正交矩阵.

1. 单位矩阵 $E$ 和 置换矩阵 $P_{ij}$ (将单位矩阵的任意两行(列)交换得到的矩阵)
   任意个置换矩阵的乘积仍然是置换矩阵.
2. 旋转矩阵 $\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$ 。二维平面中的一个向量用极坐标表示为 $w=(r\cos \varphi$, $r\sin \varphi {)}^{\mathrm{T}}$，那么$$Gw=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left(\genfrac{}{}{0ex}{}{r\cos \varphi }{r\sin \varphi }\right)=\left(\genfrac{}{}{0ex}{}{r\cos (\theta +\varphi )}{r\sin (\theta +\varphi )}\right),$$即 $Gw$ 表示 将向量 $w$ 逆时针旋转 $\theta$ 角所得到的向量.
   推广到 $n\times n$ 的情形，形如 $$\begin{gathered} G(i,j,\theta )=\left[\begin{array}{ccccccc}1& & & & & & \\ & \ddots & & & & & \\ & & \cos \theta & & \sin \theta & & \\ & & & \ddots & & & \\ & & -\sin \theta & & \cos \theta & & \\ & & & & & \ddots & \\ & & & & & & 1\end{array}\right]{ \\ }_j^i \end{gathered}$$
   的矩阵称为 Givens 矩阵 或 Givens 变换，或称(平面)旋转矩阵(旋转变换)，其中 $\theta$ 为旋转的角度 . 显然，$G(i,j,\theta )$也是正交矩阵.
3. 反射矩阵( Householder 变换) 设 $w\in {\mathbb{R}}^n$ , 且 $\Vert w{\Vert }_2=1$ , 则 $$P=I-2w{w}^{\mathrm{T}}$$ 称为 Householder 变换，或者 Householder 矩阵. Householder 矩阵有如下性质：
   (1) $P^{\mathrm{T}}=P$ , 即 $P$ 是对称阵；
   (2) $P{P}^T=P^2=I-2w{w}^T-2w{w}^T+4w(w^{T}w)w^T=I$ , 即 $P$ 是正交阵，
   (3) 如图 3-1 所示，设 $w$ 是 ${\mathbf{R}}^3$ 上的一个单位向量，并设 $S$ 为过原点且与 $w$ 垂直的平面，则一切 $v\in {\mathbf{R}}^3$ 可分解成 $v=v_1+v_2$ , 其中 $v_1\in S,v_2\perp S.$ 不难验证 $P{v}_1=v_1$，$P{v}_2=-v_2$，所以 $Pv=v_1-v_2$ .
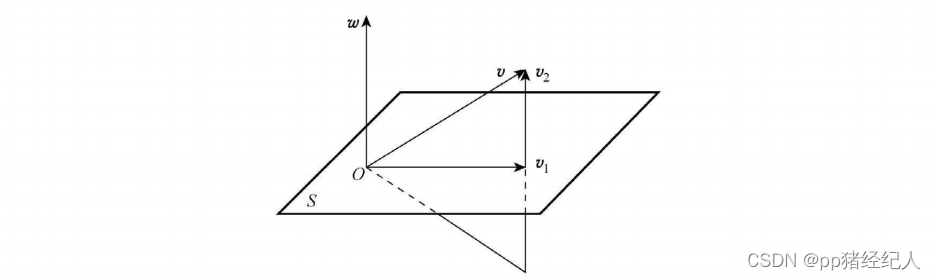
   这样，$v$ 经变换后的象 $Pv$ 是 $v$ 关于 S 对称的向量 . 所以，Householder 变换(图 3-1)又称镜面反射变换，Householder 矩阵也称初等反射矩阵.
     ~  
   应用：对 $x\ne 0$ , 求 Householder 矩阵 $P$ , 使得 $Px=k{e}_1$.
   其中 $e_1=(1,0,...,0{)}^{\mathrm{T}}.$ 由正交矩阵的性质可知 $\parallel Px{\parallel }_2=\parallel k{e}_1{\parallel }_2=\parallel x{\parallel }_2$ , 即 $k=$ $\pm \parallel x{\parallel }_2$ . 由上面所讨论的 $P$ 的构造，有$$u=x-k{e}_1,w=\frac{u}{\parallel u{\parallel }_2}.$$设 $x=(x_1,...,x_n{)}^{\mathrm{T}}$ , 为了使 $x-k{e}_1$ 计算时不损失有效数位(一正一负可能消掉)，取
   $$k=-\mathrm{sign}(x_1)\parallel x{\parallel }_2,\mathrm{sign}(x_1)=\{\begin{array}{ll}1,& \text{当}{x}_1⩾0,\\ -1,& \text{当}{x}_1<0,\end{array}$$ 则 $\mathbf{u}=(x_1+\mathrm{sign}(x_1)\parallel \mathbf{x}{\parallel }_2,x_2,\cdots ,x_n{)}^{\mathrm{T}}$，从而 $P=I-\beta u{u}^{\mathrm{T}}$ ，其中
   $$\beta =2(\parallel \mathbf{u}{\parallel }_2^2{)}^{-1}=2(\parallel \mathbf{x}{\parallel }_2(\parallel \mathbf{x}{\parallel }_2+|x_1|){)}^{-1}.$$

定义 3.2.1 给定矩阵 $A\in {\mathbf{R}}^{n\times n}$ , 若存在 正交矩阵 $Q\in {\mathbf{R}}^{n\times n}$ 和 上三角矩阵 $R\in {\mathbf{R}}^{n\times n}$ 使得 $A=QR$ , 这种分解称为矩阵的一个正交三角分解，又称 $QR$ 分解 .

定理 3.2.2 设 $A\in {\mathbf{R}}^{n\times n}$ , 则存在正交阵 $Q$ , 使得 $A=QR$ , 其中 $R$ 为上三角阵 .

证明 构造性证明 . 首先，考虑 $A$ 的第一列 $a_1=(a_{11},a_{21},...,a_{n1}{)}^T$ , 可找到 Householder 矩阵 $P_1$ , 使得 $P_1{a}_1$ 的元素除了第 1 个以外都为零. 同理，找到 $P_2$ 使得 $P_2{P}_{1}A$ 的第 2 列对角元以下元素为零，而第一列对角元以下元素与 $P_1\mathbf{A}$ 一样是零.依次这样下去，可以得到 $P_{n-1}{P}_{n-2}...P_{1}A=R,$ 其中 $R$ 为上三角矩阵，$Q^{\mathrm{T}}=P_{n-1}{P}_{n-2}...P_1$ 为正交阵，定理证毕.

该定理保证了 $A$ 可分解为 $A=QR$ , 若 $A$ 非奇异，则 $R$ 也非奇异 . 如果不规定 $R$ 的对角元为正，则分解不是唯一的.

定理 3.2.3 设 $A\in {\mathbf{R}}^{n\times n}$ , 且 $A$ 非奇异，则存在正交阵 $Q$ 与上三角阵 $R$ , 使得 $A=QR,$ 且当 $R$ 的对角元均为正时，分解是唯一的.

另外，注意到 $A^{\mathrm{T}}A=(QR{)}^{\mathrm{T}}QR=R^{\mathrm{T}}{Q}^{\mathrm{T}}QR=R^{\mathrm{T}}R$，所以，矩阵 $A$ 正交三角分解中的 $R$ 恰好是矩阵$A^{\mathrm{T}}A$ 的 Cholesky 分解中的上三角矩阵.

除了用 Householder 变换和 Givens 变换，还可以用 Gram-Schmidt 正交化 过程 计算矩阵 A 的正交三角分解.
设有3个 $n$ 阶向量${\alpha }_1,{\alpha }_2,{\alpha }_3$线性无关，令

$\begin{array}{rl}& {\beta }_1={\alpha }_1\\ & {\beta }_2={\alpha }_2-\frac{({\alpha }_2,{\beta }_1)}{|{\beta }_1{|}^2}{\beta }_1\\ & {\beta }_3={\alpha }_3-\frac{({\alpha }_3,{\beta }_2)}{|{\beta }_2{|}^2}{\beta }_2-\frac{({\alpha }_3,{\beta }_1)}{|{\beta }_1{|}^2}{\beta }_1\end{array}$
用 Schmidt 正交化方法可构造 $Q=(\frac{{\beta }_1}{|{\beta }_1|},\frac{{\beta }_2}{|{\beta }_2|},\frac{{\beta }_3}{|{\beta }_3|})$ , 可知 $Q^{H}Q=I$ 。而 $R=Q^{H}A$ 。

3.3 满秩分解

如果矩阵 $\mathbf{A}$ 的行(列)向量组线性无关，则称 $A$ 为行(列)满秩矩阵.

定理 3.3.1 设 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ 且 r a n k ( A ) = r ⩽ min ⁡ { m , n } \mathrm{rank}(\mathbf A)=r\leqslant\min\{m,n\} rank(A)=r⩽min{m,n} , 则可将 $\mathbf{A}$ 作满秩分解 $$\mathbf{A}=\mathbf{CD}$$其中，$\mathbf{C}\in {\mathbb{R}}^{m\times r},\mathbf{D}\in {\mathbb{R}}^{r\times n}$, 且 $\mathrm{rank}(\mathbf{C})=\mathrm{rank}(\mathbf{D})=r.$

证明 因为 $\mathrm{rank}(\mathbf{A})=r$ , 所以存在 $m$ 阶可逆阵 $P$ 和 $n$ 阶置换阵 $Q$ , 使得 $A=P\left(\begin{array}{cc}{\mathbf{E}}_r& \mathbf{O}\\ \mathbf{O}& \mathbf{O}\end{array}\right)Q^{\mathrm{T}}.$
令 $P=(P_1,P_2)$ , 其中 $P_1$ 是 $m\times r$ 列满秩阵，这样
$$\mathbf{A}=({\mathbf{P}}_1,{\mathbf{P}}_2)\left(\begin{array}{cc}{\mathbf{E}}_r& \mathbf{O}\\ \mathbf{O}& \mathbf{O}\end{array}\right){\mathbf{Q}}^{\mathrm{T}}=({\mathbf{P}}_1,\mathbf{O}){\mathbf{Q}}^{\mathrm{T}}={\mathbf{P}}_1({\mathbf{E}}_r,\mathbf{O}){\mathbf{Q}}^{\mathrm{T}},$$显然，($E_r,B)Q^{\mathrm{T}}$ 是行满秩的 $r\times n$ 阵 . 令 $\mathbf{C}={\mathbf{P}}_1,\mathbf{D}=({\mathbf{E}}_r,\mathbf{B}){\mathbf{Q}}^{\mathrm{T}}$ , 即得所证。

设 $C=(c_1,c_2,\cdots ,c_r),D=(d_1,d_2,\cdots ,d_r)$ , 则 $\mathbf{A}=(c_1,c_2,\cdots ,c_r)\left(\begin{array}{c}{d}_1^{\mathrm{T}}\\ d_2^{\mathrm{T}}\\ ⋮\\ d_r^{\mathrm{T}}\end{array}\right)={\sum }_{i=1}^r{c}_i{d}_i^{\mathrm{T}},$
这也是 $\mathbf{A}$ 的满秩分解的一种表示形式.

例 3.3.2 $\begin{array}{rl}& A=({\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,{\mathbf{\alpha }}_3,{\mathbf{\alpha }}_4,{\mathbf{\alpha }}_5)=\left[\begin{array}{ccccc}2& 1& 6& 1& 0\\ 3& 2& 10& 1& 0\\ 2& 3& 10& -1& 3\\ 4& 4& 16& 0& 1\end{array}\right]\end{array}$，求矩阵 $A$ 的满秩分解 .
解 先用行初等变换把矩阵 $A$ 化为简化阶梯形 $\left|\begin{array}{ccccc}1& 0& 2& 1& 0\\ 0& 1& 2& -1& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0\end{array}\right|=({\mathbf{\beta }}_1,{\mathbf{\beta }}_2,{\mathbf{\beta }}_3,{\mathbf{\beta }}_4,{\mathbf{\beta }}_5)=\left(\begin{array}{c}\mathbf{D}\\ \mathbf{O}\end{array}\right)$ , 其中，$\mathbf{D}=\left[\begin{array}{ccccc}1& 0& 2& 1& 0\\ 0& 1& 2& -1& 0\\ 0& 0& 0& 0& 1\end{array}\right]$是 $3\times 5$ 行满秩阵.显然 ${\beta }_1,{\beta }_2,{\beta }_5$ 线性无关，且 $p_3=2{\mathbf{\beta }}_1+2{\mathbf{\beta }}_2,{\mathbf{\beta }}_4={\mathbf{\beta }}_1-{\mathbf{\beta }}_2$ .由于行初等变换保持矩阵列向量组的线性组合关系，因此 ${\alpha }_1,{\alpha }_2,{\alpha }_5$ 线性无关，且${\mathbf{\alpha }}_3=2{\mathbf{\alpha }}_1+2{\mathbf{\alpha }}_2,{\mathbf{\alpha }}_4={\mathbf{\alpha }}_1-{\mathbf{\alpha }}_2$. 取 $\mathbf{C}=({\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,{\mathbf{\alpha }}_5)=\left|\begin{array}{ccc}2& 1& 0\\ 3& 2& 0\\ 2& 3& 3\\ 4& 4& 1\end{array}\right|$, 显然 $C$ 是 $4\times 3$ 列满秩阵，
且满足$\begin{array}{rl}\mathbf{CD}& =({\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,{\mathbf{\alpha }}_5)\left[\begin{array}{ccccc}1& 0& 2& 1& 0\\ 0& 1& 2& -1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\\ & =({\alpha }_1,{\alpha }_2,2{\alpha }_1+2{\alpha }_2,{\alpha }_1-{\alpha }_2,{\alpha }_5)\\ & =({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5)\\ & =\mathbf{A}\end{array}$

进一步有
定理 3.3.3 (正交满秩分解定理) 设 $\mathbf{A}$ 是 $m\times n$ 阶实矩阵，$\mathbf{A}$ 的秩为 $r$ , 则存在 $m\times r$ 列正交矩阵 $\mathbf{Q}$ 和行满秩的 $r\times n$ 阵 $\mathbf{R}$ , 使 $\mathbf{A}=\mathbf{QR}$ . 其中，$\mathbf{Q}$ 列正交的含义为 ${\mathbf{Q}}^{\mathrm{T}}\mathbf{Q}={\mathbf{E}}_{\mathbf{r}}.$

证明 由定理 3.3.1 知存在列满秩的 $m\times r$ 阵 $\mathbf{C}$ 和行满秩的 $r\times n$ 阵 $\mathbf{D}$ , 使 $\mathbf{A}=\mathbf{CD}$ .
于是 ${\mathbf{C}}^{\mathrm{T}}\mathbf{C}$ 是秩为 $r$ 的 $r$ 阶对称方阵，且易证 ${\mathbf{C}}^{\mathrm{T}}\mathbf{C}$ 是正定阵，这样存在 $r$ 阶对称正定阵 $\mathbf{S}$ , 使 ${\mathbf{C}}^{\mathrm{T}}\mathbf{C}={\mathbf{S}}^2$ ,
且 $(\mathbf{C}{\mathbf{S}}^{-1}{)}^{\mathrm{T}}(\mathbf{C}{\mathbf{S}}^{-1})={\mathbf{S}}^{-1}{\mathbf{C}}^{\mathrm{T}}\mathbf{C}{\mathbf{S}}^{-1}={\mathbf{S}}^{-1}{\mathbf{S}}^2{\mathbf{S}}^{-1}={\mathbf{E}}_{\mathbf{r}}.$
记 $\mathbf{Q}=\mathbf{C}{\mathbf{S}}^{-1},\mathbf{R}=\mathbf{SD}$ , 则 $\mathbf{Q}$ 是 $m\times r$ 列正交阵且 $\mathbf{R}$ 是行满秩的 $r\times n$ 阵，显然有$$\mathbf{QR}=\mathbf{C}{\mathbf{S}}^{-1}\mathbf{SD}=\mathbf{CD}=\mathbf{A}.$$

3.4 谱分解

矩阵的谱分解仅对某一类特殊的矩阵讨论。通常将可以酉对角化的矩阵称为正规矩阵，即有下面的定义.

定义 3.4.1 设矩阵 $\mathbf{A}\in {\mathbb{C}}^{n\times n}$ , 若 $\mathbf{A}{\mathbf{A}}^{\mathrm{H}}={\mathbf{A}}^{\mathrm{H}}\mathbf{A}$ , 则称 $\mathbf{A}$ 为 正规矩阵.

实对称矩阵、实反对称矩阵、正交矩阵、Hermite 矩阵、反 Hermite 矩阵、西矩阵都是正规矩阵。另外，若 $\mathbf{A}$ 为正规矩阵，则与 $\mathbf{A}$ 酉相似的矩阵仍为正规矩阵.

正规矩阵具有许多好的数学特性.

定理 3.4.2 设矩阵 $\mathbf{A}\in {\mathbb{C}}^{n\times n}$ ,则 $\mathbf{A}$ 是正规矩阵当且仅当 $\mathbf{A}$ 有 $n$ 个两两正交的单位特征向量。

证 首先 $AX={\lambda }_{1}X$ 可得 $A^{H}X={\overline{\lambda }}_{1}X$.
引理1：$AX=0\iff ||AX||=0\iff X^{H}A{A}^{H}X=0\iff A^{H}X=0$
引理2：若$A$ 正规 $AX=\lambda X\Rightarrow A^{H}X=\overline{\lambda }X$
        ~~~~~~~        只 需 证 $(A-\lambda I{)}^{H}X=0$,
        ~~~~~~~         由 $(A-\lambda I)X=0\Rightarrow {\left((A-\lambda I)X\right)}^H(A-\lambda I)X=0\Rightarrow X^H(A-\lambda I{)}^H(A-\lambda I)X=0$
        ~~~~~~~         由于 $A-\lambda I$ 正规，$(A-\lambda I{)}^H(A-\lambda I)=(A-\lambda I)(A-\lambda I{)}^H$
        ~~~~~~~         即有 $X^H((A-\lambda I{)}^H{)}^H(A-\lambda I{)}^{H}X=0$
        ~~~~~~~         $\Rightarrow ((A-\lambda I{)}^{H}X{)}^H(A-\lambda I{)}^{H}X=|(A-\lambda I{)}^{H}X{|}^2=0$
        ~~~~~~~         $\Rightarrow (A-\lambda I{)}^{H}X=0\Rightarrow (A^H-\overline{\lambda }I)X=0\Rightarrow A^{H}X=\overline{\lambda }X$
        ~~~~~~~         故结论得证，若 $A$ 正规，则 $AX=\lambda X⟺A^{H}X=\overline{\lambda }X$
        ~~~~~~~         其中，若 λ ( A ) = { λ 1 , ⋯   , λ n } \lambda(A)=\{\lambda_1,\cdots,\lambda_n\} λ(A)={λ1​,⋯,λn​},则 λ ( A H ) = { λ 1 ‾ , ⋯   , λ n ‾ } \lambda(A^H)=\{\overline{\lambda_1},\cdots,\overline{\lambda_n}\} λ(AH)={λ1​​,⋯,λn​​}
下证 $Ax={\lambda }_{1}x,Ay={\lambda }_{2}y$，$x^{H}y=0$
$y^{H}Ax=y^H{\lambda }_{1}x={\lambda }_1{y}^{H}x$
$=(A^{H}y{)}^{H}x$ $=({\overline{\lambda }}_{2}y{)}^{H}x$ $=({\overline{\lambda }}_{2}y{)}^{H}x$
$={\lambda }_2{y}^{H}x$

定理 3.4.3 设矩阵 $\mathbf{A}=(a_{ij}{)}_{n\times n}\in {\mathbb{C}}^{n\times n},{\lambda }_1,{\lambda }_2,...,{\lambda }_n$为 $\hat{\mathbf{A}}$ 的 $n$ 个特征值，则 $\mathbf{A}$ 是正规矩阵 当且仅当 ${\sum }_{i=1}^n\mid {\lambda }_i{\mid }^2={\sum }_{i,j=1}^n\mid a_{ij}{\mid }^2$ .

定义 3.4.5 给定矩阵 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ 是一个正规矩阵，若存在可逆矩阵 $\mathbf{P}\in {\mathbb{R}}^{n\times n}$ 和对角矩阵 Λ = diag ⁡ { λ 1 , λ 2 , ⋯   , λ n } ∈ R n × n \boldsymbol{\Lambda}=\operatorname{diag}\{\lambda_1,\lambda_2,\cdots,\lambda_n\}\in\mathbf{R}^{n\times n} Λ=diag{λ1​,λ2​,⋯,λn​}∈Rn×n 使得
$$A=P\Lambda P^{-1},$$

这种分解称为矩阵 $\mathbf{A}$ 的一个谱分解. 其中，特征值 { λ 1 , λ 2 , ⋯   , λ n } \{\lambda_1,\lambda_2,\cdots,\lambda_n\} {λ1​,λ2​,⋯,λn​} 也称为矩阵 $\mathbf{A}$ 的谱.

设 $\mathbf{P}=({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n),{\mathbf{P}}^{-1}=({\mathbf{\beta }}_1,{\mathbf{\beta }}_2,\cdots ,{\mathbf{\beta }}_n{)}^{\mathrm{T}}$ ,
则 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n$ 线无， ${\mathbf{\beta }}_1,{\mathbf{\beta }}_2,\cdots ,{\mathbf{\beta }}_n$也线无，且 $A{\mathbf{\alpha }}_i={\lambda }_i{\mathbf{\alpha }}_i,A^{\mathrm{T}}{\mathbf{\beta }}_i={\lambda }_i{\mathbf{\beta }}_i(1⩽i⩽n,$ 这样$\begin{array}{rl}\mathbf{A}& =\mathbf{P}\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right){\mathbf{P}}^{-1}=({\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,\cdots ,{\mathbf{\alpha }}_n)\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]\left(\begin{array}{c}{\mathbf{\beta }}_1^{\mathrm{T}}\\ {\mathbf{\beta }}_2^{\mathrm{T}}\\ ⋮\\ {\mathbf{\beta }}_n^{\mathrm{T}}\end{array}\right)\\ & =\sum _{k=1}^n{\lambda }_i{\mathbf{\alpha }}_i{\mathbf{\beta }}_i^{\mathrm{T}}.\end{array}$
这是矩阵 $\mathbf{A}$ 的谱分解的另一种表达形式. 如果记 ${\mathbf{A}}_{\mathbf{i}}={\mathbf{\alpha }}_{\mathbf{i}}{\mathbf{\beta }}_{\mathbf{i}}^{\mathrm{T}}$ , 则可写成 $\mathbf{A}={\sum }_{k=1}^n{\lambda }_i{\mathbf{A}}_i.$

其中，${\mathbf{A}}_i$ 有性质：(1) ${\mathbf{A}}_{\mathbf{i}}^2={\mathbf{A}}_{\mathbf{i}}(i=1,2,\cdots ,n);$ (2) ${\mathbf{A}}_i{\mathbf{A}}_j=\mathbf{O}(i\ne j);$ (3) ${\sum }_{i=1}^n{\mathbf{A}}_{\mathbf{i}}=\mathbf{E}.$

$\begin{array}{c}\mathbf{P}=({\mathbf{\alpha }}_1,{\mathbf{\alpha }}_2,\cdots ,{\mathbf{\alpha }}_n),{\mathbf{P}}^{-1}=\left[\begin{array}{c}{\mathbf{\beta }}_1^{\mathrm{T}}\\ {\mathbf{\beta }}_2^{\mathrm{T}}\\ ⋮\\ {\mathbf{\beta }}_n^{\mathrm{T}}\end{array}\right],\text{则}{\mathbf{P}}^{-1}\mathbf{P}=\left[\begin{array}{ccc}{\mathbf{\beta }}_1^{\mathrm{T}}{\mathbf{\alpha }}_1& \cdots & {\mathbf{\beta }}_1^{\mathrm{T}}{\mathbf{\alpha }}_n\\ ⋮& & ⋮\\ {\mathbf{\beta }}_n^{\mathrm{T}}{\mathbf{\alpha }}_1& \cdots & {\mathbf{\beta }}_n^{\mathrm{T}}{\mathbf{\alpha }}_n\end{array}\right]=\mathbf{E},\\ \mathbf{P}{\mathbf{P}}^{-1}={\mathbf{\alpha }}_1{\mathbf{\beta }}_1^{\mathrm{T}}+\cdots +{\mathbf{\alpha }}_n{\mathbf{\beta }}_n^{\mathrm{T}}=\mathbf{E}.\text{于是}{\mathbf{\beta }}_{\mathbf{i}}^{\mathrm{T}}{\mathbf{\alpha }}_{\mathbf{i}}=1,{\mathbf{\beta }}_{\mathbf{i}}^{\mathrm{T}}{\mathbf{\alpha }}_{\mathbf{j}}=0(i\ne j),\sum _{k=1}^n{\mathbf{\alpha }}_{\mathbf{i}}{\mathbf{\beta }}_{\mathbf{i}}^{\mathrm{T}}=\mathbf{E}.\\ \text{再结合 }{\mathbf{A}}_i={\mathbf{\alpha }}_i{\mathbf{\beta }}_i^{\mathrm{T}}\text{ 就得到上面三个性质}.\end{array}$

例 3.4.6 设 $\mathbf{A}=\left[\begin{array}{ccc}4& -6& 0\\ 2& -3& 0\\ -2& 3& 2\end{array}\right]$ , 求 $\mathbf{A}$ 的谱分解.

先求 $\mathbf{A}$ 的特征值和特征向量. $\mid \lambda E-A\mid =$ $=\lambda (\lambda -2)\left(\lambda -1\right)$ , 因此，$\mathbf{A}$ 有3个不同的特征值 ${\lambda }_1=0,{\lambda }_2=1,{\lambda }_3=2$ , 故 $\mathbf{A}$ 可对角化，从而 $\mathbf{A}$ 的谱分解一定存在.容易求出它们对应的特征向量为
$$p_1=(3,2,0{)}^{\mathrm{T}},p_2=(2,1,1{)}^{\mathrm{T}},p_3=(0,0,1{)}^{\mathrm{T}}.$$令 $\mathbf{P}=(p_1,p_2,p_3)=\left[\begin{array}{ccc}3& 2& 0\\ 2& 1& 0\\ 0& 1& 1\end{array}\right]$ ，显然 , $P$ 可逆,且易求得 ${\mathbf{P}}^{-1}=\left(\begin{array}{c}{\mathbf{\beta }}_1^{\mathrm{T}}\\ {\mathbf{\beta }}_2^{\mathrm{T}}\\ {\mathbf{\beta }}_3^{\mathrm{T}}\end{array}\right)=\left(\begin{array}{ccc}-1& 2& 0\\ 2& -3& 0\\ -2& 3& 1\end{array}\right)$。
这样有
$\begin{array}{rl}& \mathbf{A}=\mathbf{P}\left(\begin{array}{ccc}0& & \\ & 1& \\ & & 2\end{array}\right){\mathbf{P}}^{-1}=({\mathbf{p}}_1,{\mathbf{p}}_2,{\mathbf{p}}_3)\left(\begin{array}{ccc}0& & \\ & 1& \\ & & 2\end{array}\right)\left(\begin{array}{c}{\mathbf{\beta }}_1^{\mathrm{T}}\\ {\mathbf{\beta }}_2^{\mathrm{T}}\\ {\mathbf{\beta }}_3^{\mathrm{T}}\end{array}\right)=p_2{\beta }_2^{\mathrm{T}}+2p_3{\beta }_3^{\mathrm{T}},\end{array}$

3.5 奇异值分解

前面已知，正规矩阵可以酉对角化，因此其对应的线性变换具有很好的性质 . 现考虑 非正规矩阵.

定义3.5.1 设 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ , 半正定矩阵 ${\mathbf{A}}^{\mathrm{T}}\mathbf{A}$ 的 $n$ 个特征值记为 ${\lambda }_i,i=1,2,...,n$ , 显然 ${\lambda }_i⩾0$ . 称 ${\lambda }_i$ 的算术平方根 ${\sigma }_i=\sqrt{{\lambda }_i}$ ($i=1,2,...,n)$为矩阵 $\mathbf{A}$ 的 奇异值.

定理 3.5.2 (奇异值分解定理) 设矩阵 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ 的奇异值中有 $r$ 个不等于零，记为 ${\sigma }_1⩾$ ${\sigma }_2\ge \cdots \ge {\sigma }_r>0.$ 它们构成的 $r$ 阶对角阵记为 D = diag ⁡ { σ 1 , σ 2 , ⋯   , σ r } D=\operatorname{diag}\{\sigma_1,\sigma_2,\cdots,\sigma_r\} D=diag{σ1​,σ2​,⋯,σr​} . 令 $m\times n$ 阶矩阵 $\mathbf{\Sigma }=\left(\genfrac{}{}{0ex}{}{\mathbf{D}\mathbf{O}}{\mathbf{O}\mathbf{O}}\right)$ , 则存在正交矩阵 $\mathbf{U}\in {\mathbb{R}}^{m\times m},\mathbf{V}\in {\mathbb{R}}^{n\times n}$ ,使
$$A=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}.$$

证明 因为 ${\mathbf{A}}^{\mathrm{T}}\mathbf{A}$ 是 $n$ 阶半正定矩阵，必存在 $n$ 阶正交矩阵 $\mathbf{V}$ 使
  ~  
$V^{\mathrm{T}}(A^{\mathrm{T}}A)V=\left[\begin{array}{ccccccc}{\lambda }_1& & & & & & \\ & \ddots & & & & & \\ & & {\lambda }_r& & & & \\ & & & 0& & & \\ & & & & \ddots & & \\ & & & & & 0& \end{array}\right]={\left[\begin{array}{cc}{D}^2& O\\ O& O\end{array}\right]}_{n\times n}$
  ~  
将 $\mathbf{V}$ 分块 $\mathbf{V}=({\mathbf{V}}_1,{\mathbf{V}}_2),$ 其中 ${\mathbf{V}}_1\in {\mathbf{R}}^{n\times r},{\mathbf{V}}_2\in {\mathbf{R}}^{n\times (n-r)}$ .
因为 $\mathbf{V}$ 是正交阵，所以 ${\mathbf{V}}_1^{\mathrm{T}}{\mathbf{V}}_1={\mathbf{E}}_r,{\mathbf{V}}_1^{\mathrm{T}}{\mathbf{V}}_2=\mathbf{O}$, 则$\left[\begin{array}{c}{\mathbf{V}}_1^{\mathrm{T}}\\ {\mathbf{V}}_2^{\mathrm{T}}\end{array}\right]{\mathbf{A}}^{\mathrm{T}}\mathbf{A}({\mathbf{V}}_1,{\mathbf{V}}_2)=\left[\begin{array}{cc}{\mathbf{D}}^2& \mathbf{O}\\ \mathbf{O}& \mathbf{O}\end{array}\right]$
得$\begin{array}{l}{V}_1^T{A}^{T}A{V}_1=D^2,\\ V_2^T{A}^{T}A{V}_2=0,\end{array}$，即 $A{V}_2=0$ .
而 $A=AV{V}^{\mathrm{T}}=A(V_1,V_2)\left(\begin{array}{c}{V}_1^{\mathrm{T}}\\ V_2^{\mathrm{T}}\end{array}\right)=A{V}_1{V}_1^{\mathrm{T}}+A{V}_2{V}_2^{\mathrm{T}}=A{V}_1{V}_1^{\mathrm{T}}=A{V}_1{D}^{-1}D{V}_1^{\mathrm{T}}=U_{1}D{V}_1^{\mathrm{T}}$
  ~  
其中 $U_1=A{V}_1{D}^{-1},U_1\in {\mathbf{R}}^{m\times r}$ , 且 $U_1^{\mathrm{T}}{U}_1=D^{-1}{V}_1^{\mathrm{T}}{A}^{\mathrm{T}}A{V}_1{D}^{-1}=D^{-1}{D}^2{D}^{-1}=E_r$ .
将 $U_1$ 扩张成正交矩阵 $U=(U_1,U_2)$ , 则有
$$\begin{array}{c}\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}=({\mathbf{U}}_1,{\mathbf{U}}_2)\left(\genfrac{}{}{0ex}{}{\mathbf{D}\mathbf{O}}{\mathbf{O}\mathbf{O}}\right)\left(\begin{array}{c}{\mathbf{V}}_1^{\mathrm{T}}\\ {\mathbf{V}}_2^{\mathrm{T}}\end{array}\right)\\ =({\mathbf{U}}_1\mathbf{D},\mathbf{O})\left(\begin{array}{c}{\mathbf{V}}_1^{\mathrm{T}}\\ {\mathbf{V}}_2^{\mathrm{T}}\end{array}\right)\\ ={\mathbf{U}}_1\mathbf{D}{\mathbf{V}}_1^{\mathrm{T}}=\mathbf{A}.\end{array}$$