在做数值计算后处理中,需要对计算模型的边界数据进行坐标旋转,网上找到的公式大多是以原点为旋转中心点。因此这里直接考虑旋转中心点为一般坐标点的情况,将该部分内容作简单推导和整理。

如上图所示,以点M (a,b)为圆心将点N0(x0,y0)旋转到N1(x1,y1)。点N0与水平轴的夹角为α,从点N0到N1的旋转角度为β,角度均已逆时针方向为正,顺时针方向为负。根据三角形内边角关系有,
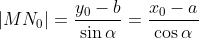
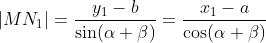
由
在做数值计算后处理中,需要对计算模型的边界数据进行坐标旋转,网上找到的公式大多是以原点为旋转中心点。因此这里直接考虑旋转中心点为一般坐标点的情况,将该部分内容作简单推导和整理。

如上图所示,以点M (a,b)为圆心将点N0(x0,y0)旋转到N1(x1,y1)。点N0与水平轴的夹角为α,从点N0到N1的旋转角度为β,角度均已逆时针方向为正,顺时针方向为负。根据三角形内边角关系有,
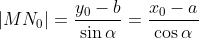
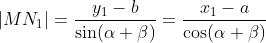
由
 3154
3154
 1258
1258
 550
550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


