CQF笔记M2L1现代资产组合管理理论

Module 2 Quantitative Risk & Return

Lecture 1 Portfolio Management

内容：

• 资产组合管理和理论的核心概念
  • 风险资产和无风险资产
  • 均值方差分析
  • 最优组合
  • 分散化
  • 机会集合(Opportunity set)和有效前沿
  • 切线组合(Tangency portfolio)和市场组合
  • 夏普比例和风险的市场价格
  • 线性模型和CAPM模型
  • 套利定价理论(APT)
  • 风险调整后的业绩度量
• 现代资产组合理论的缺陷：维度和参数估计

2.1.1 MPT

历史

• 1952年马科维茨提出现代资产组合理论(Modern Portfolio Theory, MPT)，将风险和收益放在同等重要的地位：
  • 要获得更高的收益，必须承担更多的风险（风险-收益权衡）
  • 通过分散化投资可以降低风险，同时不会明显降低收益
  • 在马科维茨的框架内，分散化的好处依赖于资产收益的相关性
• 威廉夏普提出CAPM模型，在资产价格和组合选择之间建立一个清晰的关系
• 有几个学者在夏普之前提出CAPM模型，但是未发表
• MPT理论是金融经济学和量化金融的开端

资产组合

$N$ 资产数量($N\ge 2$)
$W$ 资产价值
$T$ 持有年数
$w_i$ 资产权重

可以买入或者卖出（short）资产，在投资期间$T$内持有资产

资产种类 :

• 金融资产：股票、债券、现金
• 实物或可证实的资产(Real assets)：大宗商品、房地产、收藏品、工厂、消费品等
• 无形资产：劳动所得

现实中，组合管理者通常投资单个资产大类和国家

2.1.2 MPT的核心假设

投资的目的（效用）

• 在给定风险下的使收益最大
• 在给定收益目标时的使风险最小

均值-方差

MPT用收益的波动性（标准差）度量风险

$\begin{array}{rl}收益& =(资产/组合)收益的期望\\ 风险& =(资产/组合)收益的标准差\end{array}$

• 资产收益的期望: ${\mu }_i,i=1,\cdots ,N$
• 资产收益的标准差: ${\sigma }_i,i=1,\cdots ,N$
• 两个资产的收益之间的相关性: ${\rho }_{ij},i,j=1,\cdots ,N$

资产收益的分布是椭圆形的(Elliptical)，正态分布和T分布都是椭圆分布。

MPT是均值-方差优化问题

无风险资产

• 收益为R（无风险利率）
• 标准差/波动性为0
• 无风险资产与其他资产的相关性为0

进一步的假设

• 只考虑总收益，也就是所有分红、利率会重新投资
• 无限分割投资(例如可以投资半套房子)
• 投资者能以无风险利率存款和借贷
• 做空有风险资产不受限制
• 市场无摩擦：无税收、无交易费、无须交付抵押品或保证金

2.1.3 简化的例子：无风险资产和两个风险资产组成的投资组合

符号

• ${\mu }_A,{\sigma }_A,{\omega }_A$表示资产A的收益的期望值，收益的方差，权重
• ${\mu }_B,{\sigma }_B,{\omega }_B$表示资产B的收益的期望值，收益的方差，权重
• $R$ 无风险收益
• ${\mu }_{\pi },{\sigma }_{\pi },{\omega }_B$表示资产组合的收益的期望值，收益的方差

无风险资产和一个风险资产的组合（一次函数）

$${\mu }_{\pi }=R+{\sigma }_{\pi }\frac{{\mu }_A-R}{{\sigma }_A}$$

两个风险资产的组合（二次函数）

最小方差组合

有效前沿

上半部分(红色)表示给定风险条件下，期望收益最大
下半部分(黑色)表示给定风险条件下，期望收益最小

两个风险资产的相关性为1（退化为一次函数）

两个风险资产的相关性为-1（退化为一次函数，分为两段，但上半部分是有效的）

零方差（风险）组合

两个相关性为负数的资产可以构建零方差组合

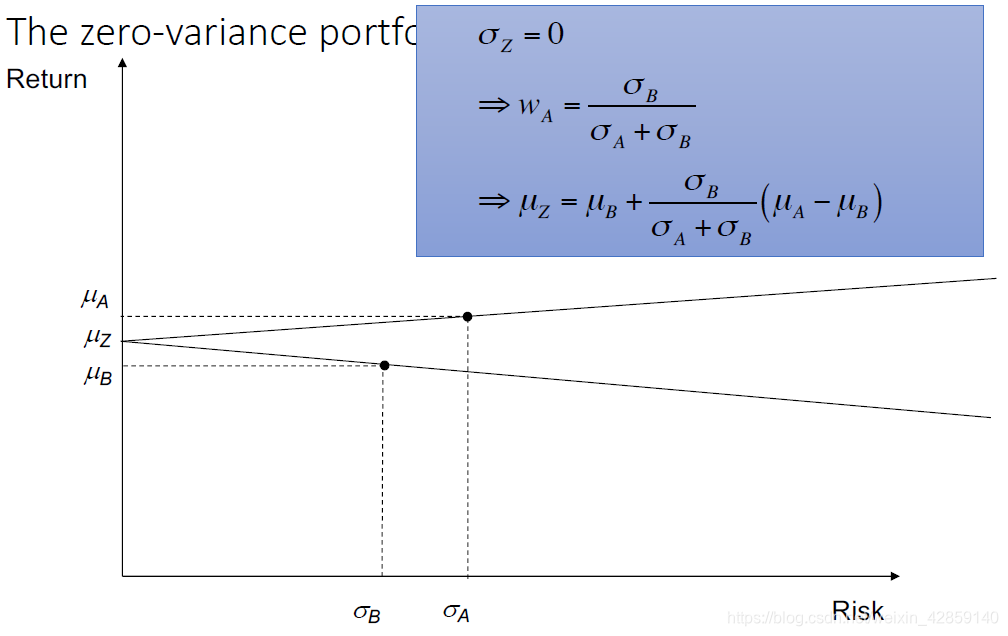
两个资产的相关性为0

不同相关性对应的曲线

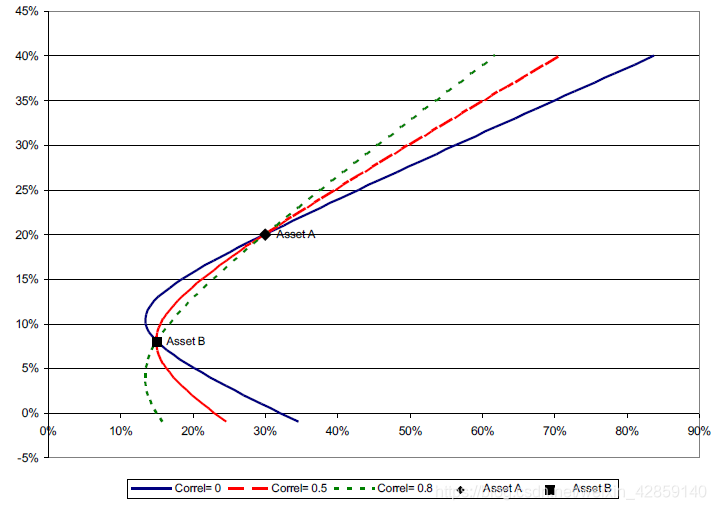
无风险资产和两个风险资产

新的有效前沿

斜率越大，效用越大

切线组合

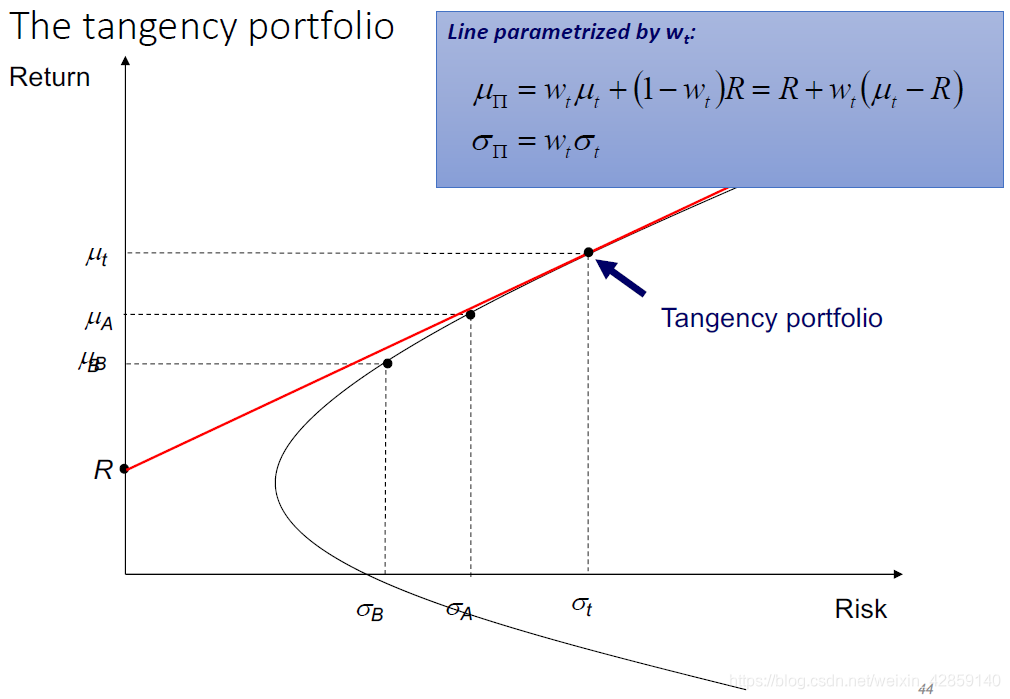
切线组合的资产配置

切合组合的斜率
$$S_t=\frac{{\mu }_t-R}{{\sigma }_t}$$

夏普比率
投资组合C全部由资产C和无风险资产构成
$${\mu }_{\pi }=R+{\sigma }_{\pi }\frac{{\mu }_C-R}{{\sigma }_C}=R+S_C{\sigma }_{\pi }$$

其中
$$S_C=\frac{{\mu }_C-R}{{\sigma }_C}$$

$S_C$称为投资C的夏普比率：

• 表示经过风险调整的超额回报
• 夏普比率越高，投资组合的业绩也好
• 夏普比率最高的风险资产组合是切线组合

相关性${\rho }_{AB}=-1$的情况下（考察零方差组合）

三种情况

• ${\mu }_Z>R$
• ${\mu }_Z<R$
• ${\mu }_Z=R$

前两种情况都可以获得无风险收益（套利）

• ${\mu }_Z>R$：short 无风险资产（收益为$-R$），long 零方差组合（收益为${\mu }_Z$），总收益为${\mu }_Z-R$
• ${\mu }_Z<R$：long 无风险资产（收益为$R$），short 零方差组合（收益为$-{\mu }_Z$），总收益为$R-{\mu }_Z$

套利机会不会长期存在，最后会达到均衡状态${\mu }_Z=R$
这是期权和衍生品定价的基础（无套利定价理论）

2.1.4 无风险资产和N个风险资产

仍然讨论以下几个问题：

• 机会集
• 有效前沿
• 切线组合
• 夏普比率

N个风险资产

权重
$${\omega }_i=\frac{资产i的市值}{组合的总市值}$$

$$\sum _{i=1}^N{\omega }_i=1$$

向量形式
$${\vec{w}}^T{\vec{1}}_N=1$$

组合收益的期望值
$${\mu }_{\pi }:=E[r_{\pi }]=\sum _{i=1}^N{\omega }_i{\mu }_i={\vec{\omega }}^T\vec{\mu }$$

组合收益的标准差
$${\sigma }_{\pi }=\sqrt{{\vec{\omega }}^T\vec{\Sigma }\vec{\omega }}=\sqrt{\sum _{i=1}^N\sum _{j=1}^N{\omega }_i{\omega }_{j}Cov(R_i,R_j)}=\sqrt{\sum _{i=1}^N{\omega }_i^2{\sigma }_i^2+2\sum _{\genfrac{}{}{0ex}{}{i=1}{j>i}}^N{\omega }_i{\omega }_j{\rho }_{ij}{\sigma }_i{\sigma }_j}$$

求解带约束条件的优化问题

1. 给定收益时风险(方差）最小
   $$\underset{{\omega }_1,\cdots ,{\omega }_N}{\min }{\sigma }_{\pi }^2({\omega }_1,\cdots ,{\omega }_N)$$
   约束条件
   $$\begin{gathered} E[{\mu }_{\pi }({\omega }_1,\cdots ,{\omega }_N)]=m \\ \sum _{i=1}^N{\omega }_i=1 \end{gathered}$$

2. 给定风险(方差)时，收益最大：
   $$\underset{{\omega }_1,\cdots ,{\omega }_N}{\min }E[{\mu }_{\pi }({\omega }_1,\cdots ,{\omega }_N)]$$
   约束条件
   $$\begin{gathered} {\sigma }_{\pi }^2({\omega }_1,\cdots ,{\omega }_N)={\nu }^2 \\ \sum _{i=1}^N{\omega }_i=1 \end{gathered}$$

第一种情况（给定收益，最小化方差）目标更清晰，而且更容易求解

构造目标函数
$$\underset{{\omega }_1,\cdots ,{\omega }_N}{\min }E[{\mu }_{\pi }({\omega }_1,\cdots ,{\omega }_N)]-\frac{\lambda }{2}{\sigma }_{\pi }^2({\omega }_1,\cdots ,{\omega }_N)$$
$$\sum _{i=1}^N{\omega }_i=1$$

• $\lambda$用于度量投资者的风险厌恶程度
• $\lambda$作为惩罚因子，$\lambda$越大，（对风险的）惩罚越大

风险资产组合的机会集和有效前沿

分散化

假设：

• 所有资产收益的期望值相同 ${\mu }_i=\mu ,i=1,\cdots ,N$
• 所有资产收益的标准差相同 ${\sigma }_i=\sigma ,i=1,\cdots ,N$
• 所有资产收益的相关系数相同 ${\rho }_{ij}=\rho ,i,j=1,\cdots ,N$
• 所有资产的权重相同 ${\omega }_i=1/N$

组合收益的期望值 $${\mu }_{\pi }=\mu$$

组合收益的标准差
$${\sigma }_{\pi }^2=\sum _{i=1}^N{\omega }_i^2{\sigma }_i^2+\sum _{\genfrac{}{}{0ex}{}{i=1}{j\ne i}}^N{\omega }_i{\omega }_j{\rho }_{ij}{\sigma }_i{\sigma }_j=(\rho +\frac{1-\rho }{N}){\sigma }^2$$

当N变大时 $${\sigma }_{\pi }^2=\rho {\sigma }^2$$

当$\rho =0$时 $${\sigma }_{\pi }^2=\frac{1}{N}{\sigma }^2$$

当资产收益之间的相关性为0时，组合收益的标准差符合平方根法则

• 随着资产数量增加，风险变小
• 组合中的资产数量为30~50个时，分散化收益最大
• 所有市场都有最小风险限制：无论如何分散化，风险不会小于最低风险
  

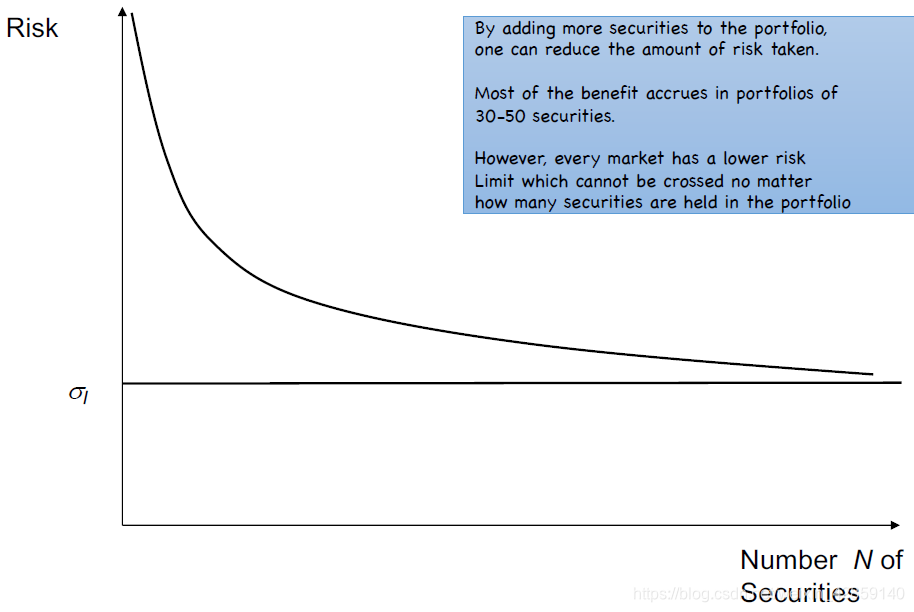
进一步降低风险的方法是在市场之间（多个资产大类或者国家）分散化投资

无风险资产和N个风险资产

无风险资产的权重$${\omega }_0=1-\sum _{i=1}^N{\omega }_i=1-{\vec{\omega }}^T{\vec{1}}_N$$

组合收益的期望值
组合收益的期望值
$${\mu }_{\pi }:=E[r_{\pi }]={\omega }_{0}R+\sum _{i=1}^N{\omega }_i{\mu }_i=R+\sum _{i=1}^N{\omega }_i({\mu }_i-R)=R+{\vec{\omega }}^T(\vec{\mu }-R\vec{1})$$

组合收益的标准差
$${\sigma }_{\pi }=\sqrt{{\vec{\omega }}^T\vec{\Sigma }\vec{\omega }}=\sqrt{\sum _{i=1}^N\sum _{j=1}^N{\omega }_i{\omega }_{j}Cov(R_i,R_j)}=\sqrt{\sum _{i=1}^N{\omega }_i^2{\sigma }_i^2+2\sum _{\genfrac{}{}{0ex}{}{i=1}{j>i}}^N{\omega }_i{\omega }_j{\rho }_{ij}{\sigma }_i{\sigma }_j}$$

Further MPT

• 市场组合和风险的市场价格
• 均值-方差分析的计算效率问题
• 因子模型和资本资产定价模型CAPM
• 多因子模型
  • Ad hoc models
  • 套利定价模型APT
  • Fama-French（三因子/五因子模型）
  • Pastor-Stambaugh
• Beyond MPT: other optimization criteria

市场组合

假设：

• 假设市场中所有投资者：
  • 都投资在无风险资产和N个风险资产上
  • 相同的投资周期T
  • 相同的市场参数（收益的期望值，标准差和相关性）
• 所有投资者投资相同的市场组合
• 所有资产的相对市场价值会反映到其在切线组合中的配置权重
• 切线组合成为底层市场资产的完美代表

这样：

• 切线组合成为市场组合
• 切线成为资本市场线(Capital Market Line, CML)

夏普比率和风险的市场价格

• 市场组合是夏普比率最大的风险资产组合（也就是有效前沿中，斜率最大的点）
• 所有人都投资市场组合和无风险资产，夏普比率被解释为风险的市场价格
• 夏普比率用于测量承担一单位市场风险获得的超额回报
• 在利率模型和债券定价中，也会用到风险的市场价格

实际的市场

• 没有单一的金融指数或者经济时间序列能跟踪所有可交易资产的价格
• 现实中的解决方法是使用“代理(proxy)”：用金融指数（例如S&P 500或MSCI World Index）代表金融市场中大量可交易资产
• 这种方法不完美，因为只能反映可交易资产的一小部分。但是在实际又是可行的，因为多数资产管理者只管理少数几种资产类别

均值-方差分析的计算效率问题

• 均值方差分析的主要问题是维度问题，假设一共N个资产，要计算：
  • N个收益的期望值
  • N个收益的标准差
  • N(N-1)/2的收益的相关系数
• 当N变大时，参数数量按平方增加，也就是$O(N^2)$

线性因子模型

定义

$$r_i={\alpha }_i+{\beta }_i{r}_M+{ϵ}_i$$

$r_i$ 资产$i$在参考周期内的实际收益
${\beta }_i$ 资产收益对市场收益的敏感程度，度量资产$i$对系统风险的敞口
${\alpha }_i$ 反映资产$i$产生的基本收益
${ϵ}_i$ 反映资产$I$自身的风险(idiosyncratic risk)，是与市场风险无关的风险残差项（有关的部分已经用市场风险解释了）。假设$ϵ\sim N(0,e_i^2)$，并且$Cov({ϵ}_i,{ϵ}_j)=0fori\ne j$

当市场组合（或者市场组合的proxy）确定下来之后，可以用线性回归估计参数项。

因子模型的计算效率

• N个$\alpha$
• N个$\beta$
• N个$ϵ$

参数数量为$O(N)$

单个资产C

收益
$$r_C={\alpha }_C+{\beta }_C{r}_M+{ϵ}_C$$

收益的期望值
$${\mu }_C:=E[r_C]={\alpha }_C+{\beta }_C{\mu }_M$$

收益的标准差
$${\sigma }_C=\sqrt{{\beta }_C^2{\sigma }_M^2+e_C^2}$$

收益的协方差
$$Cov(C,D):={\sigma }_{CD}={\beta }_C{\beta }_D{\sigma }_M^2$$

投资组合C：由所有N个风险资产组成

权重 ${\omega }_i,i=1,\cdots ,N$

收益
$$r_C=\sum _{i=1}^N{\omega }_i{\alpha }_i+\sum _{i=1}^N{\omega }_i{\beta }_i{r}_M+\sum _{i=1}^N{\omega }_i{ϵ}_i$$

收益的期望值
$${\mu }_C:=E[r_C]=\sum _{i=1}^N{\omega }_i{\alpha }_i+\sum _{i=1}^N{\omega }_i{\beta }_i{\mu }_M$$

收益的标准差
$${\sigma }_C=\sqrt{(\sum _{i=1}^N{\omega }_i{\beta }_i{)}^2{\sigma }_M^2+\sum _{i=1}^N{\omega }_i^2{e}_i^2}$$

$$e_C^2=\sum _{i=1}^N{\omega }_i^2{e}_i^2$$

分散化收益

假设

• 所有残差项${ϵ}_i$独立同分布(IID), 即
  • ${ϵ}_i\sim N(0,e^2),i=1,\cdots ,N$
  • $Cov({ϵ}_i,{ϵ}_j)=0,i,j=1,\cdots ,N,j\ne j$
• 所有资产权重相等：${\omega }_i=\omega =1/N$
• 所有资产的系统系统风险相同：${\beta }_i=\beta$

$${\sigma }_C=\sqrt{{\beta }^2{\sigma }_M^2+\frac{e^2}{N}}$$

当$N\to \infty$时
$${\sigma }_{\pi }=\beta {\sigma }_M$$

残差项(反映资产自身的风险)消失（反映分散化收益）

CAPM

an ad hoc模型

线性因子模型是一个ad hoc 模型：

• 实践上比较方便
• 理论上不能严格证明：不能用于预测目的

Sharpe给出了一个非常相似的经济学模型：资本资产定价模型 Capital Asset Pricing Model CAPM

• 线性模型，因子是市场收益
• 从均值-方差分析推导
• 是均衡模型，可以用于预测资产价格
• 适用于所有资产和组合
• 用于期望值语境（收益都是指收益的期望值）

$$E[r_I-R]={\beta }_{I}E[r_M-R]$$

$$E[r_I]=R+{\beta }_{I}E[r_M-R]$$

CAPM模型表达的含义是，投资的风险回报：

• 与市场的风险回报成比例
• 比例常数为该投资的系统风险度量

平均而言，市场对我们承担的系统风险进行补偿

由于期望值算子和均衡参数，CAPM可以作为预测模型

在期望值语境下，资产自身的风险（残差项）不存在
从另外一个角度看，CAPM表示只有承担系统性风险会得到收益，承担个体风险没有回报（因为个体风险可以通过分散化完全消除）

多因子模型

CAPM模型推广到多因子模型：
$$r_i=R_F+\sum _{j=1}m{F}_j{\beta }_j^i+{ϵ}_i$$

• $r_i$ 资产$i$的实际收益
• $F_j$ 因子$j$的超额收益 $j=1,\cdots ,m$
• ${\beta }_j^i$ 资产$i$对因子$j$的敏感度
• $R_F$ 无风险利率
• ${ϵ}_i$ 反映资产$i$自身的风险(idiosyncratic risk)，是与市场风险无关的风险残差项（有关的部分已经用市场风险解释了）。假设${ϵ}_i\sim N(0,e_i^2)$，并且$Cov({ϵ}_i,{ϵ}_j)=0fori\ne j$

多因子模型：

• 是一个ad hoc模型
• 用于投资基金和对冲基金

均衡多因子模型

• 套利定价模型Arbitrage Pricing Theory (APT)
• The Fama-French model
• The Pastor and Stambaugh model

APT

$$E[r_j]=R_F+\sum _{j=1}^m{\lambda }_j{\beta }_j^i$$

• ${\lambda }_j$ 因子$j$的风险收益的期望值
• ${\beta }_j^i$ 资产$i$对因子$j$的敏感度
• $R_F$ 无风险利率

与CAPM模型对比

• 假设比CAPM少
• APT不要求所有投资者持有相同的市场组合
• 没有定义因子，实践中难以应用

与其他因子模型比较

• APT是均衡模型
• 截距项是无风险利率
• 因子是风险收益（不是surprises，也不是原始的金融数据）

Fama-French model

在CAPM模型的基础上增加两个因子：

• 小盘股-大盘股：market capitalization
• 价值股-成长股：Book-to-Market ratio

$$\begin{array}{rl}E[R_i-R_F]=& {\beta }_{mkt}E[R_{mkt}-R_F]\\ +& {\beta }_{SB}E[R_{small}-R_{big}]\\ +& {\beta }_{HL}E[R_{HBM}-R_{LBM}]\end{array}$$

• $R_{mkt}$ 价值加权的股指的收益
• $R_F$ 无风险利率
• $R_{small}$ 小盘股组合的收益
• $R_{big}$ 大盘股组合的收益
• $R_{HBM}$ 高Book-to-Market的股票（成长股）组合的收益
• $R_{LBM}$ 低Book-to-Market的股票（价值股）组合的收益
• ${\beta }_{mkt}$ 股票收益的敏感性，对价值加权股指
• ${\beta }_{SB}$ 股票收益的敏感性，对大小盘股收益差
• ${\beta }_{HL}$ 股票收益的敏感性，对价值股/成长股收益差

宽基股指：

• ${\beta }_{mkt}=1$
• ${\beta }_{SB}=0$
• ${\beta }_{HL}=0$

Carhart Model

$$\begin{array}{rl}E[R_i-R_F]=& {\beta }_{mkt}E[R_{mkt}-R_F]\\ +& {\beta }_{SB}E[R_{small}-R_{big}]\\ +& {\beta }_{HL}E[R_{HBM}-R_{LBM}]\\ +& {\beta }_{MOM}{L}_{MOM}\end{array}$$

• $L_{MOM}$ 动量风险收益
• ${\beta }_{MOM}$ 股票收益对流动性的敏感度

Pastor-Stambaugh Model

$$\begin{array}{rl}E[R_i-R_F]=& {\beta }_{mkt}E[R_{mkt}-R_F]\\ +& {\beta }_{SB}E[R_{small}-R_{big}]\\ +& {\beta }_{HL}E[R_{HBM}-R_{LBM}]\\ +& {\beta }_{L}LP\end{array}$$

• $LP$ 流动性风险收益
• ${\beta }_L$ 股票收益对流动性的敏感度

检验CAPM，APT和均衡模型

联合检验

• 模型的方程
• 模型的参数（股票的风险收益，因子个数等）

如果检验的结果是拒绝假设，应该归因于模型还是参数，或者同时归因于两者？

备选的优化规则

• 使用高阶矩（偏度、峰度）代替均值-方差
• 使用其他的风险度量方法
  • Shortfall probability
  • VaR
  • 条件VaR和Expected Shortfall
  • Worst case expectation
• 投资决策的行为面：behavioural portfolio theory 和 behavioural asset pricing model

Shortfall probability和Roy’s safety-first criterion

probability of shortfall ：组合收益率$R_P$低于阈值$R_L$的概率

Roy’s safety-first criterion的目的：找到最优的资产组合，使得组合的probability of shortfall最小。也就是求解如下优化问题：
$$\underset{{\omega }_1,\cdots ,{\omega }_n}{\min }P(R_P<R_L)$$

等价于
$$\underset{{\omega }_1,\cdots ,{\omega }_n}{\max }SFR({\omega }_1,\cdots ,{\omega }_n)=\frac{E[R_P]-R_L}{{\sigma }_P}$$

SFR是safety-first ratio的缩写，优化问题的目标是找到组合权重${\omega }_1,\cdots ,{\omega }_n$，使得SFR最大

Shortfall probability 和心理账户

Shortfall probability和Roy’s safety-first criterion与行为金融学修正后的资产组合理论高度相关

行为金融学视角下的资产组合管理认为个体：

• 不构建马科维茨投资组合，而是有几个相互独立的目的不同的“账户”（也就是子投资组合）。这个行为偏差称为心理账户mental accounting
• 用shortfall probability评估这些心理账户的业绩

2010年，马科维茨证明心理账户等价于均值-方差分析

风险调整后的业绩度量

Efficiency ratios

$$Efficiencyratios=\frac{Retuan}{Risk}$$

• Efficiency ratios是表达风险调整后的业绩的一般方法
• risk和return的定义可以多种多样

夏普比率vs特雷诺比率

两个指标都基于超额收益

夏普比率
$$SR=\frac{E[r_I]-R}{{\sigma }_I}$$

特雷诺比率
$$TR=\frac{E[r_I]-R}{{\beta }_I}$$

Jensen’s Alpha

度量风险调整后的超额收益

$$\alpha =r_I^{Actual}-R_I^{CAPM}=r_I^{Actual}-R-{\beta }_{I}E[r_M-R]$$

• $\alpha$ 主动收益：管理者的个人能力（买卖正确的资产）获得的收益
• $R+{\beta }_{I}E[r_M-R]$ 被动收益：暴露于系统风险获得的收益

Alpha Hunters and Beta Grazers

• Beta Grazers：被动管理基金($\alpha =0$)，只暴露在系统风险下（通常$\beta =1$）
• Alpha Hunters：不堵市场方向($\beta =0$)，只追求正的alpha收益

信息率

衡量主动基金经理的管理能力

用alpha的标准差衡量主动风险
$${\omega }_I={\sigma }_{{\alpha }_I}=SD[{\alpha }_I]$$

信息率
$$IR=\frac{\overline{{\alpha }_I}}{{\omega }_I}$$

MPT in Practice

在业界，MPT被当做一个参考框架：

• 理解资产组合的构建
• 估计金融风险
• 在公司金融中，用于估算股价

经典的MPT理论有两个主要缺点：

• 维度问题
• 参数估计

维度问题

由于金融市场的体量巨大，维度在过去和现在都是一个重要关注点。因子模型降低了维度的影响，但是没有解决所有问题：

• 非线性资产（债券、嵌入期权的资产）
• 应该如何使用指数/因子
• 随着时间推移，参数是否稳定

参数估计

• 细微的数据变化也会导致优化结果大不相同，这种现象称为“垃圾进垃圾出”
• 收益的方差和协方差即使经过很长时间，仍然非常稳定
• 需要数百年的金融数据对收益的期望值进行精确的估计
  • 几乎没有资产交易过足够长的时间
  • 市场条件发生变化，导致收益的时间序列发生中断(breaks)

解决思路

• 保持1-period框架并升级优化过程
  • 升级参数估计技术 (例如： 贝叶斯技术, Black-Litterman),
  • 使用更加鲁棒的优化技术 (例如：robust optimization, model averaging).
• 设计multi-period multi-scenario随机规划模型（stochastic programming models）。这种方法的优点：
  • 金融市场天然是动态的
  • 对收益分布的左尾进行更精确的建模，有助于在经济下行的时候避免金融危机