信号完整性分析6——电感的物理基础

信号完整性分析6——电感的物理基础

在两条信号线间的耦合，电源分布系统以及EMI 中，电感在信号沿均匀传输线传播的过程中产生突变，从而造成信号完整性问题。很多场合都要设法减小电感，例如减小信号路径间的互感以减小开关噪声，减小电源分布系统的回路电感和减小返回平面的有效电感以减小EMI，而有些场合则要优化电感，如获取所需的特征阻抗时。

6.1 电感的含义

电感是对表面磁场强度的数值积分

6.2 电感定律之一：电流周围将形成闭合磁力线围

磁力线圈是一个新的基本实体，它环绕在所有电流的周围。

• 如果把导体中的电流增大一倍，则电流周围磁力线圈的韦伯数也会增大一倍

• 导线的长度也会影响磁力线的匝数。导线越长，磁力线匝数就越多

• 导线的横截面，这是个二阶效应，并且更是难以捉模， 后面会知道， 如果增大横截面，如将导线做得粗一点，则磁力线匝数就会略有减少

• 附近的其他电流的存在也会对第一个电流周围的磁力线匝数产生影响。以返回电流为例，返回电流靠得越近，它的一些磁力线圈就越会环绕在第一个电流的周围．从而改变磁力线圈的总匝数。另一方面，电介质不会对电流周围的磁力线匝数产生影响。

  磁场根本不会与介质材料相互影响。即使电流被特氟纶(Teflon)或钛酸钡所包国，其周围的磁力线匝数也是不变的

• 只有当导体中含有铁、镍或钴时，构成导线的金属才会影响磁力线的总匝数这3 种金属称为铁磁金属，这些金属和含有这些金属的合金的导磁率都大于1。如果有磁力线圈完全包含在这些金属中，则这些金胧能使磁力线的匝数显著增加，但只是环绕在导体内部的磁力线圈受到影响。

6.3 电感定律之二：电感是导体上流过单位安培电流时，导体周图磁力线圈的韦伯值

电感主要与流过单位安培电流时导体周面的磁力线匝数有关。

电感是关于电流周围磁力线匝数的度量，而不是某一点磁场的绝对值。我们所关心 的不是磁场强度，而是磁力线的匝数。

用来度量电感的单位是1A 电流周围的磁力线圈的韦伯值。$1Wb/A$（韦伯、安培）称做$H$（亨利）。由于大多数互连线结构的电感都远小于1H, 所以通常以纳亨为单位，记为$nH$, 它是对导体通过单位安培电流时其周围的磁力线圈韦伯数大小的度量。
$$L=\frac{N}{I}$$
其中：
$L$ 表示电感，单位为$H$
$N$ 表示导体周围的磁力线匝数，单位为$Wb$
$I$ 表示导体中的电流，单位为$A$

若通过导体的电流加倍，磁力线的匝数也会加倍，但二者比率不变，且该比率与通过导体的电流完全无关。同样，磁力线的匝数改变时，表示这一比率的电感依然不变。

这说明电感实际上和导体的几何结构有关。影响电感的唯一因素就是导体的分布和在铁磁金属情况时导体的导磁率．

仅仅采用电感这一术语时，含义是十分模糊的。所以，要养成使用限定词的良好习惯，明确指出所指电感的准确类型。造成概念困惑最常见的根源就是混淆了电感的不同类型。

6.4 自感和互感

有两条临近的导线a 和b, 如果只有a 中有电流，其周围就会有磁力线圈和电感。如果在第二根导线b 中也有电流，则其周围也会有磁力线圈，从而也有一些电感。导线b产生的一些磁力线圈也将环绕住第一根导线a, 因此对于a 而言，环绕在它周围的磁力线圈一部分由其自身的电流产生，一部分由临近的第二根导线b 的电流产生。

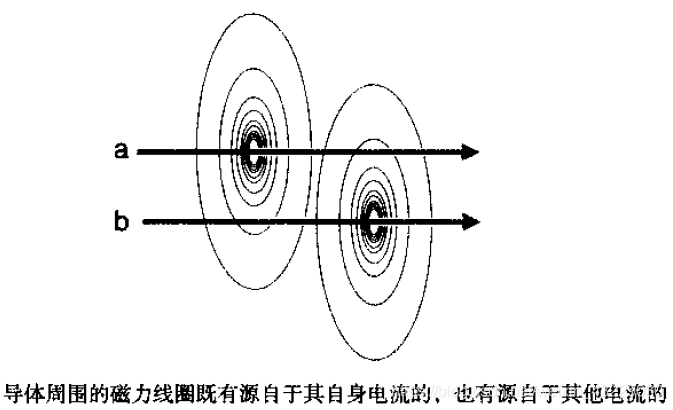
把一根导线自身电流产生的磁力线圈称为自磁力线圈(self-field line loop), 把由临近电流产生的磁力线圈称为互磁力线圈(mutual-field line loop) 。

• 任何源自b 而且环绕在a 周围的磁力线圈一定同时环绕着a 和b。于是我们说，互磁力线 “连接”着a 和b 两个导体。

• 用自感来指在导线中流过单位安培电流时所产生的环绕在导线自身周围的磁力线匝数。通常我们所说的电感实际上是导线的自感。

  导线的自感与其他导线的电流是无关的。如果把另一根通有电流的导线靠近第一根导线，则第一根导线周围的磁力线总匝数也会发生变化，但其自身电流所产生的磁力线匝数是不变的。

• 用互感来指一根导线中流过单位安培电流时产生的环绕在另一根导线周围的磁力线匝数。

  把两根导线拉近时，它们的互感会增大，反之则会减小。互感是磁力线圈匝数与电流的比率，所以仍用单位纳亨来度量互感。

  互感有两个不同寻常的微妙特性：

  1. 对称性

     无论是在第一根导线中加单位安培电流来测量第二根导线周围的磁力线圈匝数，还是在第二根中加单位安培电流来测量第一
     根导线周围的磁力线圈匝数，其得到的结果都是相同的。互感与涉及两根导线的磁力线圈有关，并且它与这两根导线的关系是同等的，即这个特性是两根导线同等共有的，所以有时把互感称为“两导线间的互感”。

     不管每根导线的形状和大小怎样，上述这个结论都是正确的。两根导线的几何形状可以不同

  2. 任意两导体间的互感都小于二者中任意一个的自感

6.5 电感定律之三：当导体周围的磁力线圈匝数变化时，导体两端将产生感应电压

磁力线圈有一个特殊性质：不管什么原因，只要一段导线周围的磁力线总匝数发生变化，导线两端就会产生电压。该电压与磁力线总匝数变化的快慢有着直接关系：
$$V=\frac{\Delta N}{\Delta t}$$
其中：
$V$ 表示导线两端的感应电压
$\Delta N$ 表示磁力线匝数的变化量
$\Delta t$ 表示磁力线匝数变化的时间

如果导线中的电流发生变化，则其周围的自磁力线圈的匝数也将变化，从而在导线两端产生电压。导线周围的磁力线匝数为$N=L\times I$, 其中 $L$ 是这段导线的自感。于是，导线两端所产生的电压（即感应电压）与导线的电感和导线中电流变化的快慢有关：
$$V=\frac{\Delta N}{\Delta t}=\frac{\Delta LI}{\Delta t}=L\frac{dI}{dt}$$

这个由电流变化产生的感应电压引起传输线效应、突变、串扰、开关噪声、轨道塌陷、地弹和大多数电磁于扰源(EMI)。

---

• 如上图，互磁力线匝数的变化在第一根导线的两端产生了感应电压。通常另一根导线中的电流发生变化时，我们用串扰来描述在临近导线上产生的感应电压噪声。在这种情况下，产生的电压噪声为：
  $$V_{noise}=M\frac{dI}{dt}$$
  其中：
  $V_{noise}$ 表示第一根导线中的感应电压噪声
  $M$ 表示两根导线之间的万感
  $I$ 表示第二根导线中的电流

  感应电压取决于电流变化的速度，所以有时候用开关噪声或 $\Delta I$ 噪声来描述电感线圈中电流切换时产生的噪声

6.6 局部电感

定义： 在计算磁力线圈的时候，假设这段导线所属的电流回路的剩余部分中不存在电流。由于仅考虑了电流回路的一部分，而且假设回路的其他部分不存在电流，所以把这种电感称为局部电感。一定要记住，当谈到局部电感时，回路的其他部分是不存在的。

分类：

1. 局部自感
2. 局部互感

对于直环形导线，值用简单的近似所计算的局部自感，其精度优于几个百分点，近似式如下：
L = 5 d { l n ( 2 d r ) − 3 4 } L=5d\{ln({\frac {2d}r})-{\frac 34}\} L=5d{ ln(r2d​)−43​}
其中：
$L$ 表示导线的局部自感，单位为 $nH$
$r$ 表示导线的半径，单位为 $in$
$d$ 表示导线的长度，单位为 $in$

导线的局部自感大约是$25nH/in$ 或$1nH/mm$（这仅是个经验法则，它虽易于使用，但是以牺牲精度为代价的）

• 局部自感的一个重要特性：电流分布越分散，局部电感就越小。反之， 电流分布密度越大，局部电感就越大。

两根直的圆导线的局部互感可以近似为：
M = 5 d { l n ( 2 d s ) − 1 + s d − ( s 2 d ) 2 } M=5d\{ln({\frac {2d}s})-1+{\frac sd}-({\frac s{2d}})^2\} M=5d{ ln(s2d​)−1+ds​−(2ds​)2}
其中：
$M$ 表示导线间的局部互感，单位为 $nH$
d d d<