基于软约束的轨迹（路径）优化原理公式推导详解

0 回顾

回顾$Minimum$ $Snap$当中的闭式求解的问题，闭式求解可以把轨迹变的更加顺滑，但是由于没有过多考虑障碍物的信息，可能会与障碍物发生碰撞。所以现在软约束的轨迹优化原理就是在原本顺滑性的基础上考虑代价碰撞函数，以及速度和加速度的限制。

---

---

1 软约束的轨迹优化

1.1 方法描述

优化方程：$\min {\lambda }_1{f}_s+{\lambda }_2{f}_o+{\lambda }_3\left(f_v+f_a\right)$，前面的这个顺滑性$f_s$就是之前在$Minimum$ $Snap$当中介绍过的表达式，又加入了$f_o$碰撞目标函数，以及$f_v$和$f_a$速度和加速度的目标函数，${\lambda }_1、{\lambda }_2、{\lambda }_3$是他们的权重系数。求解目标函数的最小值，可以采用梯度下降法。
轨迹依然是分成与$Minimum$ $Snap$当中的多段轨迹。
$p_{\mu }(t)=\{\begin{array}{lc}{\sum }_{j=0}^N{\eta }_{1j}{\left(t-T_0\right)}^j& T_0\le t\le T_1\\ {\sum }_{j=0}^N{\eta }_{2j}{\left(t-T_1\right)}^j& T_1\le t\le T_2\\ ⋮& ⋮\\ {\sum }_{j=0}^N{\eta }_{Mj}{\left(t-T_{M-1}\right)}^j& T_{M-1}\le t\le T_M\end{array}$

1.2 顺滑性目标函数的构建及其梯度

软约束轨迹优化方法是用来“完善”$Minimum$ $Snap$方法的，也用到了$Minimum$ $Snap$当中的一些理论，有关$Minimum$ $Snap$的推导可以去看之前的博客。首先就是把参数的映射成每段轨迹两个端点的$PVA$（位置，速度，加速度），$$\eta ={\mathbf{M}}^{-1}\mathbf{C}\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]$$
这样做的目的就是，让系数突出其物理含义。其中，$d_F$表示端点需要固定的一些值，$d_P$表示需要优化的一些值。$M^{-1}$表示在$Minimum$ $Snap$当中的$A^{-1}M$。$C$是类似的。将上面的$\eta$带入$Minimum$ $Snap$的顺滑性目标函数，即可得到以下表达式。
顺滑性的目标函数：
$$f_s={\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]}^T{\mathbf{C}}^T{\mathbf{M}}^{-T}\mathbf{Q}{\mathbf{M}}^{-1}\mathbf{C}\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]$$
把${\mathbf{C}}^T{\mathbf{M}}^{-T}\mathbf{Q}{\mathbf{M}}^{-1}\mathbf{C}$记作$R$矩阵，如下。
$$f_s={\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]}^T\left[\begin{array}{ll}{\mathbf{R}}_{FF}& {\mathbf{R}}_{FP}\\ {\mathbf{R}}_{PF}& {\mathbf{R}}_{PP}\end{array}\right]\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]$$
$R$阵通过$d_F、d_P$的下标被分为四块，分界的地方分为四块。之后对上述表达式进行求导处理，对$d_{p_{\eta }}$进行求导，$\eta$表示的是维度，因为在$x、y、z$三个方向都是用分段的多项式进行表示的，所以三个方向就得考虑$d_{p_x}、d_{p_y}、d_{p_z}$，就可以得出一个通式，如下方最后一行的式子，主要是为了简化符号，表示对一个轴的计算：
$$\begin{array}{rl}& {\mathbf{J}}_s=\left[\frac{\partial f_s}{\partial {\mathbf{d}}_{P_x}},\frac{\partial f_s}{\partial {\mathbf{d}}_{P_y}},\frac{\partial f_s}{\partial {\mathbf{d}}_{P_z}}\right],{\mathbf{H}}_s=\left[\frac{{\partial }^2{f}_s}{\partial {\mathbf{d}}_{P_x}^2},\frac{{\partial }^2{f}_s}{\partial {\mathbf{d}}_{P_y}^2},\frac{{\partial }^2{f}_s}{\partial {\mathbf{d}}_{P_z}^2}\right],\\ & \frac{\partial f_s}{\partial {\mathbf{d}}_{P_{\mu }}}=2{\mathbf{d}}_F^T{\mathbf{R}}_{FP}+2{\mathbf{d}}_P^T{\mathbf{R}}_{PP},\frac{{\partial }^2{f}_s}{\partial {\mathbf{d}}_{P\mu }^2}=2{\mathbf{R}}_{PP}^T,\end{array}$$
这就是一个对矩阵的求导，想象成数的求导就行。
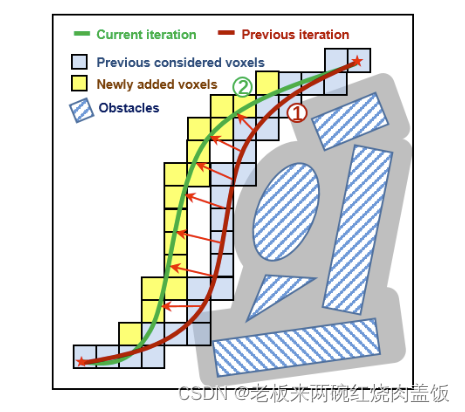
得到导数后，因为是凸函数，可以得到最优解，因为此时又考虑了碰撞的代价函数以及速度和加速度的代价函数，所以现在考虑顺滑性的代价函数所得到的最优解并不一定是全局的最优解。所以接下来考虑碰撞的目标函数。

1.3 碰撞目标函数的构建及其梯度

因为接下来的速度与加速度目标函数的构建与碰撞的目标函数构建方法大同小异，所以只列举碰撞目标函数的构建方法。

1. 引入$Penalty$ $Function$，当$UAV$距离障碍物很近的时候，将这个函数值设置的非常大，使得$UAV$远离这个障碍物；但是当$UAV$出于一个非常安全的情况下，就把这个函数值设置的小一点，以便快速通过空旷区域。
2. 惩罚函数是可微的，可以选择如下式子所示的指数函数：$$c(d)=\alpha \cdot \exp \left(-\left(d-d_0\right)/r\right)$$$d_0$表示的是一个安全距离，$d$表示的是无人机当前在一个位置（与障碍物之间的距离），假如这个$d$非常接近障碍物了，所以此时的$d$肯定是要小于安全距离$d_0$的，所以$d-d_0$就是一个负数，则$-(d-d_0)$就是一个正数，而$r$是个系数可以自定的，假设$r=0.1$，此时的这个指数$exp$的数值就会很大，所以整个惩罚函数的值就会非常大，这样就使得无人机会远离障碍物，其实基于软约束的这种方法和人工势场法的思想会不会有点类似？
3. 轨迹是一条曲线，轨迹上的点都必须去计算这个惩罚函数。每个点都考虑的话就差不多是个线积分，就沿着轨迹$d_s$进行积分，积分其实就是个累加的想法，把每个点加起来，因为是$d_s$积分，所以可以用每一小段的速度乘以时间$d_t$进行代替$d_s$，这个速度$v(t)$要注意一下，这是$x、y、z$三个方向的速度合并后的一个速度，也就是无人机真实的速度。$$\begin{array}{rl}{f}_o& ={\int }_{T_0}^{T_M}c(p(t))ds\\ & ={\int }_{T_0}^{T_M}c(p(t))\Vert v(t)\Vert dt=\sum _{k=0}^{\tau /\delta t}c\left(p\left({\mathcal{T}}_k\right)\right)\Vert v(t)\Vert \delta t\end{array}$$
   其中$\Vert v(t)\Vert =\sqrt{(v_x{)}^2+(v_y{)}^2+(v_z{)}^2}$。
   上述式子因为没有一个理论的表达式，所以进行离散化处理。
4. 求导，过程类似顺滑性约束的目标函数求导，对三个方向分别求导，通式为对$d_{p_{\mu }}$求导的式子，因为三个轴的求法都是一样的。
   $$\begin{array}{rl}& {\mathbf{J}}_o=\left[\frac{\partial f_o}{\partial {\mathbf{d}}_{P_x}},\frac{\partial f_o}{\partial {\mathbf{d}}_{P_y}},\frac{\partial f_o}{\partial {\mathbf{d}}_{P_z}}\right]\\ & \frac{\partial f_o}{\partial {\mathbf{d}}_{P_{\mu }}}=\sum _{k=0}^{\tau /\delta t}\left\{{\nabla }_{\mu }c\left(p\left({\mathcal{T}}_k\right)\right)\Vert v\Vert \mathbf{F}+c\left(p\left({\mathcal{T}}_k\right)\right)\frac{v_{\mu }}{\Vert v\Vert }\mathbf{G}\right\}\delta t,(9)\end{array}$$
   对$c\left(p\left({\mathcal{T}}_k\right)\right)\Vert v(t)\Vert \delta t$这部分进行求导，可以使用乘法求导的法则，即$c\left(p\left({\mathcal{T}}_k\right)\right)$的导数乘以$\Vert v(t)\Vert$再加上$c\left(p\left({\mathcal{T}}_k\right)\right)$乘以$\Vert v(t)\Vert$的导数。上方求导后的$\mathbf{F}$就是对第一项求导后所产生的项，$\mathbf{G}$就是对第二项求导后产生的项。$\left(p\left({\mathcal{T}}_k\right)\right)$就是$\eta \ast \mathbf{T}$得来的。$\eta ={\mathbf{M}}^{-1}\mathbf{C}\left[\begin{array}{l}{\mathbf{d}}_F\\ {\mathbf{d}}_P\end{array}\right]$，现在引进一个新的符号$L_{dp}$来指代$\eta$当中对$d_p$求导后的项，所以可以得到$\mathbf{F}=\mathbf{T}{\mathbf{L}}_{dp}$，$\mathbf{G}=\mathbf{T}{\mathbf{V}}_m{\mathbf{L}}_{dp}$。然后对速度求导的时候，因为有根号，所以套用有根号的函数求导公式。${\nabla }_{\mu }$就是碰撞代价在某个轴（$x、y、z$）上的梯度。
5. 软约束优化中还得到了$Hessian$矩阵（一阶导数再求导），了解即可如下：$$\begin{array}{rl}& {\mathbf{H}}_o=\left[\frac{{\partial }^2{f}_o}{\partial {\mathbf{d}}_{P_x}^2},\frac{{\partial }^2{f}_o}{\partial {\mathbf{d}}_{P_y}^2},\frac{{\partial }^2{f}_o}{\partial {\mathbf{d}}_{P_z}^2}\right]\\ & \frac{{\partial }^2{f}_o}{\partial {\mathbf{d}}_{P\mu }^2}=\sum _{k=0}^{\tau /\delta t}\{{\mathbf{F}}^T{\nabla }_{\mu }c(p\left({\mathcal{T}}_k\right)\frac{v_{\mu }}{\Vert v\Vert }\mathbf{G}+{\mathbf{F}}^T{\nabla }_{\mu }^{2}c\left(p\left({\mathcal{T}}_k\right)\right)\Vert v\Vert \mathbf{F}\\ & +{\mathbf{G}}^T{\nabla }_{\mu }c\left(p\left({\mathcal{T}}_k\right)\right)\frac{v_{\mu }}{\Vert v\Vert }\mathbf{F}+{\mathbf{G}}^{T}c\left(p\left({\mathcal{T}}_k\right)\right)\frac{v_{\mu }^2}{\Vert v{\Vert }^3}\mathbf{G}\}\delta t\end{array}$$
6. 其他的速度约束与加速度约束差不多构建，就不细说了。
7. 这样就有了三部分的雅克比矩阵了，$\mathbf{J}={\lambda }_1{\mathbf{J}}_s+{\lambda }_2{\mathbf{J}}_o+{\lambda }_3\left({\mathbf{J}}_v+{\mathbf{J}}_a\right)$ ， $\mathbf{H}={\lambda }_1{\mathbf{H}}_s+{\lambda }_2{\mathbf{H}}_o+{\lambda }_3\left({\mathbf{H}}_v+{\mathbf{H}}_a\right)$，以上就是碰撞速度加速度目标函数及其梯度的构建步骤。

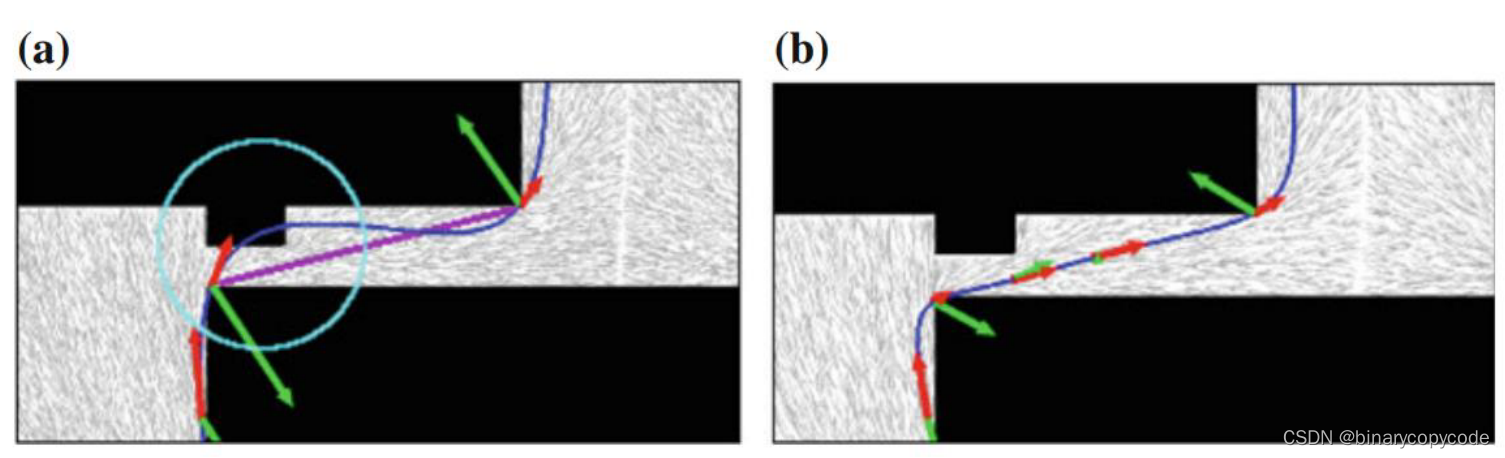
2 软约束轨迹优化方法的优缺点

地图上保留了当前点和距离最近的障碍物及其导数，安全距离$d$和$d_0$之类的信息，看图说明也是和人工势场法比较相似。

如果比较近（与障碍物），就会有力把无人机往外推，防止碰撞；如果比较远，力就不会那么大。

这个方法也有一些确定，从名字上就可以体现出来，因为是软约束的方法，有好几个优化目标，可能会导致函数取到局部最优解，当地形比较复杂的时候，可能会陷入局部最优解反而出不来，但是大多数情况下还是能找到最优解的。

3 Code

Code下次来仿真。