第二章(第3讲)三维空间刚体运动
2.1 旋转矩阵
2.1.1 点和向量,坐标系
如果我们确定一个坐标系,也就是一个线性空间的基 ,那就可以谈论向量 a 在这组基下的坐标了:
向量的内积可以描述向量间的投影关系。
向量的外积可表示向量的旋转,原因:外积的方向(右手法则)为旋转向量的方向,外积的大小
由向量转过的角度决定。
2.1.2 坐标系间的欧氏变换
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。

旋转变换:描述相机的旋转
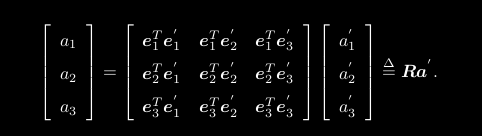
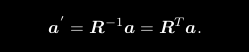
矩阵 R 描述了旋转本身。因此它又称为旋转矩阵。旋转矩阵有一些特别的性质。事实上,它是一个行列式为 1 的正交矩阵,反之,行列式为 1 的正交矩阵也是一个旋转矩阵。旋转矩阵的集合定义
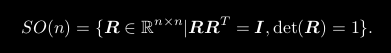
欧式变换=旋转+平移,故需加入平移向量,所以完整的欧式变换表达式为
![]()
2.1.3 变换矩阵与齐次坐标
欧式变换关系不是线性关系,需引入齐次坐标和变换矩阵
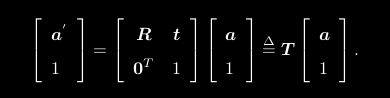
齐次坐标:三维向量末尾添1变为四维向量
矩阵T称为变换矩阵(Transform Matrix)
在齐次坐标中,某个点 x 的每个分量同乘一个非零常数 k 后,仍然表示的是同一个点。因此,一个点的具体坐标值不是唯一的。如 和
是同一个点。但当最后一项不为零时,我们总可以把所有坐标除以最后一项,强制最后一项为 1,从而得到一个点唯一的坐标表示(也就是转换成非齐次坐标),这时,忽略掉最后一项,这个点的坐标和欧氏空间就是一样的。依靠齐次坐标和变换矩阵,两次变换的累加就可以有很好的形式。在不引起歧义的情况下,以后我们就直接把它写成
的样子,默认其中是齐次坐标了。
变换矩阵T这种矩阵又称为特殊欧氏群(Special Euclidean Group):
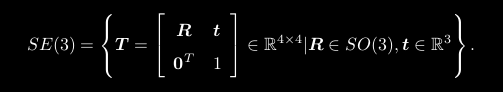
同样T矩阵的逆表示一个反向的变换:
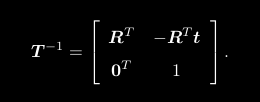
旋转矩阵R与变换矩阵T的缺点
- 旋转矩阵R矩阵用9个量描述一次旋转只有三个自由度的变换,变换矩阵T用16个量描述六个自由度的变换,表达冗余。
- 旋转矩阵R必须为正交矩阵且行列式为1,当我们想要估计或优化一个旋转矩阵/变换矩阵时,这些约束会使得求解变得更困难。
2.2 旋转向量和欧拉角
2.2.1 旋转向量
任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(李代数)(或轴角, Axis-Angle)。这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
假设有一个旋转轴为 n,角度为 θ 的旋转,显然,它对应的旋转向量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式(Rodrigues's Formula)表明:
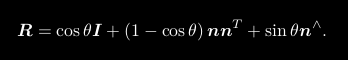
符号∧是向量到反对称的转换符,具体转换过程如下图所示:
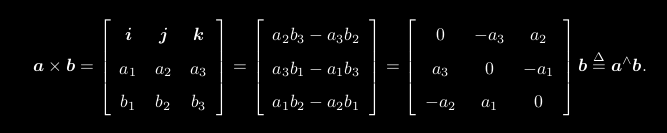
对于转角θ:
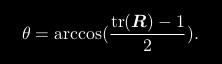
对于转轴n,由于旋转轴上的向量在旋转后不发生改变,有
![]()
2.2.2 欧拉角
欧拉角提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。欧拉角当中比较常用的一种,便是用“偏航-俯仰-滚转”(yaw-pitch-roll)三个角度来描述一个旋转的,等价于 ZYX 轴的旋转。
- 绕物体的 Z 轴旋转,得到偏航角 yaw;
- 绕旋转之后的 Y 轴旋转,得到俯仰角 pitch;
- 绕旋转之后的 X 轴旋转,得到滚转角 roll。
此时,我们可以使用这样一个三维的向量描述任意旋转。
欧拉角优点:直观,常用于人机交互
欧拉角缺点:万向锁问题(Gimbal Lock):在俯仰角为±90°时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次旋转变成了两次旋转)。
2.3 四元数
2.3.1 四元数定义
事实上,我们找不到不带奇异性的三维向量描述方式,四元数(Quaternion)是 Hamilton 找到的一种扩展的复数. 它既是紧凑的,也没有奇异性。如果说缺点的话,四元数不够直观,其运算稍为复杂一些。一个四元数 q 拥有一个实部和三个虚部。

在四元数中,任意的旋转都可以由两个互为相反数的四元数表示。
2.3.2 四元数运算
加减
![]()
乘法
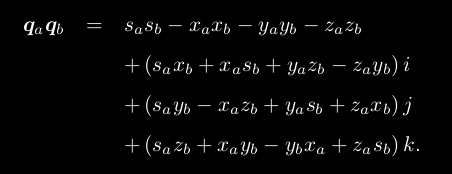
![]()
由于最后一项外积的存在,四元数乘法通常是不可交换的,除非 v a 和 v b 在 R 3中共线,那么外积项为零。
共轭
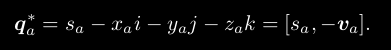
![]()
模长
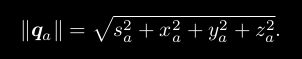
![]()
逆

数乘与点乘
![]()
![]()
2.3.3 用四元数表示旋转

2.3.4 四元数与旋转矩阵的转换























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








