CAUSALTIME: REALISTICALLY GENERATED TIME- SERIES FOR BENCHMARKING OF CAUSAL DISCOVERY

系列文章目录

Causaltime：实际生成的时间序列，用于因果发现的基准测试 ICLR2024

---

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

---

摘要

时间序列因果发现（TSCD）是机器学习的一个基本问题。 然而，现有的合成数据集无法正确评估或预测算法在真实数据上的性能。 本研究引入了 CausalTime 管道来生成与真实数据高度相似的时间序列，并使用真实因果图进行定量性能评估。 该管道从特定场景中的真实观察开始，并生成匹配的基准数据集。 首先，我们利用深度神经网络和标准化流程来准确捕捉现实动态。 其次，我们通过对神经网络进行重要性分析或利用先验知识来提取假设的因果图。 第三，我们通过将因果模型分为因果项、残差项和噪声项来导出真实因果图。 最后，使用拟合网络和导出的因果图，我们生成适合算法评估的相应通用时间序列。 在实验中，我们通过定性和定量实验验证生成数据的保真度，然后使用这些生成的数据集对现有 TSCD 算法进行基准测试。 CausalTime为在实际应用中评估TSCD算法提供了可行的解决方案，并且可以推广到广泛的领域。 为了方便使用所提出的方法，我们还提供了一个用户友好的网站，托管在 www.causaltime.cc 上。

---

提示：以下是本篇文章正文内容

一、引言

从时间序列推断因果结构，即时间序列因果发现（TSCD），是机器学习中的一个基本问题。 它超越了预测或预测，揭示了多变量时间序列下隐藏的复杂相互作用。 最近，人们提出了许多算法（Lìowe et al., 2022; Li et al., 2020; Wu et al., 2022; Brouwer et al., 2021）并取得了令人满意的性能，即发现的因果图是 接近地面真实对应物。 在某些设置下，因果发现结果近乎完美，AUROC 分数接近 1。

然而，TSCD 算法的基准不足以进行性能评估。 首先，为了定量评价结果的统计显着性，数据集在质量和数量上都需要提高。 其次，当前的数据集仅限于几个领域，没有涵盖广泛的应用方向。 更重要的是，具有真实因果图的数据集是合成的，可能会偏离真实的数据生成过程，因此分数可能无法反映真实数据的性能（Reisach et al., 2021）。

尽管最近的工作还提出了更好的时间序列因果发现基准（Lawrence 等人，2021；Runge 等人，2020）以及静态设置（Góobler 等人，2023；Chevalley 等人） ., 2023a;b)，当前的 TSCD 算法通常包含三种类型的数据集：数值数据集，例如 VAR（向量自回归）和 Lorenz-96（Karimi & Paul，2010），使用闭式方程进行模拟。 尽管其中一些方程 (Lorenz-96) 受到实际应用场景的启发，例如气候动力学，但它们过于简化，并且对现实世界应用的通用性非常有限 (Runge et al., 2020)。 准真实数据集由手动设计的动态生成的时间序列组成，模拟特定场景下的真实数据集。 例如，DREAM3（Prill et al., 2010）是使用基因表达和调控动力学模拟的数据集，而NetSim（Smith et al., 2011）是通过模拟功能磁共振成像观察下人脑区域之间的相互作用而生成的。 此类数据集的问题在于，它仅涵盖了一些基础机制相对清楚的研究领域。 对于医疗保健或金融等领域，很难甚至不可能通过手动设计的动态生成真实的时间序列。 真实数据集（例如 MoCap (Tank et al., 2022)、S&P 100 股票收益 (Pamfil et al., 2020)）不存在上述问题，但问题在于地面真相因果图大多无法访问 ，我们必须诉诸一些临时解释。 如表所示。 1、目前可用的基准测试工具无法支持对时序因果发现算法的综合评估。 因此，非常需要一种生成基准的方法，该方法可以高度模仿不同场景中的真实数据并具有真实的因果图。
表 1：时间序列因果发现评估基准的比较。

在这项工作中，我们提出了一种新颖的管道，能够生成真实的时间序列和地面真实因果图，并且可以推广到不同的领域，称为 CausalTime。 生成具有给定因果图的时间序列的过程可以使用自回归模型来实现，但是，追求与目标时间序列高精度匹配的因果图并非易事，特别是对于对底层基础知识了解甚少的数据 因果机制。 为了解决这个问题，我们建议使用深度神经网络来高精度地拟合观察到的数据，然后从网络或具有高数据保真度的先验知识中检索因果图。 具体来说，我们首先通过对神经网络进行重要性分析或利用先验知识来获得假设的因果图，然后将函数因果模型分为因果项、残差项和噪声项。 分割模型可以自然地生成与原始数据观测很好匹配的时间序列。 值得注意的是，因果图的检索不是因果发现过程，并不一定能揭示潜在的因果关系，但可以产生现实的时间序列作为因果发现算法的基准。 我们的基准是开源且用户友好的，我们的网站位于 www.causaltime.cc。 具体来说，我们的贡献包括：

• 我们提出了CausalTime，一种通过真实因果图生成真实时间序列的管道，它可以应用于不同的领域，并为评估TSCD 算法提供新的选择。
• 我们进行定性和定量实验，以验证生成的时间序列保留了原始时间序列的特征。
• 我们在生成的数据集上评估了几种现有的TSCD 算法，为算法比较、选择和改进提供了一些指导。

二、 RELATED WORKS

因果发现。 因果发现（或因果结构学习），包括静态设置和动态时间序列，一直是机器学习的热门话题，并在过去几十年中取得了巨大进展。 这些方法可以粗略地分为多个类别。 (i) 基于约束的方法，例如 PC (Spirtes & Glymour, 1991)、FCI (Spirtes et al., 2000) 和 PCMCI (Runge et al., 2019b; Runge, 2020; Gerhardus & Runge, 2020)， 通过执行条件独立性测试来构建因果图。 (ii) 基于分数的学习算法，包括惩罚神经常微分方程和非循环约束（Bellot 等人，2022）（Pamfil 等人，2020）。 (iii) 基于加性噪声模型 (ANM) 的方法，该方法基于加性噪声假设推断因果图（Shimizu 等人，2006 年；Hoyer 等人，2008 年）。 Hoyer 等人扩展了 ANM。 (2008) 到具有几乎任何非线性的非线性模型。 (iv) 基于格兰杰因果关系的方法。 格兰杰因果关系最初由 Granger (1969) 提出，他提出通过测试一个时间序列对预测另一个时间序列的帮助来分析时间因果关系。 最近，深度神经网络（NN）已广泛应用于非线性格兰杰因果关系发现。 （Wu 等人，2022；Tank 等人，2022；Khanna 和 Tan，2020；Lowe 等人，2022；Cheng 等人，2023b）。 (v) Sugihara 等人提出的收敛交叉映射（CCM）。 (2012) 重建不可分离弱连接动态系统的非线性状态空间。 这种方法后来扩展到同步、混杂或零星时间序列的情况（Ye et al., 2015；Benk˝o et al., 2020；Brouwer et al., 2021）。 这个方向的丰富文献需要有效的定量评估，并且这个方向的进展也启发了设计新的基准测试方法。 在本文中，我们建议使用因果模型生成基准数据集。

因果发现的基准。 基准测试对于算法设计和应用至关重要。 研究人员提出了不同的数据集和评估指标，用于静态和时间序列设置下的因果发现。 (i) 静态设置。 数值、准真实和真实数据集都广泛用于静态因果发现。 数值数据集包括使用线性、多项式或三角函数模拟的数据集（Hoyer et al., 2008；Mooij et al., 2011；Spirtes & Glymour, 1991；Zheng et al., 2018）； 准真实数据集是根据物理定律（例如双摆（Brouwer et al., 2021））或现实场景（例如合成双胞胎出生数据集（Geffner et al., 2022）、用于患者监测的报警消息系统（Scutari, 2010）生成的 ；Lippe 等人，2021）、神经活动数据（Brouwer 等人，2021）和基因表达数据（Van den Bulcke 等人，2006）； 真实数据集的使用频率较低。 例子包括火山喷发的“Old Faithful”数据集（Hoyer et al., 2008），以及人类免疫系统细胞中蛋白质和磷脂的表达水平（Zheng et al., 2018）。 最近，Göobler 等人。 (2023) 提出了一种新颖的管道，即 causalAssembly，在制造场景中生成现实且复杂的装配线。 谢瓦利等人。 (2023a) 和 Chevalley 等人。 另一方面，(2023b) 提供了 CausalBench，这是一组来自大规模单细胞扰动的真实数据的基准。 尽管 causalAssembly 和 CausalBench 是经过精心设计的，但它们在某些研究领域受到限制，在这些领域中，动态可以很容易地复制，或者可以通过执行干预来获取真实的因果关系。 (ii) 时间序列设置。 在时间序列设置中，广泛使用的数值数据集包括 VAR 和 Lorenz-96 (Tank et al., 2022; Cheng et al., 2023b; Khanna & Tan, 2020; Bellot et al., 2022)； 准真实数据集包括 NetSim (Lìowe et al., 2022)、Dream-3 / Dream-4 (Tank et al., 2022) 和使用 Fama-French 三因子模型模拟的金融数据集 (Nauta et al., 2022)。 ，2019）； 真实数据集包括人体运动数据的 MoCap 数据集（Tank 等人，2022）、S&P 100 股票数据（Pamfil 等人，2020）、热带气候数据（Runge 等人，2019b）和复杂生态系统数据（Sugihara 等人） 等，2012）。 除了这些数据集之外，还有一些作品提供了带有真实因果图的新颖基准。 CauseMe（Runge et al., 2020; 2019a）为数值、准真实和真实数据集提供了一个平台1，这些数据集主要基于气候情景下的 TSCD 挑战。 然而，尽管该平台设计良好且用户友好，但它并没有减轻保真度、地面真实可用性和领域通用性之间的权衡。 例如，CauseMe 中的数值数据集仍然不现实，真实数据集的真实因果图仍然基于可能不正确的领域先验知识。 （Lawrence 等人，2021）专注于生成超越 CauseMe 的时间序列数据集。 他们的框架允许研究人员灵活地生成具有各种属性的大量数据。 他们生成的数据集的真实图是准确的，但 Lawrence 等人的函数依赖关系。 （2021）仍然是手动设计的，可能无法反映自然场景中的真实动态。 因此，他们生成的数据集仍然被分类为选项卡中的数值数据集。 1，虽然具有更高的灵活性。

最近，神经网络因其生成时间序列的能力而被广泛研究。 （2019）； 贾勒特等人。 （2021）； 裴等人。 （2021）； 康等人。 （2020）； 张等人。 （2018）； 埃斯特万等人。 （2017）。 然而，用这些方法生成的时间序列不适合对因果发现进行基准测试，因为因果图不是与序列一起生成的。 因此，我们提出了一个生成真实时间序列以及真实因果图的管道。

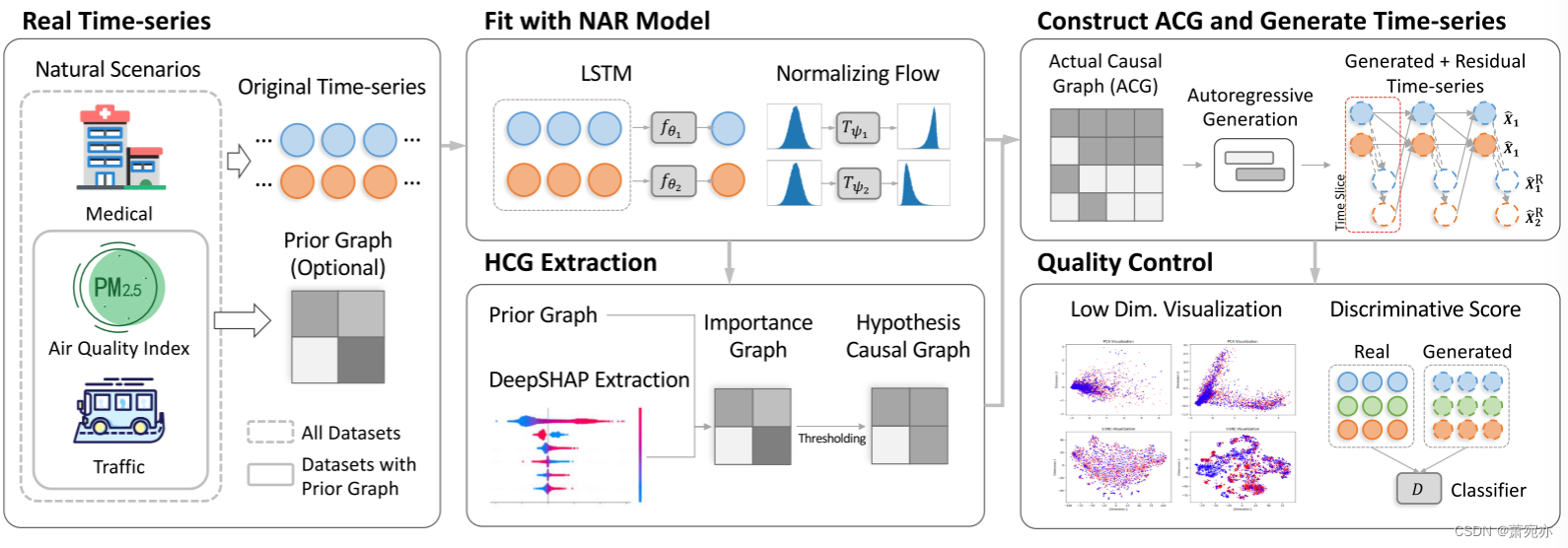
图 1：CausalTime 管道的图示。 我们将真实场景中的观察结果与 NAR 模型进行拟合，然后拆分模型并重新组织组件以构建实际因果图（ACG），该因果图可以生成与输入观察结果类似的时间序列。 经过视觉和定量质量控制后，合成的时间序列和相应的 ACG 作为评估 TSCD 算法在实际应用中性能的基准。

三、 拟议的时间序列生成流程

为了生成与真实场景中的观察结果高度相似的时间序列，并利用地面真相因果图，我们提出了一个通用框架来生成根据真实观察结果构建的因果图，并生成与这些观察结果高度相似的对应时间序列。 整个流程由几个关键步骤组成，如图 1 所示。虽然原始时间序列的真实因果图未知，但构建的因果图作为生成版本下的基本事实，它们一起充当 TSCD 算法的基准，如图 2 所示。我们想澄清的是，我们的生成管道基于因果发现文献中常见的几个假设：马尔可夫条件、忠实性、充分性、无瞬时效应和平稳性。 我们在补充材料中详细讨论了这些假设。 A.1.1 节由于页数限制。

3.1 CAUSAL MODEL

时间序列中的因果模型通常表示为图形模型（Vowels 等人，2021；Spirtes 等人，2000）。 然而，与经典的Pearl因果关系（Pearl，2009）不同，时间序列数据必须考虑时空结构依赖性。 我们将动态系统的均匀采样观测表示为 X = { x 1 : T , i } i = 1 N X=\{x_{1:T,i}\}_{i=1}^{N} X={x1:T,i​}i=1N​，其中 $x_t$ 是时间点 t 的样本向量，由 N 个变量 { x t , i } , \{x_{t,i}\}, {xt,i​},组成，其中 t ∈ { 1 , . . . , T } a n d i ∈ { 1 , . . . , N } t\in\{1,...,T\}\mathrm{and} i\in\{1,...,N\} t∈{1,...,T}andi∈{1,...,N}。 时间序列的结构因果模型 (SCM) (Runge et al., 2019b) 为 $x_{t,i}=f_i\left(\mathcal{P}(x_{t,i}),{\eta }_{t,i}\right)$, i = 1, 2, …,N, 其中 $f_i$是任何（可能）非线性函数，${\eta }_{t,i}$表示相互独立的动态噪声，$\mathcal{P}(x_t^j)$ 表示$x_t^j$的因果父代。 该模型可以推广到大多数场景，但可能会给我们的实现带来障碍。 在本文中，我们考虑非线性自回归模型 (NAR)，这是 SCM 的一个稍微受限的类别。

非线性自回归模型。 我们在许多时间序列因果发现算法中采用了这种表示（(Tank et al., 2022; Láowe et al., 2022; Cheng et al., 2023b)），以及 Lawrence et al.。 (2021) 的时间序列生成管道。 在非线性自回归模型 (NAR) 中，假设噪声是独立且可加的，每个采样变量 $x_{t,i}$由以下方程生成：

其中$\mathcal{P}(\cdot )$表示因果图中的父母。 我们进一步假设因果效应的最大时滞是有限的。 那么模型可以表示为 x t , i = f i ( { x τ , j } x τ , j ∈ P ( x t , i ) ) + η t , i . x_{t,i}=f_{i}\left(\{x_{\tau,j}\}_{x_{\tau,j}\in\mathcal{P}(x_{t,i})}\right)+\eta_{t,i}. xt,i​=fi​({xτ,j​}xτ,j​∈P(xt,i​)​)+ηt,i​.。 这里$t-\tau \le {\tau }_{\max },\forall x_{\tau ,j}\in \mathcal{P}(x_{t,i})$，${\tau }_{\max }$ 表示最大时滞。 在因果发现中，通常假设时间同质性（Gong et al., 2023），即函数 $f_i$ 和因果父项$\mathcal{P}$ 与时间无关。 通过汇总时间依赖性，因果模型的汇总图可以用二元矩阵 A 表示，其中其元素 $a_{ji}=\{\begin{array}{cc}1,& \exists \tau ,s.t.,x_{\tau ,j}\in \mathcal{P}(x_{t,i})\\ 0,& \mathrm{otherwise}\end{array}$，否则 。 用于因果发现的数据集对是⟨X,A⟩。 TSCD 的目标是恢复给定时间序列 X 的矩阵 A。然而，由于对于大多数实时时间序列 X，因果图 A 是未知的，因此用实时时间序列对因果发现算法进行基准测试通常是不合适的。

3.2 TIME-SERIES FITTING

在收集来自不同领域的实时序列后，我们用深度神经网络和归一化流来拟合多元时间序列的动态过程。
使用因果解缠神经网络 (CDNN) 进行时间序列拟合。 为了用深度神经网络拟合观察到的时间序列，并将随意图引入网络的输出序列预测中，Tank 等人。 （2022）； 卡纳和谭 (2020)； 程等人。 (2023b) 使用 N 个单独的 MLP / LSTM 将父母的因果效应分离到每个单独的输出系列，这被称为组件式 MLP / LSTM (cMLP / cLSTM)。 在本文中，我们遵循（Cheng et al., 2023a）的定义，并将组件式神经网络称为“因果解缠神经网络”（CDNN），即采用 fθ(X,A) 形式的神经网络 $\begin{array}{r}{\mathbf{f}}_{\Theta }(\mathbf{X},\mathbf{A})=[f_{{\Theta }_1}(\mathbf{X}\odot {\mathbf{a}}_{:,1}),...,f_{{\Theta }_n}(\mathbf{X}\odot {\mathbf{a}}_{:,n}){]}^T\end{array}$，其中 A ∈ { 0 , 1 } n × n \mathbf{A}\in\left\{0,1\right\}^{n\times n} A∈{0,1}n×n 且算子 ⊙ 定义为 f ϕ j ( X ⊙ a : , j ) = Δ f ϕ j ( { x 1 ⋅ a 1 j , . . . , x N ⋅ a N j } ) f_{\phi_{j}}(\mathbf{X}\odot\mathbf{a}_{:,j})\stackrel{\Delta}{=}f_{\phi_{j}}\left(\{\mathbf{x}_{1}\cdot a_{1j},...,\mathbf{x}_{N}\cdot a_{Nj}\}\right) fϕj​​(X⊙a:,j​)=Δfϕj​​({x1​⋅a1j​,...,xN​⋅aNj​})。
到目前为止，函数$f_{{\Theta }_j}(\cdot )$充当神经网络函数，用于逼近方程 1 中的 $f_j(\cdot )$。 (1). 由于我们没有先验地假设潜在的因果关系，为了高精度地提取时间序列的动态，我们将生成过程与所有历史变量进行拟合（最大时间滞后${\tau }_{\max }$，在补充部分 A.1.1 中讨论）和 获得全连接的预测模型。 具体来说，我们假设

下面，我们省略${\mathbf{x}}_{t-\tau :t-1,j}$的时间维度，用${\mathbf{x}}_j$表示。 使用 CDNN，我们可以用 $f_{{\Theta }_i}(\cdot )$近似$f_i(\cdot )$。 (Tank et al., 2022) 和 (Cheng et al., 2023b) 使用组件式 MLP / LSTM (cMLP / cLSTM) 实现 CDNN，但该结构高度冗余，因为它由 N 个不同的神经网络组成。

CDNN 的实施。 CDNN 的实现可能有所不同。 例如，程等人。 (2023a) 探索通过基于消息传递的神经网络增强因果发现，这是具有广泛权重共享的 CDNN 的特殊版本。 在这项工作中，我们利用带有共享解码器的基于 LSTM 的 CDNN（实现细节如附录 A.2 节所示）。 此外，我们执行计划采样（Bengio et al., 2015）以减轻执行自回归生成时的累积误差。

通过归一化流进行噪声分布拟合。 在用$f_{{\Theta }_i}(\cdot )$近似函数项 $f_i(\cdot )$后，我们用归一化流 (NF) 近似噪声项 ${\eta }_{t,i}$ （Kobyzev 等人，2021 年；Papamakarios 等人，2021 年）。 主要过程描述为 ${\hat{\eta }}_{t,i}$ =$T_{{\psi }_i}(u)$，其中$u\sim p_u(u)$，其中$T_{{\psi }_i}(\cdot )$ 是神经网络实现的可逆可微变换，$p_u(u)$是基分布（正态分布） 分布在我们的管道中），并且 $p_{{\hat{\eta }}_i}({\hat{\eta }}_{t,i})=p_u(T_{{\psi }_i}^{-1}({\hat{\eta }}_{t,i}))\frac{\partial }{\partial {\hat{\eta }}_{t,i}}{T}_{{\psi }_i}^{-1}({\hat{\eta }}_{t,i}).$。 那么，优化问题可以表述为 ${\max }_{{\psi }_i}{\sum }_{t=1}^N\log p_u(T_{{\psi }_i}^{-1}({\eta }_{t,i}))+\log \frac{\partial }{\partial {\eta }_{t,i}}{T}_{{\psi }_i}^{-1}({\eta }_{t,i})$。

3.3 EXTRACTION OF HYPOTHETICAL CAUSAL GRAPH 假设因果图的提取

在完全连接的预测模型中，所有 N 个变量都对每个预测都有贡献，这与观察结果非常吻合，但比潜在因果图过于复杂。 现在，我们通过识别预测模型$f_{{\Theta }_i}(\cdot )$中贡献最大的变量来提取假设因果图 (HCG) H。 我们想澄清的是，提取 HCG 并不是因果发现，而是旨在识别有贡献的因果父母，同时保持拟合模型的保真度。 我们的流程中包含两个选项： i) 使用 DeepSHAP 提取 HCG； ii) 利用先验知识提取 HCG。

使用 DeepSHAP 提取 HCG。 Shapley 值（Sundararajan & Najmi，2020）经常用于为回归模型分配特征重要性。 它起源于合作博弈论（Kuhn & Tucker，2016），最近被开发用于解释深度学习模型（DeepSHAP）（Lundberg & Lee，2017；Chen 等人，2022）。 对于每个预测模型$f_{{\Theta }_i}(\cdot )$，DeepSHAP 计算出的每个输入时间序列 ${\mathbf{x}}_{t-\tau :t-1,j}$的重要性为 ${\varphi }_{ji}$。 通过将每个时间序列 j 的重要性值分配给 i，我们得到重要性矩阵 $\Phi$。 当我们设置HCG的稀疏度σ后，可以通过累积分布计算阈值γ，即$\gamma =F_{\varphi }^{-1}(\sigma ),$，其中如果我们假设所有的${\varphi }_{ji}$都是i.i.d，则$F_{\varphi }(\cdot )$是${\varphi }_{ji}$的累积分布。

利用先验知识提取 HCG。 某些领域的时间序列，例如天气或交通，每个变量之间的关系与几何距离高度相关。 例如，某个区域的空气质量或交通流量会在很大程度上影响附近区域的空气质量或交通流量。 因此，几何图可以作为这些领域的假设因果图（HCG），我们在Supp中展示了HCG计算过程。 A.2 节适用于本案例。

提取的 HCG 不是时间序列 X 的真实因果图，因为时间序列 X 不是由相应的 NAR 或 SCM 模型生成的（如图 2 所示）。 一个简单的解决方案是通过将非因果项的输入设置为零来运行自回归生成，即

其中 { h j i } \{h_{ji}\} {hji​}是HCG H中的条目。然而，方程中拟合模型$f_{{\Theta }_i}(\cdot )$的保真度 3 因仅包含变量的子集而受到阻碍。 下面，我们介绍另一种使用实际因果图生成时间序列的方法，最重要的是，不会失去保真度。

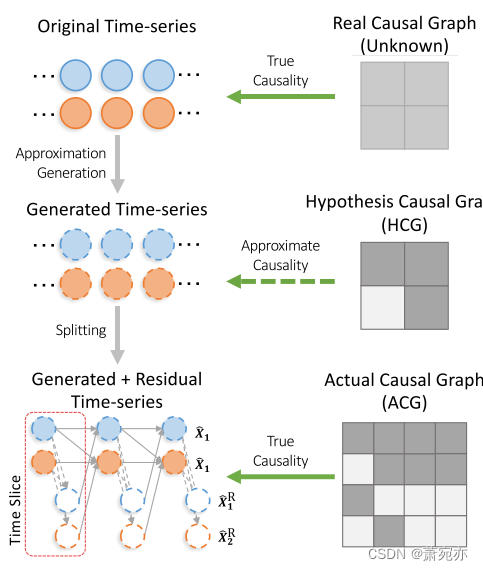
图 2：说明 CausalTime 如何获得精确合成所需数据的 2N × 2N 形状的稀疏因果图。

3.4 SPLITTING THE NAR MODEL TO ACQUIRE ACTUAL CAUSAL GRAPH AND REALISTIC TIME-SERIES拆分NAR模型以获得实际因果图和现实时间序列

为了获取实际因果图（ACG）并生成具有高数据保真度的新时间序列，我们建议将采用全连接预测模型形式的 NAR 模型拆分为因果项、残差项和噪声项。 这样，我们就不必在生成新的时间序列之前确定确切的因果关系，从而避免了“使用 TSCD 算法构建合成数据集来测试 TSCD 算法”的困境。 具体来说，

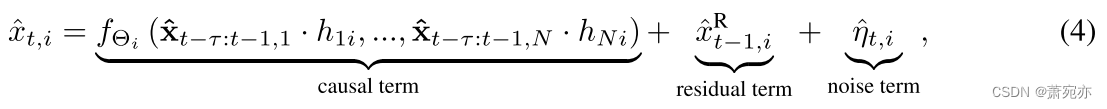
其中，残差项 ${\hat{x}}_{t-1,i}^{\mathrm{R}}$表示时间序列 i 的非父时间序列在 HCG H 中的“因果效应”。换句话说，因果项代表因果效应的“主要部分”，而 剩余项代表剩余部分。 数学上，${\hat{x}}_{t-1,i}^{\mathrm{R}}$计算为

然后存储为独立的时间序列。 然而，当被视为生成模型时，${\mathbf{x}}_j\to {\mathbf{x}}_i^{\mathrm{R}}$包含瞬时效应，这不会影响大多数现有 TSCD 方法的 ${\mathbf{x}}_j\to {\mathbf{x}}_i$的因果发现结果，正如我们在补充中讨论的那样。 A.1.2 节。 事实上，结合方程 4 和 5，${\mathbf{x}}_{t-1}$ 的所有分量都被包括来预测 ${\mathbf{x}}_t$，即“密集”预测模型。 然而，我们管道中的“密集”预测模型并不意味着“自然”因果图是密集的。 “自然”因果图的确切形式是未知的，因为我们不执行 TSCD。

从原始时间序列 X 中随机选择一个初始序列 ${\mathbf{X}}_{t_0-{\tau }_{\max }:t_0-1}$后，通过自回归模型生成 ${\mathbf{x}}_i$ 和 ${\mathbf{x}}_i^{\mathbf{R}}$，即前一个时间步的预测结果用于生成以下序列 时间步。 我们最终生成的时间序列包括所有${\mathbf{x}}_i$ 和 ${\mathbf{x}}_i^{\mathbf{R}}$，即总共生成 2N 个时间序列，$\text{ACG A}$ 的大小为 2N × 2N：
其中${\mathbf{J}}_N$是全一矩阵，${\mathbf{I}}_N$ 是单位矩阵，T 是生成的时间序列的总长度。 尽管原始时间序列的真实因果图未知，但对于生成版本，因果图是已知且唯一的，如图 2 所示。

通过预测模型$f_{{\theta }_i}$、归一化流模型$T_{{\psi }_i}$和ACG A，我们可以得到最终的数据集$⟨\hat{\mathbf{X}},\hat{\mathbf{A}}⟩$。 然后将$\hat{\mathbf{X}}$输入 TSCD 算法以恢复给定时间序列$\hat{\mathbf{X}}$ 的矩阵 A。

四、实验

在本节中，我们演示使用建议的管道构建的 CausalTime 数据集，可视化和量化生成的时间序列的保真度，然后在 CausalTime 上对现有 TSCD 算法的性能进行基准测试。

4.1 基准数据集统计

理论上，所提出的管道可以推广到不同的领域。 这里，我们分别根据天气、交通和医疗场景生成 3 种基准时间序列，如图 3 所示。对于天气和交通时间序列，两个变量之间的关系与其几何距离高度相关， 即，存在先验图，而医疗保健系列中没有这样的先验图。 详细的描述在Supp中。 A.2 节。

图 3：CausalTime 中三个子集的可视化。 对于 AQI 和交通流量，我们将地面实况因果图叠加到地图上。

4.2 生成时间序列的保真度

为了定性和定量分析生成的时间序列的保真度，我们利用 PCA Bryant & Yarnold (1995) 和 t-SNE van der Maaten & Hinton (2008) 降维可视化、基于神经网络的判别评分和 MMD 评分 真实和合成的特征向量来评估我们生成的时间序列是否真实。

通过降维进行可视化。 为了判断生成的时间序列的保真度，我们将时间序列特征投影到二维空间，并通过比较降维结果来评估它们的相似性。 将原始时间序列和生成的时间序列分割成短序列（长度为 5）后，我们通过线性（PCA）和非线性（t-SNE）方法对三个生成的数据集进行降维，并显式地可视化差异，如图 1 所示。 4. 可以观察到原始序列和生成序列的分布高度重叠，并且对于 AQI 和 Traffic 数据集（即第 1、2、4 和 5 列），相似性尤其突出。 这些结果直观地验证了我们生成的数据集在各个领域确实是真实的。

图 4：低维 (2D) 空间中生成的时间序列和原始时间序列之间相似性的可视化，其中原始序列和生成的序列分别以蓝色和红色显示。 (a) 和 (b) 在三个数据集上绘制了 PCA 和 t-SNE 的两个分量。

判别分数/MMD 分数。 除了低维空间中的可视化之外，我们还进一步评估生成质量，即使用基于神经网络的判别器和 MMD 分数定量评估原始时间序列和生成时间序列之间的相似性。 对于基于神经网络的判别器，通过将原始时间序列标记为正样本，将生成的时间序列标记为负样本，我们训练 LSTM 分类器，然后以 |AUROC − 0.5| 的形式报告判别分数。 在测试集上。 MMD 是评估两个分布相似性的常用指标（Gretton 等，2006）。 估计为${\widehat{\mathrm{MMD}}}_u^2=\frac{1}{n(n-1)}{\sum }_{i=1}^n{\sum }_{j\ne i}^{n}K(x_i,x_j)-\frac{2}{mn}{\sum }_{i=1}^n{\sum }_{j=1}^{m}K(x_i,y_j)+\frac{1}{m(m-1)}{\sum }_{i=1}^m{\sum }_{j\ne i}^{m}K(y_i,y_j)$，其中 K 是径向基函数 (RBF) 核。 MMD 给出了相似性的另一种定量评估，而无需训练另一个神经网络，如选项卡底行所列。 2. 观察到生成的数据集与原始数据集相似，因为判别得分非常接近于零（即神经网络无法区分生成的样本和原始样本），并且MMD得分相对较低。 除了判别分数和 MMD 之外，我们还利用互相关分数并进行加性实验，如 Supp 中所示。 A.3 节。

表 2：在判别得分和 MMD 方面对生成时间序列与原始时间序列之间的相似性进行定量评估。 我们也在表中显示了消融研究。

消融研究。 使用上述两个定量分数，我们还进行消融研究以证明我们设计的有效性。 在时间序列拟合中，我们使用归一化流来拟合噪声分布。 为了验证其有效性，我们用（a）加性高斯噪声（具有从真实序列估计的参数）和（b）无噪声来替换归一化流。 此外，为了验证我们的管道通过将因果模型分为因果项、残差项和噪声项来保留真实动态，我们在 © 拟合 NAR 模型或 (d) 时添加了两种不包括残差项的替代方案 除了上述两个设置外，还可以生成新数据。

结果如表所示。 图 2 表明，完整模型生成的时间序列在判别得分和 MMD 得分方面都最好地模仿了原始时间序列。 唯一的例外是医学数据集“无噪声”设置下的 MMD 略低。 值得注意的是，我们的辨别分数接近于零，即神经网络无法区分几乎所有生成的时间序列与原始版本。

4.3 最先进的因果发现算法的性能

为了量化不同因果发现算法的性能，我们在这里计算它们相对于真实因果图的 AUROC 和 AUPRC。 我们不评估所发现的因果图 $\tilde{\mathbf{A}}$ 相对于其真实值 $\hat{\mathbf{A}}$的准确性，因为 ${\mathbf{x}}_j\to {\mathbf{x}}_i^{\mathrm{R}}$中存在瞬时效应（参见补充部分 A.1.2）。 相反，我们忽略等式中的 ${\mathbf{I}}_N,{\mathbf{J}}_N$ 和 0 块。 6), 并将$\tilde{\mathbf{H}}$与 H 进行比较，

基线 TSCD 算法。 我们在 CausalTime 数据集上对 13 种最近或有代表性的因果发现方法的性能进行了基准测试，包括：i) 基于格兰杰因果关系的方法：格兰杰因果关系（GC，（Granger，1969））、神经格兰杰因果关系（NGC，（Tank 等人） ., 2022))、经济 SRU (eSRU, (Khanna & Tan, 2020))、可扩展因果图学习 (SCGL, (Xu et al., 2019))、时间因果发现框架 (TCDF, (Nauta et al., 2019)) , 2019))、CUTS (Cheng et al., 2023b)、CUTS+ (Cheng et al., 2023a) 将 CUTS 升级到高维时间序列。 ii) 基于约束的方法：PCMCI（Runge 等人，2019b）、SVAR、NTS-NOTEARS（显示为 N.NTS，（Sun 等人，2023））和 Rhino（Gong 等人，2022）， iii) 基于 CCM 的方法：潜在收敛交叉映射（LCCM，（Brouwer 等人，2021）），以及 iv）其他方法：神经图形模型（NGM，（Bellot 等人，2022）），它采用神经普通模型 处理不规则时间序列数据的微分方程。 为了确保公平性，我们在验证数据集上为这些基线算法搜索最佳超参数集，并在每个实验 5 个随机种子的测试集上测试性能。

表 3：我们的 CausalTime 数据集上的基线 TSCD 算法的性能基准测试。 我们分别用粗体和下划线突出显示最好的和第二好的。
结果与分析。 从表中的分数来看。 从图3可以看出，在这些算法中，CUTS+和LCCM表现最好，而大多数TSCD算法的AUROC都没有> 0.9。 较低的精度表明，当前的 TSCD 算法距离实际应用还有很长的路要走，也表明有必要设计更先进的、对实际数据具有较高可行性的算法。 有趣的是，一些结果表明 AUROC < 0.5，这意味着我们得到了反向分类。 PCMCI 等基于约束的方法在合成数据集（尤其是线性情况，(Cheng et al., 2023b)）上实现了高性能，但在实际数据上表现较差。 这可能是由于在非线性或现实场景中进行条件独立性测试很困难。 基于格兰杰因果关系的方法（例如 CUTS+）由于其基于神经网络的架构而表现最佳。 然而，这些方法（例如 CUTS、CUTS+、NGC、eSRU）具有局限性，因为它们依赖于因果充分性的假设并且没有瞬时影响。 基于 CCM 的方法 LCCM 的表现出人意料地好，尽管在合成数据集中表现不佳（Cheng 等人 (2023b) 中报告）。 这证明学习基于NeuralODE的潜在过程极大地有助于Convergent Cross Mapping的应用。 此外，与之前工作中报告的结果（Cheng et al., 2023b; Tank et al., 2022）相比，我们可以注意到我们的 CausalTime 数据集上的分数明显低于合成数据集（例如 VAR 和 Lorenz）上的分数。 -96），一些 TSCD 算法的得分接近 1。这意味着现有的合成数据集不足以评估真实数据上的算法性能，需要建立新的基准来推动该领域的发展。

附加信息。 我们将理论分析和假设放在补充材料中。 A.1 节，A.2 节中每个关键步骤的实现细节以及超参数，其他实验结果（包括各种 CDNN 实现的比较、计划采样的消融研究以及互相关分数和与 A.3 节中的缺失条目或混淆），以及第 1 节中的算法表示。

五、结论

我们提出了 CausalTime，一种新颖的管道，用于生成具有真实因果图的真实时间序列，可用于评估 TSCD 算法在真实场景中的性能，也可以推广到不同领域。 我们的 CausalTime 通过在不同的现实设置下实现升级的算法评估来为因果发现社区做出贡献，这将促进 TSCD 算法的设计和应用。 我们的工作可以在多个方面进一步发展。 首先，用SCM模型替代NAR可以将CausalTime扩展到更丰富的因果模型集合； 其次，我们计划考虑现实时间序列中广泛存在的多尺度因果效应。 我们未来的工作包括 i) 通过结合某些动态过程、多尺度关联或瞬时效应的先验知识来创建更真实的时间序列。 ii) 研究增强的 TSCD 算法，在实时序列数据上获得可靠的结果。

A.1 理论

A.1.1 假设和限制

CausalTime 是测试各种 TSCD 算法的现实基准。 因此，我们选择包括最常见的假设，例如马尔可夫条件、因果忠实性、无瞬时效应、因果充分性和因果平稳性。

马尔可夫条件。 联合分布可以分解为 $P(\mathbf{x})={\prod }_{i}P(x_i|\mathcal{P}(x_i))$，即每个变量都独立于其所有非后代，并以其父代为条件。

因果忠诚。 准确反映数据中存在的独立关系的因果模型。

因果充分性。 （或没有潜在的混杂因素）观察到所有变量的所有常见原因。 这个假设可能非常强大，因为我们无法观察“世界上的所有原因”，因为它可能包含无限变量。 然而，这个假设对于各种文献都很重要。

无瞬时效果。 （或时间优先级（Assaad et al., 2022））在时间序列中，原因发生在其结果之前。 如果采样频率高于因果效应，则可以满足该假设。 然而，这个假设可能很强，因为许多实时时间序列的采样频率不够高。 在 CausalTime 中，测试了支持瞬时效果的方法，例如 Rhino 和 DYNOTEARS Kong 等人。 （2022）； 帕姆菲尔等人。 通过仅测试滞后部分，（2020）仍然是可能的。 然而，我们无法测试瞬时部分，这确实是一个限制。

因果平稳性。 所有因果关系始终保持不变。 有了这个假设，全时因果图可以概括为窗口因果图（Assaad et al., 2022）。

在AQI和Traffic数据集中，因果关系与几何距离高度相关，因为附近的站点具有相互影响，因此提取的HCG和后续的ACG直接来自距离图，这符合常识并被广泛使用Cini等人。 （2022）； 吴等人。 （2019）。 在医学数据集中，HCG 是使用 DeepSHAP 提取的，因为仅根据先验知识很难构建可靠的图表。 尽管 Shapley 值可能与因果关系不完全匹配，但基于 Shapley 值的方法广泛应用于医学领域，并且被证明可以捕获具有实际重要关系的特征 Hyland 等人。 （2020）； 托森-迈耶等人。 （2020）。 因此，我们三个子集中提取的图表是建立在现有的广泛研究的基础上的，预计与自然界中发现的图表接近。

A.1.2 剩余期限的瞬时效应

在第 3.4 节中，我们建议将 NAR 模型分为因果项、残差项和噪声项，其中残差项 $x_{t-1}^{\mathrm{R}}$生成为

因此，该生成方程中存在瞬时效应，即在${\mathbf{x}}_j\to {\mathbf{x}}_i^{\mathrm{R}}$中，但在 ${\mathbf{x}}_j\to {\mathbf{x}}_i,\forall i,j.$ 中不存在。 在与瞬时效果兼容的 TSCD 算法上进行测试时，这不是问题。 接下来，我们讨论在不兼容瞬时效应的 TSCD 算法上进行测试时的后果，例如格兰杰因果关系、收敛交叉映射和 PCMCI（Runge 等人，2023）。 对于大多数情况，这不会影响所有 ${\mathbf{x}}_j$之间的因果发现结果。 尽管他们可能会得出 xj ↛ xR i 的错误结论，但这不是我们在评估中与真实情况进行比较的部分（第 4.3 节）。

Granger Causality 格兰杰因果关系通过测试一个时间序列是否有助于预测另一个时间序列来确定因果关系。 在这种情况下，${\mathbf{x}}_j\to {\mathbf{x}}_i$的因果发现结果不受影响，因为 ${\mathbf{x}}_j\to {\mathbf{x}}_i^{\mathrm{R}}$的瞬时效应不会影响时间序列 $x_j$ 是否有助于预测时间序列 $x_i$, ∀i, j。

基于约束的因果发现。 这些工作基于条件独立性测试，即，如果 ${\mathbf{x}}_{t_0,j}\to {\mathbf{x}}_{t,i}$，则 x t 0 , j ⊥̸ x t , i ∣ X t − τ : t − 1 \ { x t 0 , j } x_{t_{0},j}\not\perp x_{t,i}|\mathbf{X}_{t-\tau:t-1}\backslash\{x_{t_{0},j}\} xt0​,j​⊥xt,i​∣Xt−τ:t−1​\{xt0​,j​}，其中$t-\tau \le t_0<t$（Runge 等人，2019b；Runge，2020）。 当考虑$x_{t,j}\to x_{t,i}^{\mathrm{R}},$的瞬时效应时，这种关系不受影响，因为从 $x_{t_0,j}$到 $x_{t,i}$通过 $x_{t,k}^{\mathrm{R}}$的所有路径都被 $x_{t,k}^{\mathrm{R}}$, ∀i, j, k 的条件阻止 ，如图5所示。

图 5：${\mathbf{x}}_j\to {\mathbf{x}}_i^{\mathrm{R}}$的瞬时效应图示。 从 $x_{t_0,j}$到 $x_{t,i}$通过 $x_{t,k}^{\mathrm{R}}$ 的所有路径都通过 $x_{t,k}^{\mathrm{R}}$, ∀i, j, k 的条件来阻止。

A.1.3 生成的时间序列中的因果关系

CausalTime 的目的是生成时间序列 (i) 具有用于基准测试的独特的地面真实因果图，以及 (ii) 与真实数据的分布高度相似，用于评估算法在真实数据上的性能。 我们通过三个步骤来实现这一目标：

1. 3.3节中提取HCG。 这里的 HCG 并不是真实的因果图，因为它只反映了因果关系的“主要部分”。
2. 将 NAR 模型拆分为因果项、残差项和噪声项。 这里因果项也代表因果关系的“主要部分”，剩余项代表其余部分。
3. 将残差项 ${\hat{x}}^{\mathrm{R}}$ 视为独立的时间序列。 结果，存在 2N 个而不是原来的 N 个时间序列。 并且图（ACG）变为2N×2N，如式（1）所示。 6. 该过程如图 2 所示。

通过这种方式，我们可以确保${\hat{x}}_{t,i}$仍然是由原始 NAR 模型生成的，因为结合方程 6 和 7，我们得到了原始的 NAR 形式。 此外，ACG 是真实因果图，因为我们将残差项 ${\hat{x}}^{\mathrm{R}}$as 视为独立的时间序列。 因此，原始时间序列的真实因果图是未知的，但对于生成的版本，因果图是已知且唯一的，即 ACG。 这样，我们就避免了“使用 TSCD 算法构建合成数据集来测试 TSCD 算法”的困境。 我们在图 2 中展示了这种关系。

A.2 实施细节

原始时间序列。 在 CausalTime 中，我们分别根据天气、交通和医疗保健场景生成 3 种基准时间序列。 原始时间序列为 1. 空气质量指数 (AQI) 是分布在中国城市 2 的 36 个监测站的多个空气质量特征的子集，在一年内每小时进行一次测量。 我们考虑数据集中的 PM2.5 污染指数。 数据集的总长度为 L = 8760，节点数量为 N = 36。我们通过计算传感器之间的成对距离来获取先验图（补充部分 A.2）。 2. 交通子集是根据旧金山湾区交通传感器收集的时间序列构建的。 数据集的总长度为 L = 52116，我们包括 20 个节点，即 N = 20。先前的图也是根据地理距离计算的（补充 A.2 节）。 3. 医疗子集来自 MIMIC-4，该数据库为重症监护病房超过 40,000 名患者提供重症监护数据（Johnson 等，2023）。 我们从 1000 名患者中选择了 20 个最常测试的生命体征和“图表事件”，然后将其转换为时间序列，其中每个时间点代表 2 小时的间隔。 使用最接近的插值来估算缺失的条目。 对于该数据集，由于极其复杂的动态，无法获得先验图。

网络结构和培训。 CDNN 的实现可能有所不同，cMLP / cLSTM 不是唯一的选择。 例如，程等人。 (2023a) 探索通过基于消息传递的神经网络增强因果发现，这是具有广泛权重共享的 CDNN 的特殊版本。 然而，CDNN 的拟合精度研究较少。 共享部分权重可以缓解结构冗余问题。 此外，最新结构的性能未知，例如 变压器。 接下来，这项工作研究了 CDNN 应用于拟合因果模型时的各种实现。 具体来说，应用了结合三种网络共享策略的三种骨干网，即MLP、LSTM、结合不共享的Transformer、共享编码器和共享解码器。 对于MLP，编码器和解码器都是MLP。 对于 LSTM，我们分配一个 LSTM 编码器和一个 MLP 解码器。 对于 Transformer，我们分配一个 Transformer 编码器和 MLP 解码器。 我们通过一个三变量示例在图 6 中展示了无共享、共享编码器和共享解码器的结构。 使用这些架构进行预测的测试结果如表 1 所示。 6.

图 6：CDNN 的网络结构示意图。

---