【SCI】【分数阶极值寻优控制】极值寻优控制（ESC）的新的最大功率点跟踪（MPPT）研究（Simulink仿真实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

极值寻优控制（ESC）的新的最大功率点跟踪（MPPT）研究

一、引言

二、分数阶极值寻优控制原理

三、MPPT技术概述

四、分数阶ESC在MPPT中的应用

五、仿真实验与结果分析

六、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Simulink仿真、文章

---

💥1 概述

在这个模拟中，采用了一种名为"极值寻优控制（ESC）"的新的最大功率点跟踪（MPPT）方法来寻找光伏系统的峰值功率点。经过良好调整的ESC与其他MPPT算法（如P&O或IC）相比具有更高的效率。

参考文献：

在本论文中，分析并对比了一种新颖的极值寻优控制算法，称为分数阶极值寻优控制，与传统的整数阶算法进行了基准测试。在极值寻优方案中利用分数阶算子能够提高该方法的收敛速度、鲁棒性和性能，而无需额外的模块。通过采用平均模型，详细分析了分数阶极值寻优控制。仿真和实验结果支持了数学分析，并表明所提出的方案优于传统的极值寻优算法。

极值寻优控制（ESC）是一种在线自适应算法，旨在实时确定未知非线性性能函数的极值（最大值或最小值），从而通过消除离线数据分析的需求来减少停机时间。这种极值寻优方法已成功应用于广泛的电机工程应用中，包括可再生能源系统中的最大功率点跟踪，ABS刹车控制，燃烧发动机时序控制，移动机器人路径规划等。关于ESC及其应用的描述性调查可在文献[16]和[17]中找到。

由于工程应用的广泛范围，研究人员和科学家对通过提供更好的微调和校准方法来改进该算法的性能和可靠性表现出越来越浓厚的兴趣。Nesic在文献[18]中提出了调节指南，可以确保极值寻优算法具有更大的吸引域和更快的收敛速度。Nesic [18]声称，在适当调节ESC参数的情况下，全局峰值将在局部极值存在的情况下被实现。Moura和Chang [3]以及Ghods [14]通过在反馈环路中添加动态补偿来改进了这一算法，以增加收敛速度。

极值寻优控制（ESC）的新的最大功率点跟踪（MPPT）研究

一、引言

极值寻优控制（ESC）是一种在线自适应算法，旨在实时确定未知非线性性能函数的极值（最大值或最小值），从而通过消除离线数据分析的需求来减少停机时间。近年来，ESC在可再生能源系统中的最大功率点跟踪（MPPT）方面得到了广泛关注。本文探讨了基于分数阶极值寻优控制的ESC方法，以提高光伏系统MPPT的效率。

二、分数阶极值寻优控制原理

分数阶极值寻优控制是在传统的整数阶极值寻优控制基础上发展而来的。通过在极值寻优方案中利用分数阶算子，能够提高方法的收敛速度、鲁棒性和性能，而无需额外的模块。分数阶ESC的核心在于其分数阶导数或积分的运算，这使得算法在应对复杂非线性系统时具有更强的适应性和灵活性。

三、MPPT技术概述

最大功率点跟踪（MPPT）技术是光伏系统中的重要组成部分。它通过不断调整光伏组件的工作电压，从而追踪并保持在最大功率点上，以确保光伏组件在各种光照条件下都能以最高的效率进行发电。MPPT技术的实现主要依赖于DC-DC变换电路，该电路能够将固定的直流电压转换为可调节的直流电压，从而为跟踪最大功率点提供技术支持。

四、分数阶ESC在MPPT中的应用

在光伏系统的MPPT中，分数阶ESC通过实时监测光伏组件的发电电压和电流，利用分数阶算子对电压进行调整，以实现最大功率点的追踪。相较于传统的整数阶ESC算法，分数阶ESC具有更快的收敛速度、更高的鲁棒性和更优的性能。此外，分数阶ESC还能够在局部极值存在的情况下实现全局峰值，从而提高了MPPT的准确性和可靠性。

五、仿真实验与结果分析

为了验证分数阶ESC在MPPT中的有效性，本文进行了Simulink仿真实验。实验结果表明，分数阶ESC算法在收敛速度和性能上均优于传统方法。在相同的光照条件下，分数阶ESC能够更快地找到最大功率点，并保持稳定。此外，分数阶ESC还能够在光照条件发生变化时迅速调整工作电压，以实现最大功率点的重新追踪。

六、结论与展望

本文探讨了基于分数阶极值寻优控制的ESC方法在光伏系统MPPT中的应用。通过Simulink仿真实验，验证了分数阶ESC在收敛速度、鲁棒性和性能上的优势。未来研究可以进一步探索分数阶ESC的优化策略、与其他智能算法的融合以及在实际光伏系统中的应用效果评估等方面，以推动MPPT技术的不断发展和创新。

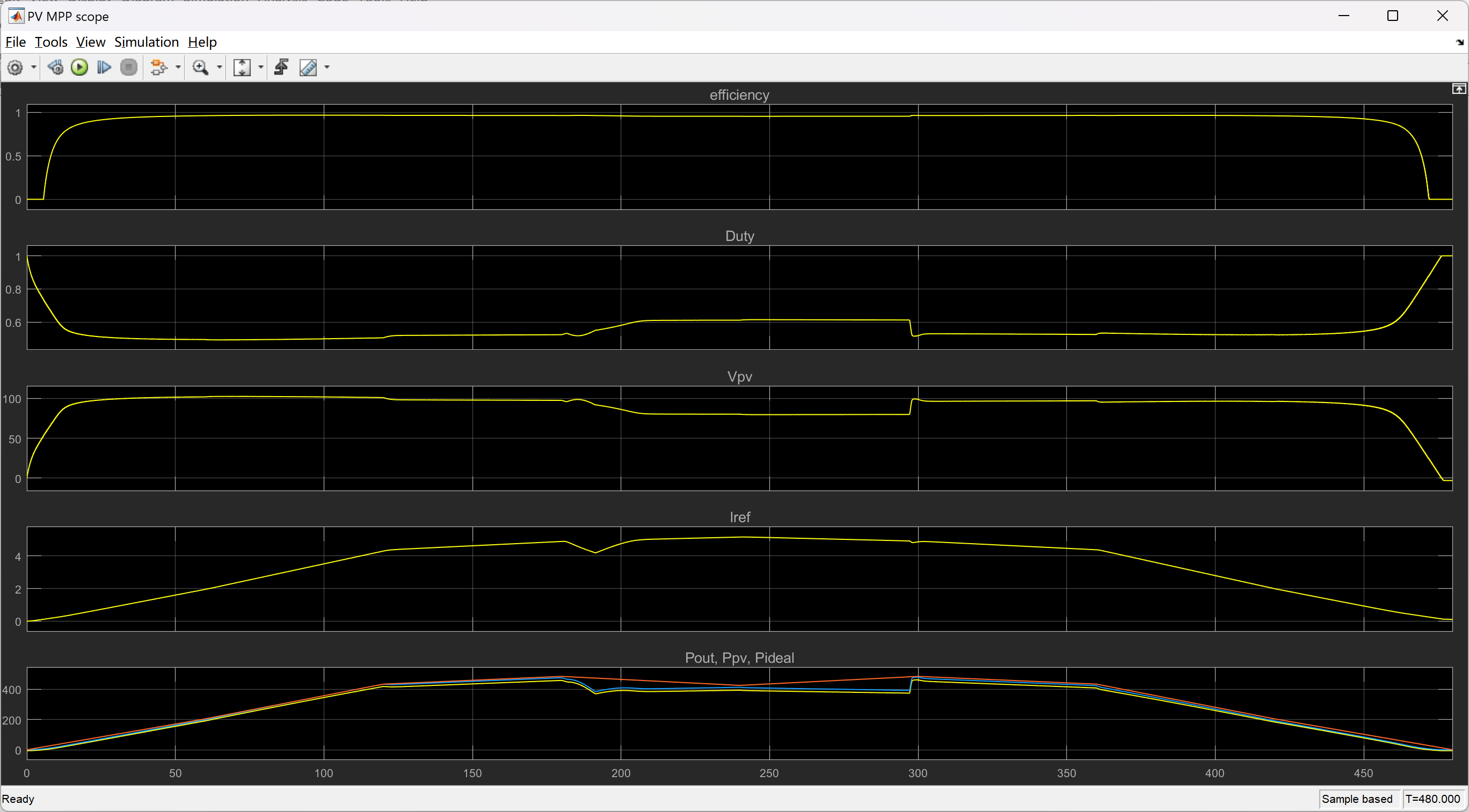
📚2 运行结果

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

1- H. Malek; S. Dadras; Y. Chen, "Performance analysis of fractional order extremum seeking control", ISA Transactions, Vol 16, doi: 10.1016/j.isatra.2016.02.024.
2- H. Malek; Y. Chen, "Fractional Order Extremum Seeking Control; Performance and Stability Analysis", IEEE/ASME Transactions on Mechatronics, doi: 10.1109/TMECH.2016.2517621.

🌈4 Simulink仿真、文章