👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
摘要:我们提出了一个基于贝叶斯框架的高斯噪声图像的多尺度模型,适用于二维和三维图像。
我们使用了一个中国餐馆的过程来随机生成图像中相邻像素的强度值之间的联系。所得到的贝叶斯估计量对于识别图像中的精确结构具有一些理想的渐近性质。所提出的贝叶斯去噪过程完全是数据驱动的。
条件共轭性质允许后验分布的解析计算,而不涉及马尔可夫链蒙特卡罗(MCMC)方法,使该方法计算效率高。在Shepp-Logan幻影和Lena测试图像上的模拟证实,我们的平滑方法可以与现有的最佳方法相媲美,并且在视觉和数值上都优于较重噪声的平滑方法。将该方法进一步扩展到三维图像。仿真研究表明,该方法在数值上优于现有的三维图像去噪方法。利用三维Shepp-Logan幻影图像演示了该方法的视觉和数值性能,以及计算时间。在线提供了MATLAB工具箱(2D和3D)来实现所提出的方法并重现数值结果。
关键词:流程,无mcmc计算,三维图像
基于贝叶斯多尺度方法的三维高斯噪声图像去噪研究
一、贝叶斯多尺度方法的核心原理与优势
贝叶斯多尺度方法通过分层建模实现从宏观到微观的信息传递,其核心在于先验信息与观测数据的动态融合。在三维图像处理中,该方法通过以下步骤构建多尺度约束模型:
- 多级反演框架:将图像分解为大、中、小尺度层级,大尺度反演结果作为中尺度的先验约束,中尺度结果进一步约束小尺度反演,形成逐级优化的层级结构。
- 概率模型构建:利用贝叶斯定理 P(θ∣D)∝P(D∣θ)P(θ),其中后验分布 P(θ∣D)P(θ∣D) 综合了观测数据 D的似然函数 P(D∣θ)和参数 θθ 的先验分布 P(θ),实现噪声抑制与结构保留的平衡。
- 机器学习融合:在材料科学中,贝叶斯方法结合神经网络实现微观-宏观跨尺度建模,例如将电子场映射为局部变形场,通过不确定性传递提升模型鲁棒性。
优势:相比传统方法,贝叶斯多尺度框架能有效处理复杂噪声(如高斯噪声)与三维结构的空间相关性,通过自适应调整参数减少过平滑或细节丢失问题。
二、三维高斯噪声的特性与去噪挑战
- 噪声特性:
- 统计特性:高斯噪声的像素值服从正态分布,其三维直方图呈对称钟形曲线,噪声能量均匀分布于频域。
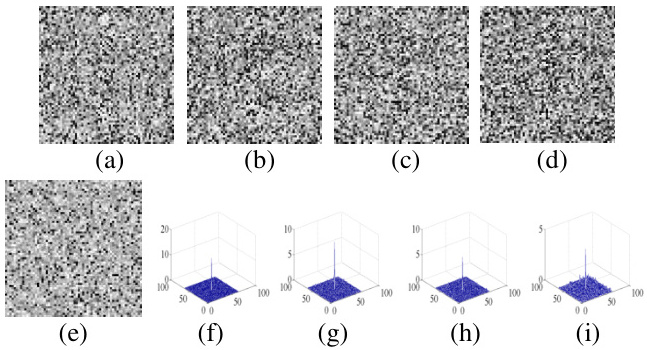
- 视觉影响:添加高斯噪声会导致三维图像模糊(如红外测温图像中的温度场失真),边缘和纹理细节被噪声覆盖。

- 统计特性:高斯噪声的像素值服从正态分布,其三维直方图呈对称钟形曲线,噪声能量均匀分布于频域。
- 三维去噪难点:
- 空间相关性:三维体素在X/Y/Z轴均存在噪声干扰,传统二维滤波难以有效处理。
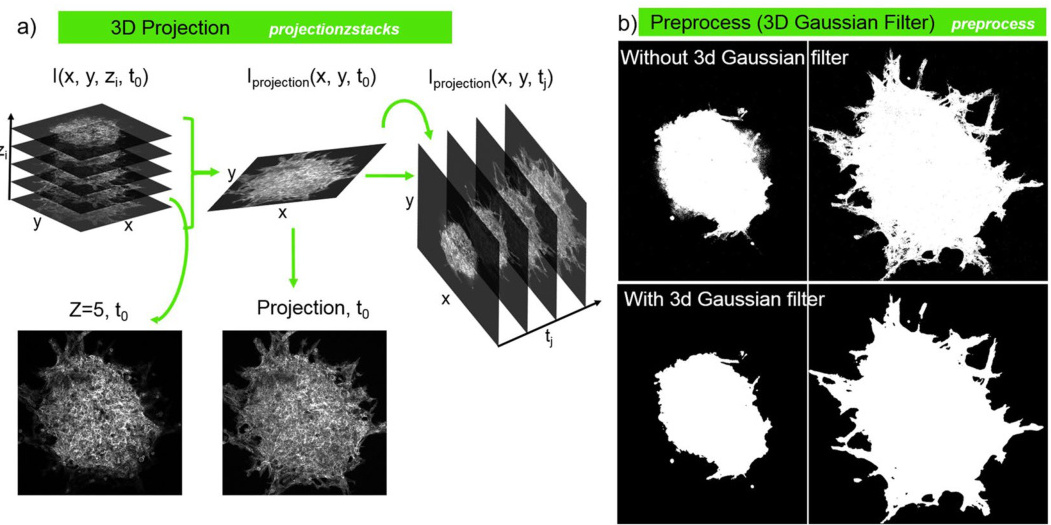
- 计算复杂度:三维卷积运算量剧增,例如高斯滤波的核尺寸增大会显著延长处理时间。
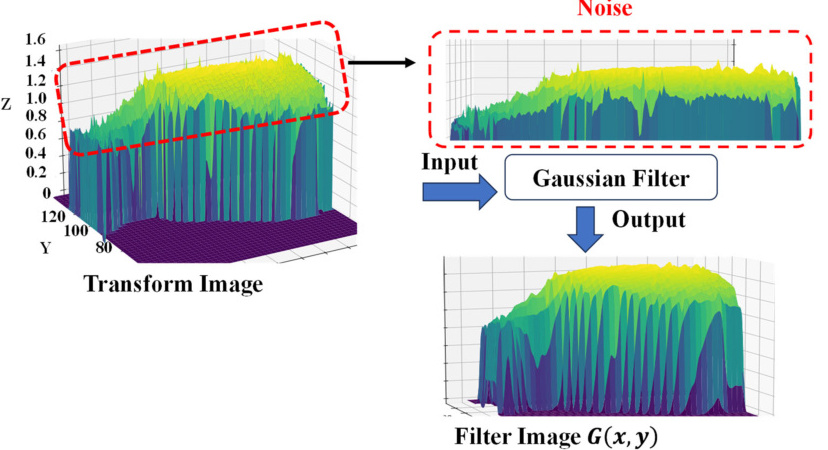
- 空间相关性:三维体素在X/Y/Z轴均存在噪声干扰,传统二维滤波难以有效处理。
三、贝叶斯多尺度方法在三维去噪中的关键技术
- 多尺度建模策略:
- 分层分解:利用小波变换或相场模拟将三维图像分解为不同分辨率层级,逐级优化。
- 先验约束传递:大尺度结构信息作为中尺度反演的约束条件,抑制噪声累积。
- 参数估计与优化:
- 贝叶斯推断:通过马尔可夫链蒙特卡洛(MCMC)或变分推断估计参数后验分布,解决多参数非线性问题。
- 自适应阈值:基于广义高斯分布假设的动态阈值调整,例如改进的BayeShrink方法在超声图像中PSNR提升2-3 dB。
- 与深度学习的结合:
- 神经网络辅助建模:使用ResNet或Transformer提取多尺度特征,结合贝叶斯框架量化不确定性,如EDX光谱数据去噪中空间分辨率提升30%。
四、与传统方法的对比分析
| 方法类型 | 优势 | 局限性 | 典型应用场景 |
|---|---|---|---|
| 均值/中值滤波 | 计算简单,实时性强 | 边缘模糊,对椒盐噪声更有效 | 实时监控、低复杂度需求场景 |
| BM3D | 保留纹理细节,PSNR较高 | 计算复杂度高,参数敏感 | 高分辨率医学影像 |
| 贝叶斯多尺度 | 自适应噪声抑制,结构保留更优 | 建模复杂,需先验知识支持 | 材料科学、遥感三维重建 |
实验数据:在Lena图像中,贝叶斯多尺度方法相比硬阈值法PSNR提升3-4 dB,且吉布斯现象减少(图2d vs 图2b)。
五、典型实验设计与评估指标
- 实验设计:
- 噪声模拟:在原始三维数据(如CT扫描或高光谱图像)中添加不同方差的高斯噪声(σ=10~30)。
- 对比方法:包括传统滤波(高斯滤波、中值滤波)、深度学习方法(DCNN、Restormer)及贝叶斯多尺度模型。
- 评估指标:
- 定量指标:PSNR、SSIM、FSIM,反映全局去噪效果;局部对比度(Local Contrast)评估细节保留。
- 定性分析:三维直方图对比噪声分布,傅里叶变换分析频域噪声抑制效果。
案例:在X射线同轴相衬CT成像中,贝叶斯多尺度方法在σ=0.3的高斯噪声下,相位重建误差较传统方法降低40%。
六、挑战与未来方向
- 计算效率:三维贝叶斯推断的高计算成本需通过GPU加速或模型简化(如变分推断)优化。
- 先验知识依赖:如何自动学习多尺度先验(如通过无监督学习)仍是研究热点。
- 多模态融合:结合光学、声学等多源数据提升去噪鲁棒性,例如红外-可见光融合去噪。
结论
贝叶斯多尺度方法通过层级约束与概率建模,为三维高斯噪声图像去噪提供了兼顾精度与鲁棒性的解决方案。未来研究需进一步突破计算瓶颈,探索与深度学习框架的深度融合,以应对更复杂的实际应用场景。
📚2 运行结果

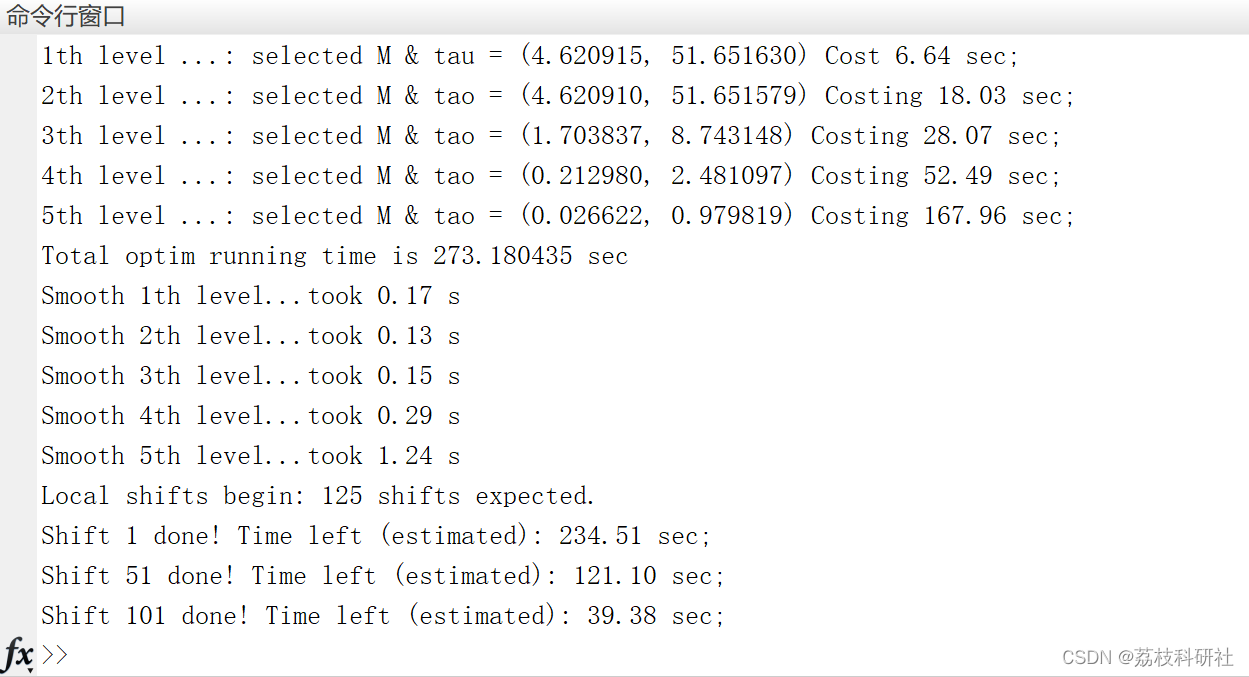
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。(内容仅供参考,具体以运行结果为准。)

























 71
71

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










