扩增子分析|NST包-随机性过程、确定性过程的相对贡献之应用篇（NST变式MST和pNST及代码实例）

最新推荐文章于 2025-05-03 10:20:22 发布

清同趣科研

最新推荐文章于 2025-05-03 10:20:22 发布

阅读量995

点赞数 33

分类专栏： R绘图基础微生物群落构建机制文章标签： r语言算法

本文链接：https://blog.csdn.net/weixin_46814750/article/details/145394954

版权

R绘图基础同时被 2 个专栏收录

12 篇文章

订阅专栏

微生物群落构建机制

7 篇文章

订阅专栏

by Tom Dingyan Zhang

一、引言

关于NST包的推出和应用已经有一段时间了。在上一节，我们阐述了NST原理部分，详细内容可跳转至NST包|从原理到应用，教你理解群落组装机制中随机性过程、确定性过程的相对贡献（数学公式、表现性能详细介绍）学习探讨。本节紧接上节探讨NST的变式以及各种NST计算方法和代码实例。

二、NST的变式

在关于NST的论文中作者提到，NST有多种变式，除了前文介绍的基于物种的taxonimic NST(tNST)外，还有基于系统发育零模型的phylogenetic NST(pNST)，以及经过算式调整的modified NST(MST)。这些指数也都出现在了Oklahoma的研究者论文当中。同时，有许多研究论文中都采用了这种方法。

2.1 关于MST(Modified Stochasticity Ratio)

这里的MST是对tNST进行修正。这一方法最早出现在梁玉婷老师的文章1中，给出了系统的公式，并且这一公式比tNST表现出了更好的效果。

MST相对于NST来说，计算公式更加简单粗暴。然而其通用性有了一定提高。

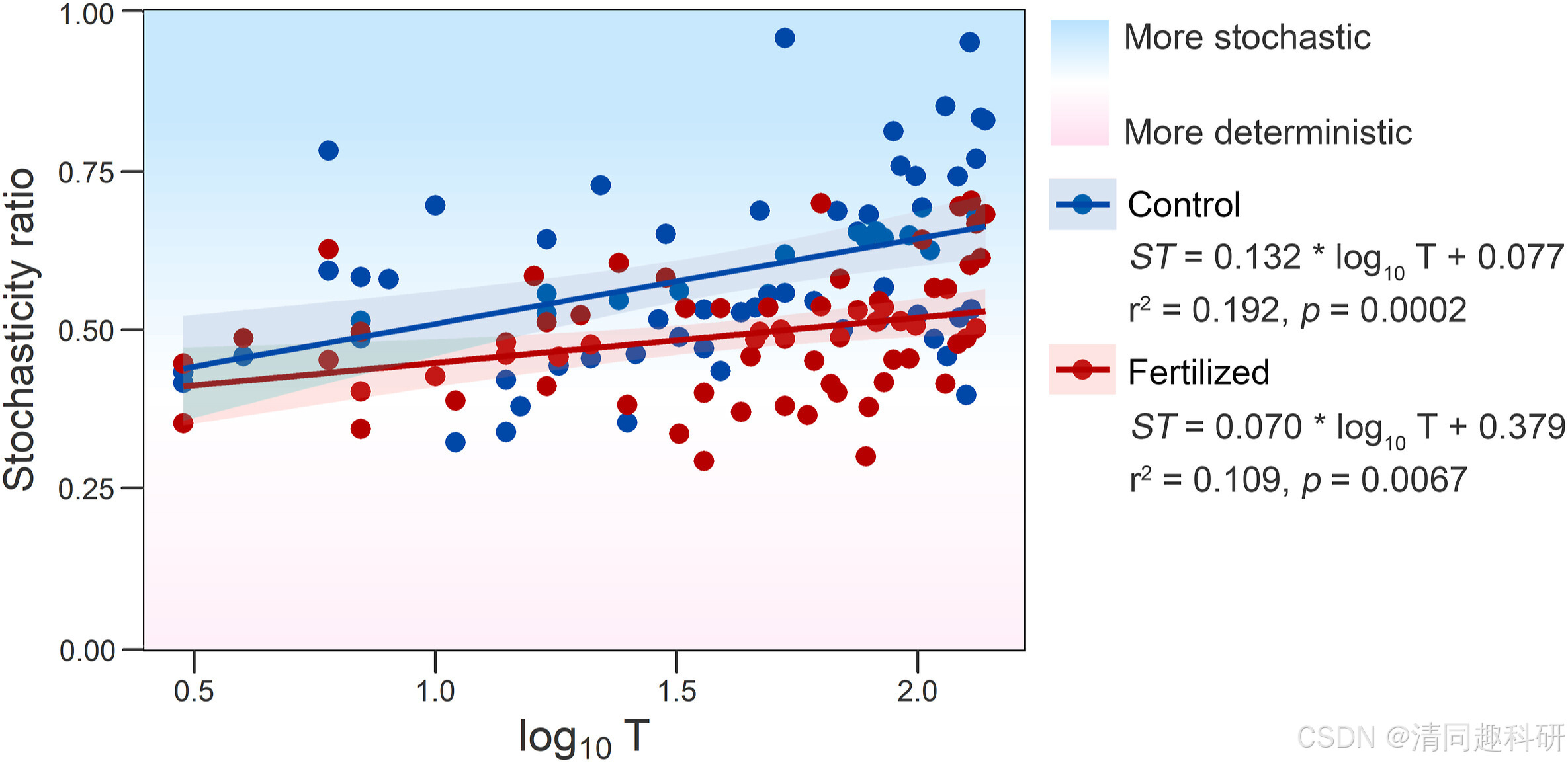
图1：随机比率随时间对数的变化

由图可得，对照组和施肥组的草原土壤中的微生物随时间演替的趋势，都是随机性过程的贡献显著升高。但是，施肥会使得随机性过程贡献升高的速度变慢。

2.2 关于pNST

前身：2018年郭雪老师2

图2：群落微生物在常温和变暖环境下的组装过程随机性差异

图片表明，无论基于分类学多样性(a)还是系统发育多样性(b)，在变暖条件下，细菌和真菌的群落组装过程中的随机性占比都会显著降低。

这篇文章是最先使用系统发育距离进行随机比率计算的文章，里面呈现的方法，算是pNST的前身。图b表示的是基于系统发育β多样性指数βMNTD计算出的随机比率。这背后的原理很简单，当NTI位于[-2,2]之间，就可以认为生态过程是随机的，随后根据位于此区间内的成对样本点数来计算随机比。

发表与测试：2020年宁老师3

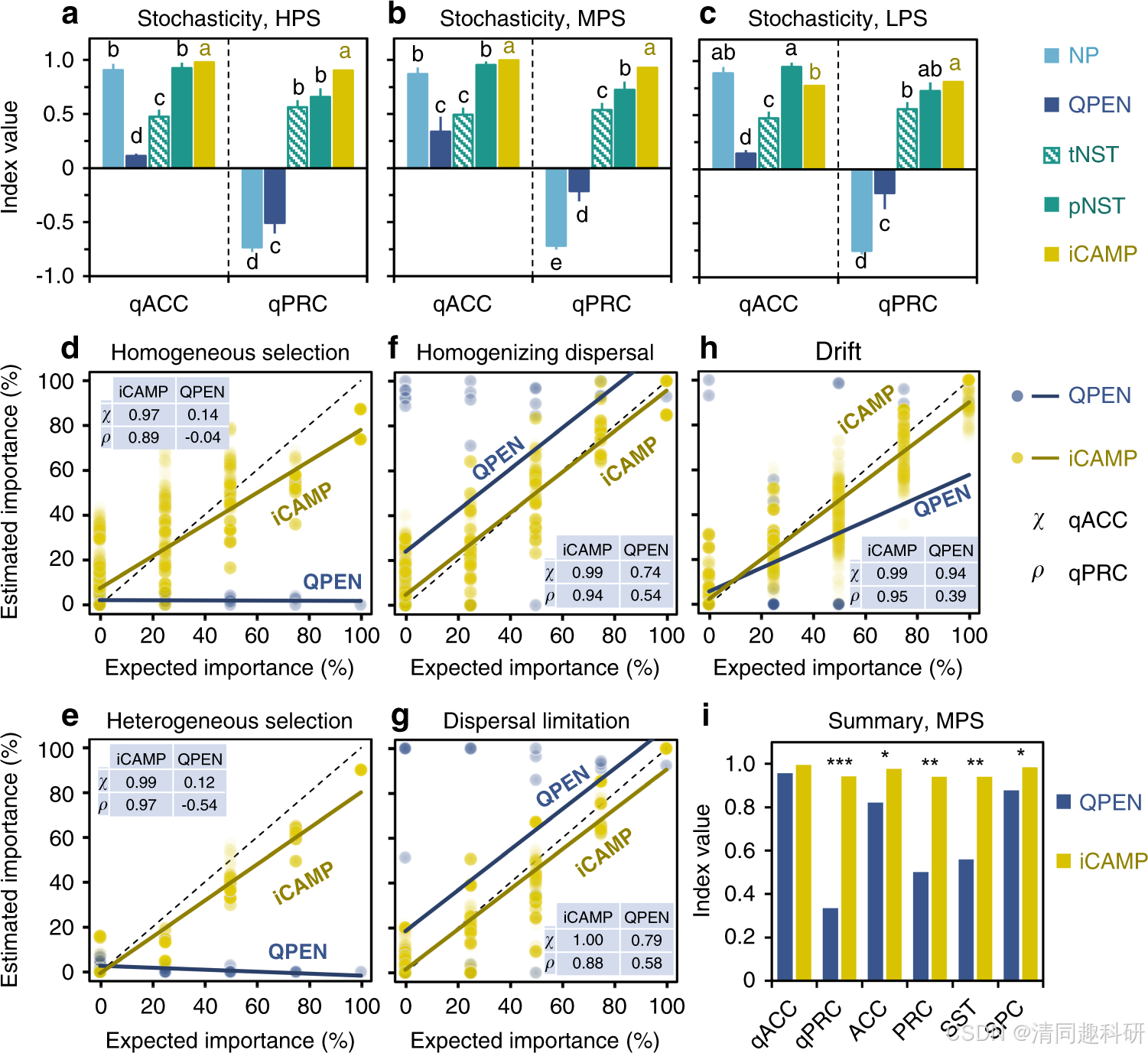
图3：iCAMP与其他主流模型方法的预测结果对比

通过模拟群落实验，来得到各个模型的定量结果，以定量准确度(qACC)和精确度(qPRC)来评估性能。结果表明，在模拟低、中、高三个系统发育信号强度的情况下，pNST都显示出比tNST更加优秀的预测精准度，与iCAMP的预测最接近。

根据我本人初步解码NST包中的pNST函数，可以得到一些有效信息：首先，pNST的计算底层逻辑是基于了系统发育零模型，与βMNTD和βNTI相关，而这是Stegen等人论文中的理论4。但是pNST能够超出经典的QPEN零模型框架，得到更好的预测结果，自然不可能仅仅是将早期的理论拿来套用。为了弄清里面的机制，我进一步分析了该包的原代码。其中，有一段是这么写的：

  rand.amax = apply(dist.ran, 1, max)
  rand.bmax = apply(dist.ran, 1, function(v) {
    max(stats::density(v)$x)
  })
  d.up1 = (sum((obs <= 1) * (rand.amax <= 1)) == length(obs)) * 
    (rand.bmax > 1)
  rand.max = d.up1 + ((1 - d.up1) * rand.bmax)
  Dmax = max(obs, rand.max)
  GD = rand.mean/cbind(dist.ran, obs)
  EC = (Dmax - rand.mean)/(Dmax - cbind(dist.ran, obs))
  EC[is.nan(EC)] = 1
  ECGD = EC
  ECGD[EC > 1] = GD[EC > 1]
  Cij = (Dmax - obs)/Dmax
  Eij = (Dmax - rand.mean)/Dmax
  Dsij = obs/Dmax
  Gsij = rand.mean/Dmax
  ECijx = Eij/Cij
  CEijx = Cij/Eij
  ECijx[is.nan(ECijx)] = 1
  CEijx[is.nan(CEijx)] = 1
  DGijx = Dsij/Gsij
  GDijx = Gsij/Dsij
  DGijx[is.nan(DGijx)] = 1
  GDijx[is.nan(GDijx)] = 1
  MSTij = (ECijx) * (DGijx)
  MSTij[which(MSTij > 1)] = ((CEijx) * (GDijx))[which(MSTij > 
    1)]

它这里为什么这么写，表示的是什么呢？让我们一步步解析。

在这里，dist.ran指基于原群落距离矩阵而随机形成的系统发育β多样性距离矩阵。

根据代码计算可以得到，计算pNST需要的各个指数的含义

rand.amax：随机矩阵的每一行中的最大值

rand.bmax：对于随机矩阵的每一行，计算密度函数的最大值。这一密度是基于随机化模拟得到的系统发育β多样性值分布。

d.up1：一个判断条件，判断是否需要对rand.bmax进行特殊处理。如果所有观察到的系统发育β多样性距离(obs)和随机化模拟的最大系统发育β多样性距离(rand.amax)都小于或等于1，并且rand.bmax大于1，那么d.up1为TRUE，否则为FALSE。

Dmax：是obs（观察到的最大系统发育β多样性距离）和rand.max（随机化模拟得到的最大系统发育β多样性距离）中的较大值。

GD：随机化模拟的平均系统发育β多样性距离。是一个矩阵，输出的结果包括是随机均值除以所有随机距离矩阵值以及观测值

EC：是一个矩阵，表示观察到的距离与随机化模拟的平均距离的差异，相对于观察到的距离与随机化模拟距离的最大可能差异。

并且，EC中的NaN值得到了等于1的处理。

ECGD：和EC相同的值

ECGD[EC > 1] = GD[EC > 1]：对于EC中大于1的值，使其更换为GD矩阵中对应的值

Cij：是两个样本间实际的系统发育相似性，为观察到的系统发育β多样性距离与最大可能的系统发育β多样性距离的相对偏差。至于为什么这么算，这是因为两样本之间系统发育距离越小代表差异越小，而都与最大值做比较，就相当于把这一值进行了标准化，使得其具有可比性。

Eij：对标Cij的相似性零期望。

Dsij：是实际的系统发育相异性。

Gsij：对标Dsij的相异性零期望。

以上这四个指数，假如为NaN值，都处理为1。

ECijx，CEijx，DGijx，GDijx则分别为以上对应参数的两两比值。

MSTij：为ECijx和DGijx乘积，假如大于1了，那么就用CEijx和GDijx代替。(A、B两种选择情况需要使用不同的公式)

PS：这里的MST其实就是pNST，只不过这一算法是Modified之后的了，所以输出的时候，在表格中显示的名称还是MST。实际上，通过与MST对比可以得到，pNST最后的输出结果，无非就是把比较的距离，从基于分类学β多样性距离替代为基于系统发育的β多样性距离。

实际应用：2024年宁老师5

图4：pNST和地下水最大压力指数(MSI)对数的线性关系

结果表明，pNST随着压力的增大显著降低，表明环境压力的增加给予地下水微生物群落更加强的选择作用。

三、NST代码实操

3.1 tNST(输出结果包含MST)

准备文件：群落文件otu、分组文件group

otu表即为物种表格：行为样本，列为物种

group表格：n×1的data.frame表格

输入数据后，便可以代码分析：

set.seed(123)
tnst <- tNST(comm = otu, group = group, dist.method = 'jaccard', null.model = 'PF', rand = 1000, nworker = 1)

dist.method：相似性度量的方法，推荐用Jaccard，当然可以选择的有很多种。

null.model指零模型方法，默认PF

rand表示随机置换的次数，默认为1000

nworker表示并行线程数，决定着分析的速率。稍微好一点的电脑可以设置为4或者8或者10(亲测可以)

查看数据：

tnst$index.pair  #所有样本对之间的 NST
tnst$index.pair.grp  #仅组内样本对之间的 NST

一般情况下，组内样本对之间的NST更有比较意义。将每个组都看成一个时空群落，不同的组便是不同的群落。这时计算不同组内NST的分布，便可以比较出不同群落之间的随机过程贡献差异。

输出的结果有很多列，但实际上，我们想要的就是最后一列，其表示的是基于分类学相似性度量所算出，且已经过修改的tNST，这个值才是最有效的。

3.2 pNST

otu和group仍然是必须输入的文件，在此基础上，我们还需要输入所有OUT组成的系统发育树，用以读取系统发育距离，从而计算出样本对的系统发育β多样性距离。

tree <- read.tree('tree.nwk')#读取 OTU 的系统发育树文件
tree <- prune.sample(otu, tree) #修剪系统发育树，使其和物种表中的物种对应

set.seed(123)
pnst <- pNST(comm = otu, tree = tree, group = group, phylo.shuffle = TRUE, taxo.null.model = NULL,  
pd.wd = tempdir(), abundance.weighted = TRUE, rand = 1000, nworker = 4, SES = FALSE, RC = FALSE)

phylo.shuffle表示是否要进行系统发育位置置换(默认为TRUE)，SES和RC决定，在输出的表格中是否要输出βNTI和Raup-Crick指数值(一般来说可要可不要，毕竟最后要的一定是pNST)

之后的操作和前面并无差异，也是利用pnst$index.pair和pnst$index.pair.group函数来查看所有组和组内的pNST。

输出的结果有很多列，但实际上，我们想要的就是最后一列，其表示的是基于βMNTD所算出，且已经过修改的pNST，这个值才是最有效的。

四、参考文献

1. Liang, Y. et al. Century long fertilization reduces stochasticity controlling grassland microbial community succession. Soil Biol. Biochem. 151, 108023 (2020).

2. Guo, X. et al. Climate warming leads to divergent succession of grassland microbial communities. Nat. Clim. Change 8, 813–818 (2018).

3. Ning, D. et al. A quantitative framework reveals ecological drivers of grassland microbial community assembly in response to warming. Nat. Commun. 11, 4717 (2020).

4. Stegen, J. C., Lin, X., Konopka, A. E. & Fredrickson, J. K. Stochastic and deterministic assembly processes in subsurface microbial communities. ISME J. 6, 1653–1664 (2012).

5. Ning, D. et al. Environmental stress mediates groundwater microbial community assembly. Nat. Microbiol. 9, 490–501 (2024).