文章目录
- 1. 摘要
- 2. 引言
- 3. 激活函数基础理论
- 4. 经典与常用激活函数详解
- 5. 输出层激活函数专题
- 6. 激活函数的比较与选择指南
- 7. 激活函数的演进、挑战与前沿研究
1. 摘要
激活函数是神经网络架构中不可或缺的核心组件,其首要作用是引入非线性表达能力,从而使网络能够学习和逼近现实世界中复杂的非线性关系。若无激活函数,多层神经网络将退化为简单的线性模型,其表达能力将大打折扣。本报告系统性地回顾了激活函数的定义、核心目的与数学原理,梳理了从经典的Sigmoid、Tanh到广泛应用的ReLU及其变体(如Leaky ReLU, PReLU, ELU, SELU),再到新兴的Swish, GELU, Mish等各类激活函数。针对每种重要的激活函数,报告详细阐述了其数学表达式、图形特征(包括函数本身及其导数)、输出范围、优缺点,并分析了其对网络训练动态(如梯度消失/爆炸、收敛速度、计算效率和稀疏性)的影响。此外,本报告还专门探讨了输出层激活函数(Softmax, Sigmoid, 线性函数)的选择与特定任务类型(分类、回归)的紧密联系。报告进一步提供了激活函数选择的实用指南,并深入探讨了激活函数领域的演进趋势、当前面临的挑战以及未来的研究方向,包括动态激活函数、神经架构搜索发现的激活函数以及注意力机制中的新型激活方式。
2. 引言
2.1 激活函数的定义与重要性
激活函数(Activation Function)是人工神经网络中的一个基础且至关重要的构建单元。在神经元(或节点)中,它接收来自前一层神经元的加权输入信号与偏置项的总和,并对这个总和进行某种(通常是非线性的)变换,产生该神经元的输出信号。这个输出随后作为下一层神经元的输入,或者在输出层直接作为网络的最终预测。
激活函数的核心作用在于向神经网络模型中引入非线性因素。现实世界中的数据和它们之间的关系往往是高度复杂的、非线性的。如果神经网络中没有非线性激活函数,那么无论网络有多少层,每一层的运算都只是对输入进行线性变换(如矩阵乘法和加法)。多个线性变换的组合仍然是一个线性变换,这意味着整个网络本质上等同于一个单层的线性模型。这样的线性模型在处理复杂的、非线性可分的数据(例如图像识别、自然语言理解等任务)时能力非常有限。
通过引入非线性激活函数,神经网络获得了拟合复杂非线性函数的能力,极大地增强了模型的表达能力和灵活性,使其能够学习输入数据中微妙且复杂的模式。这对于深度学习的成功至关重要,因为深度学习模型通常需要通过多层非线性变换来学习数据的高层次抽象特征和表示。因此,激活函数的选择和设计对神经网络的性能、训练动态以及最终能否成功解决特定问题具有深远影响。
3. 激活函数基础理论
3.1 定义与角色
3.1.1 神经元中的激活函数
在人工神经网络的单个神经元模型中,激活函数扮演着"决策者"的角色,决定了该神经元在接收到输入信号后应如何响应以及输出什么。其工作流程通常如下:
加权输入和偏置:神经元接收来自前一层(或输入层)多个神经元的输出信号( x i x_i xi)。每个输入信号都带有一个相应的权重( w i w_i wi),表示该输入对于当前神经元的重要性。此外,还有一个偏置项( b b b)。神经元首先计算这些输入的加权和,并加上偏置项,得到一个净输入值,通常表示为 z z z:
z = ∑ i w i x i + b z = \sum_i w_i x_i + b z=i∑wixi+b
这个 z z z 值是神经元接收到的聚合刺激的线性度量。
激活转换:随后,这个净输入值 z z z 被传递给激活函数 g ( ⋅ ) g(\cdot) g(⋅)。激活函数对 z z z 进行转换,产生神经元的最终输出信号 a a a(也称为激活值):
a = g ( z ) a = g(z) a=g(z)
这个输出 a a a 随后会作为输入传递给网络中的下一层神经元,或者在输出层作为最终的预测结果。
为了更直观地理解激活函数在神经元中的位置和作用,可以设想一个神经元的示意图:
- 输入端:多个输入信号 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn。
- 连接权重:每个输入 x i x_i xi 对应一个权重 w i w_i wi。
- 求和单元:计算加权和 ∑ w i x i \sum w_i x_i ∑wixi,并加上偏置 b b b,得到 z z z。
- 激活单元:将 z z z 输入激活函数 g ( ⋅ ) g(\cdot) g(⋅)。
- 输出端:产生输出 a = g ( z ) a = g(z) a=g(z)。
3.1.2 神经网络中的激活函数
在整个神经网络的宏观层面,激活函数的作用是层层传递并转换信息。网络中的每一层(除了可能的输入层)都由若干个应用了激活函数的神经元组成。前一层的神经元输出(经过激活函数处理)构成了后一层神经元的输入。通过这种方式,激活函数在网络中逐层引入非线性变换。
如果网络中没有激活函数或者只使用线性激活函数(即 g ( z ) = z g(z) = z g(z)=z),那么无论网络有多少层,整个网络的计算最终都可以简化为一个从输入到输出的线性映射。例如,一个两层线性网络可以表示为 y = W 2 ( W 1 x + b 1 ) + b 2 = ( W 2 W 1 ) x + ( W 2 b 1 + b 2 ) = W e f f x + b e f f y = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2) = W_{eff}x + b_{eff} y=W2(W1x+b1)+b2=(W2W1)x+(W2b1+b2)=Weffx+beff,这仍然是一个线性模型。这种线性叠加的特性意味着增加网络的深度并不能增强其表达复杂函数的能力。
而非线性激活函数的引入打破了这种线性局限。每一层非线性激活函数的存在,都使得网络的后续层可以在前一层学习到的特征表示的基础上进行更复杂的非线性组合和抽象。正是这种逐层叠加的非线性变换,赋予了深度神经网络强大的学习和表征能力,使其能够从原始输入数据中学习到高度复杂和抽象的特征,并最终完成如图像分类、语音识别等复杂任务。
3.2 为什么需要激活函数
3.2.1 线性模型的局限性
如前所述,如果一个多层神经网络完全不使用非线性激活函数,或者所有层都仅使用线性激活函数(例如 g ( z ) = c z + d g(z) = cz + d g(z)=cz+d,最简单的是恒等函数 g ( z ) = z g(z) = z g(z)=z),那么整个网络的行为将与一个单层的线性模型等效。这是因为多个线性变换的顺序应用结果仍然是一个线性变换。具体来说,考虑一个没有激活函数的两层网络,其输出可以表示为 y = W 2 ( W 1 x ) y = W_2(W_1x) y=W2(W1x)(为简化,暂时忽略偏置项)。这可以重写为 y = ( W 2 W 1 ) x = W e f f x y = (W_2W_1)x = W_{eff}x y=(W2W1)x=Weffx,其中 W e f f = W 2 W 1 W_{eff} = W_2W_1 Weff=W2W1 是一个新的有效权重矩阵。无论网络有多少这样的线性层,最终都可以被一个等效的单一线性层所取代。
线性模型,如线性回归或逻辑回归(逻辑回归虽然名字带"回归",其核心是线性模型加Sigmoid激活,使其能处理分类),只能学习输入和输出之间的线性关系,或者用线性决策边界来划分数据空间。然而,现实世界中的绝大多数问题,例如图像识别中物体形状的复杂性、自然语言中语义的微妙变化,都涉及到高度非线性的模式和关系。线性模型在这些复杂任务面前往往束手无策,无法捕捉到数据中潜藏的丰富结构,从而导致性能低下。
3.2.2 表达能力的提升
非线性激活函数的引入是神经网络能够超越线性模型局限性的关键。它们赋予了神经网络学习和表示非线性决策边界的能力,从而能够解决线性不可分的问题。一个经典的例子是XOR(异或)问题:给定两个二进制输入,当输入不同时输出1,相同时输出0。这是一个线性不可分问题,单层感知器(不带非线性激活或使用阶跃激活的简单线性模型)无法解决。然而,一个包含非线性激活函数(如ReLU或Sigmoid)的隐藏层的两层神经网络则可以轻松学习并表示XOR函数。
更一般地,通用近似定理(Universal Approximation Theorem)为非线性激活函数的重要性提供了坚实的理论基础。该定理指出,一个具有至少一个包含"挤压"性质(squashing property,如Sigmoid或Tanh,或者更广义的非多项式)的非线性激活函数的隐藏层,并且该隐藏层拥有足够数量的神经元的前馈神经网络,可以以任意精度逼近定义在输入空间紧集上的任何连续函数。这意味着,理论上,这样的神经网络具有强大的表达能力,能够模拟各种复杂的输入输出映射关系。虽然定理本身没有说明如何找到合适的权重或需要多少神经元,但它强调了非线性激活函数对于实现这种通用近似能力的核心作用。没有非线性,这种强大的表达能力将不复存在。
3.3 理想激活函数的特性
在设计和选择激活函数时,研究者们通常会考虑一系列理想的特性,这些特性有助于提升神经网络的训练效率、稳定性和最终性能。
3.3.1 非线性 (Non-linearity)
这是激活函数最基本也是最重要的特性。如前所述,非线性使得多层网络能够学习复杂模式,否则网络将退化为线性模型。
3.3.2 可微性 (Differentiability)
激活函数应该在其定义域的大部分区域(尤其是神经元活跃的区域)是可微的。这是因为目前主流的神经网络训练算法,如反向传播(Backpropagation),依赖于梯度信息来更新网络权重。如果激活函数不可微或在很多点导数为零,梯度计算将受阻,网络可能无法有效学习。即使像ReLU这样在原点不可微的函数,在实践中也可以通过定义次梯度或在不可微点赋予一个特定的梯度值(如0或1)来处理。
3.3.3 单调性 (Monotonicity)
单调的激活函数(即其输出随着输入的增加而单向增加或单向减少)曾被认为是一个理想特性,因为它可以保证对于单层网络,损失函数是凸的,从而简化优化过程。然而,现代深度学习的研究表明,一些表现优异的新型激活函数,如Swish和Mish,是非单调的。这表明非单调性可能允许网络学习更复杂的函数,或者对梯度流有更精细的控制,从而在某些情况下带来性能提升。因此,单调性不再被视为一个绝对的理想标准,而是需要根据具体情况权衡。
3.3.4 输出范围 (Output Range)
激活函数的输出范围对其行为和网络训练有显著影响。
有界 vs. 无界 (Bounded vs. Unbounded):
- 有界输出(如Sigmoid的 ( 0 , 1 ) (0,1) (0,1)范围或Tanh的 ( − 1 , 1 ) (-1,1) (−1,1)范围)可以将激活值限制在一个固定的区间内。这有助于稳定学习过程,特别是在网络的早期阶段,可以防止激活值因权重更新而变得过大,从而可能导致更稳定的梯度传播。
- 无界输出(如ReLU的 [ 0 , ∞ ) [0,\infty) [0,∞)范围)则允许激活值取任意大的正值。这可能有助于网络更快地学习,因为它们不会限制信号的强度。然而,无界激活也可能增加梯度爆炸或激活值本身爆炸的风险,需要更谨慎的权重初始化和学习率设置。
零中心化 (Zero-centered):
如果激活函数的输出大致以0为中心(例如Tanh的输出范围是
(
−
1
,
1
)
(-1,1)
(−1,1),ELU的输出在负区也可以取负值),这通常被认为是一个有利的特性。如果激活函数的输出始终为正(如Sigmoid的
(
0
,
1
)
(0,1)
(0,1)或ReLU的
[
0
,
∞
)
[0,\infty)
[0,∞)),那么在反向传播过程中,传递到前一层权重的梯度将具有相同的符号(都为正或都为负,取决于损失函数对当前层输出的梯度符号)。这会导致权重更新在参数空间中呈现"之"字形(zig-zagging)的路径,从而降低优化效率和收敛速度。零中心化的输出则可以缓解这个问题,使得梯度更新方向更加多样化和高效。
3.3.5 梯度特性 (Gradient Characteristics)
激活函数的导数特性直接影响梯度在网络中的传播,是决定网络能否成功训练的关键。
避免梯度饱和 (Avoiding Saturation):
饱和是指当输入值非常大或非常小时,激活函数的导数(梯度)趋近于零的现象。Sigmoid和Tanh函数在其输入的两端都会饱和。当神经元工作在饱和区时,其梯度非常小,这会导致通过该神经元的梯度在反向传播时几乎消失,使得连接到该神经元的权重几乎不被更新。在深层网络中,如果许多神经元都饱和,梯度信号逐层衰减,最终可能导致网络前端的层完全停止学习,这就是所谓的梯度消失问题 (Vanishing Gradient Problem)。因此,理想的激活函数应尽可能避免或减轻饱和现象,尤其是在其常用的激活区域。
梯度不消失/不爆炸 (Non-vanishing/exploding gradients):
除了饱和导致的梯度消失,激活函数的选择也应有助于维持梯度的"健康"幅度,使其既不会在深层网络中变得过小(梯度消失),也不会变得过大(梯度爆炸 (Exploding Gradient Problem))。梯度爆炸会导致权重更新过大,使得学习过程不稳定甚至发散。虽然梯度爆炸问题通常可以通过梯度裁剪等技术来缓解,但激活函数本身的特性也应有助于梯度的稳定传播。例如,ReLU及其变体由于在正区梯度恒为1,很大程度上缓解了梯度消失问题。
3.3.6 计算效率 (Computational Efficiency)
激活函数及其导数的计算应该尽可能简单和快速。在神经网络的训练(前向传播和反向传播)和推理(前向传播)过程中,激活函数会在每个神经元上被调用,因此其计算成本对整体的训练和推理速度有直接影响。例如,ReLU函数 f ( x ) = max ( 0 , x ) f(x) = \max(0,x) f(x)=max(0,x) 及其导数的计算非常简单,相比之下,Sigmoid和Tanh函数由于涉及到指数运算,计算成本相对较高。
3.3.7 稀疏性诱导 (Sparsity Inducement)
某些激活函数(最典型的是ReLU)能够使一部分神经元的输出为零。这种特性被称为稀疏激活。稀疏性可能带来一些好处:
- 信息解耦与特征选择:不同的神经元可能对输入的不同特征做出响应,稀疏激活有助于形成更具区分性和更少冗余的特征表示。
- 计算效率:如果大量神经元的输出为零,那么在后续的计算中可以跳过这些神经元,从而节省计算资源(尽管这在硬件和软件实现上需要特定支持)。
- 减少过拟合:稀疏性在一定程度上可以起到正则化的作用,减少模型参数间的依赖,可能有助于提高模型的泛化能力。
这些理想特性之间往往存在权衡。例如,计算简单的ReLU解决了Sigmoid/Tanh的梯度饱和问题,但引入了"Dying ReLU"问题和非零中心输出问题。因此,激活函数的选择通常需要根据具体任务、网络架构和经验进行综合考虑。激活函数的设计和研究本身就是一个持续演进的过程,旨在更好地平衡这些特性以达到更优的网络性能。例如,早期的理想特性如严格的单调性,在Swish和Mish等非单调函数展现出优越性能后,其重要性受到了重新评估。这表明,我们对"理想"激活函数的理解,是随着深度学习理论和实践的发展而不断深化的。
4. 经典与常用激活函数详解
本章节将详细介绍一系列在深度学习发展历程中具有重要地位以及当前仍被广泛使用的激活函数。对于每个函数,我们将提供其数学表达式、函数本身及其导数的图形特征描述、输出值域、主要优缺点(特别是对梯度传播、计算效率和网络稀疏性的影响),以及典型的应用场景和在主流深度学习框架中的实现方式。
4.1 Sigmoid 函数
Sigmoid函数,也常被称为逻辑斯谛函数(Logistic function),是最早被广泛使用的激活函数之一。
数学表达式:
f
(
x
)
=
σ
(
x
)
=
1
1
+
e
−
x
f(x) = \sigma(x) = \frac{1}{1 + e^{-x}}
f(x)=σ(x)=1+e−x1
函数图形及其导数图形:
-
函数图形: Sigmoid函数的图形呈现出典型的"S"型曲线。它是一个平滑、连续且单调递增的函数。当输入 x x x 趋向于负无穷大时,函数值趋近于0;当 x x x 趋向于正无穷大时,函数值趋近于1;当 x = 0 x=0 x=0 时,函数值为0.5。

-
导数图形: Sigmoid函数的导数可以用其自身表示: f ′ ( x ) = σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) f'(x) = \sigma'(x) = \sigma(x)(1-\sigma(x)) f′(x)=σ′(x)=σ(x)(1−σ(x))。其导数图形是一条钟形曲线(类似高斯分布的形状,但不完全相同),在 x = 0 x=0 x=0 处达到最大值0.25。当输入 x x x 的绝对值增大时,导数值迅速减小并趋近于0。

输出值域: ( 0 , 1 ) (0,1) (0,1)
优点:
- 输出有界且可解释为概率: Sigmoid函数的输出值被限制在 ( 0 , 1 ) (0,1) (0,1)之间,这使得其输出可以被自然地解释为概率,例如在二分类任务中表示样本属于某个类别的概率。
- 平滑且处处可微: 函数本身是平滑的,并且在其整个定义域内都是可微的,这对于基于梯度的优化算法(如反向传播)是必需的。
缺点:
- 梯度消失 (Vanishing Gradient): 这是Sigmoid函数最主要的问题。当输入值非常大( x ≫ 0 x \gg 0 x≫0)或非常小( x ≪ 0 x \ll 0 x≪0)时,Sigmoid函数会进入饱和区,其导数值非常接近于0。在深度神经网络中,这些小梯度在反向传播过程中会逐层相乘,导致梯度信号迅速衰减,使得网络深处的层接收到的梯度信号过小,权重更新缓慢甚至停滞,从而难以有效训练深层网络。
- 输出非零中心 (Output Not Zero-Centered): Sigmoid函数的输出值恒为正(在 ( 0 , 1 ) (0,1) (0,1)区间内),其均值不为0。如果一个神经元的输入总是正的(例如前一层激活函数的输出都是正的),那么反向传播时计算得到的对权重的梯度将都具有相同的符号(要么全为正,要么全为负,具体取决于损失函数对该神经元输出的梯度符号)。这会导致权重更新在参数空间中以"之"字形(zig-zagging)的方式进行,降低了优化效率和收敛速度。
- 计算成本相对较高 (Relatively High Computational Cost): Sigmoid函数包含指数运算 ( e − x ) (e^{-x}) (e−x),相对于简单的线性或分段线性函数(如ReLU),其计算成本更高。
典型应用场景:
- 隐藏层: 在早期神经网络中,Sigmoid曾被广泛用作隐藏层的激活函数。然而,由于上述梯度消失和非零中心问题,它在现代深度网络隐藏层中的应用已基本被ReLU及其变体所取代。斯坦福大学的CS231n课程甚至建议"不要使用Sigmoid"作为隐藏层激活。
- 输出层:
- 二分类问题: Sigmoid函数是二分类问题输出层最常用的激活函数,输出单个概率值。
- 多标签分类问题: 在多标签分类任务中(一个样本可以同时属于多个类别),输出层的每个神经元(对应一个标签)可以使用Sigmoid函数独立地输出该标签存在的概率。
- 特定网络结构: 在一些循环神经网络(RNNs)的门控单元中,如长短期记忆网络(LSTM)和门控循环单元(GRU)中的各种门(例如遗忘门、输入门、输出门),Sigmoid函数仍被用来控制信息的流动,因为其 ( 0 , 1 ) (0,1) (0,1)的输出范围适合表示门的开闭程度。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.sigmoid(input)或torch.nn.Sigmoid() - TensorFlow/Keras:
tf.keras.activations.sigmoid(x)或在层定义中指定activation='sigmoid'
4.2 Tanh 函数 (Hyperbolic Tangent Function)
Tanh函数,即双曲正切函数,是Sigmoid函数的另一个早期替代品,它在某些方面表现出优于Sigmoid的特性。
数学表达式:
f
(
x
)
=
tanh
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
=
2
⋅
σ
(
2
x
)
−
1
f(x) = \tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} = 2 \cdot \sigma(2x) - 1
f(x)=tanh(x)=ex+e−xex−e−x=2⋅σ(2x)−1
从第二个等式可以看出,Tanh函数本质上是Sigmoid函数的一个缩放和平移版本。
函数图形及其导数图形:
-
函数图形: Tanh函数的图形也是"S"型的,与Sigmoid函数形状相似。但其输出范围是 ( − 1 , 1 ) (-1, 1) (−1,1),并且函数图像关于原点对称(即 f ( − x ) = − f ( x ) f(-x) = -f(x) f(−x)=−f(x))。

-
导数图形: Tanh函数的导数为 f ′ ( x ) = 1 − tanh 2 ( x ) f'(x) = 1 - \tanh^2(x) f′(x)=1−tanh2(x)。其导数图形也是钟形的,在 x = 0 x=0 x=0 处达到最大值1。与Sigmoid的导数(最大值为0.25)相比,Tanh在原点附近的梯度更陡峭。
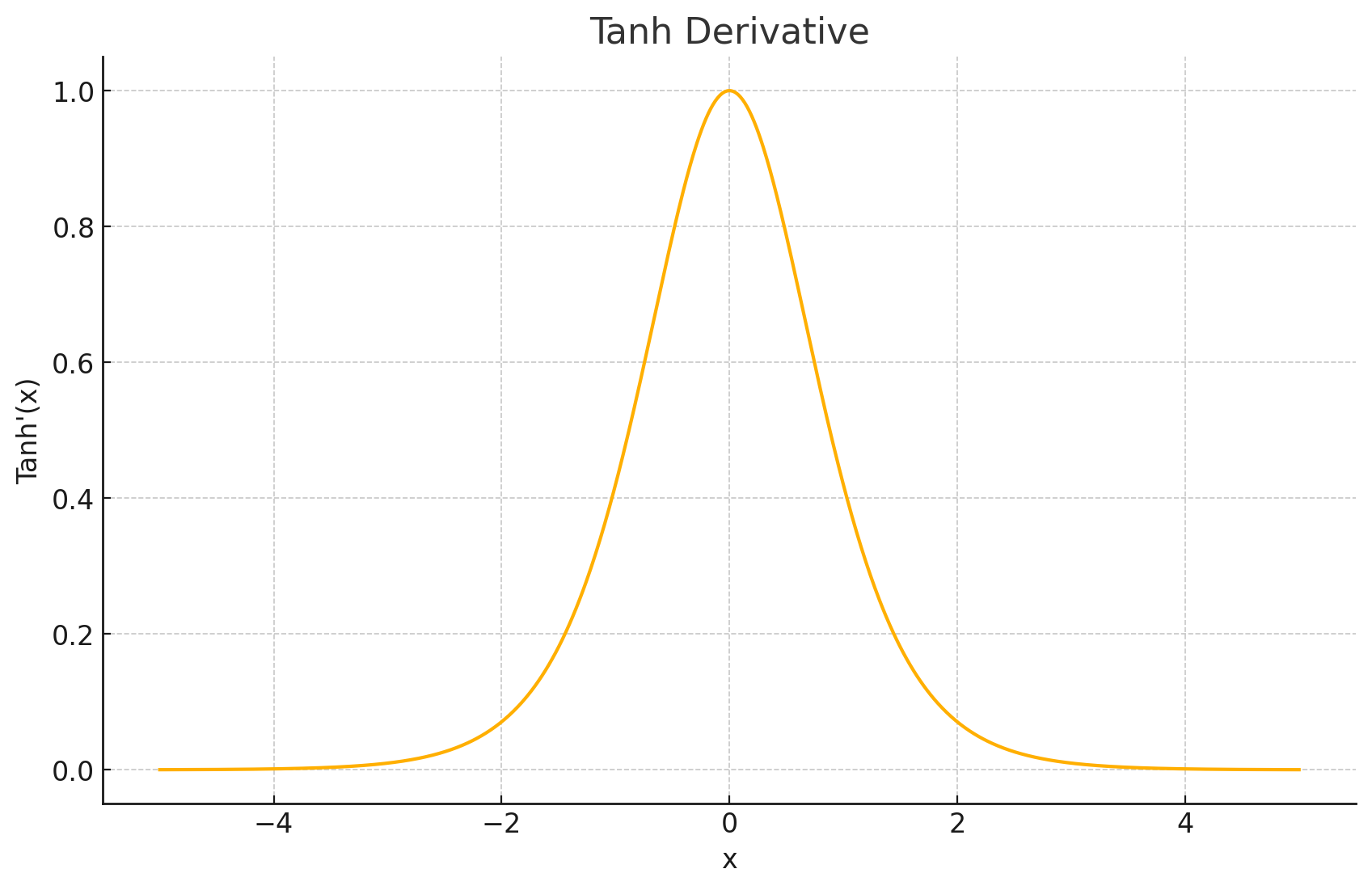
输出值域: ( − 1 , 1 ) (-1,1) (−1,1)
优点:
- 输出零中心化 (Zero-centered Output): Tanh函数的输出范围是 ( − 1 , 1 ) (-1, 1) (−1,1),其均值接近于0。这被认为是Tanh相对于Sigmoid的一个主要优势,因为零中心化的输出可以使得下一层神经元的输入也近似零中心,从而有助于梯度在反向传播过程中更有效地更新权重,避免Sigmoid非零中心输出可能导致的"之"字形优化路径,通常能带来更快的收敛速度。
- 梯度比Sigmoid更强 (Stronger Gradient than Sigmoid): Tanh函数在原点附近的导数(梯度)为1,而Sigmoid在原点附近的导数为0.25。这意味着在激活值接近0的区域,Tanh能提供更大的梯度信号,这在一定程度上有助于缓解梯度消失问题,尤其是在较浅的网络中。
缺点:
- 梯度消失 (Vanishing Gradient): 尽管Tanh在零点附近的梯度比Sigmoid强,但它仍然是一个饱和函数。当输入值的绝对值较大时,Tanh函数也会饱和(输出趋近于-1或1),其导数同样会趋近于0,从而导致梯度消失问题,尤其是在深层网络中。
- 计算成本相对较高 (Relatively High Computational Cost): 与Sigmoid类似,Tanh函数也包含指数运算,因此计算成本高于ReLU等非饱和激活函数。
典型应用场景:
- 隐藏层激活: 在ReLU及其变体出现之前,Tanh因其零中心化的特性,通常被认为是优于Sigmoid的隐藏层激活函数选择。如果数据已经被归一化到零均值,使用Tanh可能效果更好。
- 循环神经网络 (RNNs): Tanh在传统的RNN以及LSTM、GRU等门控RNN的隐藏状态更新中非常常见,因其有界的输出范围有助于控制循环动态的稳定性。
尽管Tanh优于Sigmoid,但在许多现代深度学习应用中,尤其是在卷积神经网络(CNNs)和深层前馈网络中,其隐藏层激活的角色也多被ReLU及其变体取代。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.tanh(input)或torch.nn.Tanh() - TensorFlow/Keras:
tf.keras.activations.tanh(x)或在层定义中指定activation='tanh'
4.3 ReLU 函数 (Rectified Linear Unit)
ReLU(Rectified Linear Unit,修正线性单元)是近年来深度学习领域最受欢迎和广泛应用的激活函数之一,它的出现显著推动了深度神经网络的发展。
数学表达式:
f
(
x
)
=
max
(
0
,
x
)
f(x) = \max(0,x)
f(x)=max(0,x)
也可以表示为分段函数形式:
f
(
x
)
=
{
x
if
x
>
0
0
if
x
≤
0
f(x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}
f(x)={x0if x>0if x≤0
函数图形及其导数图形:
-
函数图形: ReLU函数的图形非常简洁:当输入 x x x 为负数或零时,输出为0;当输入 x x x 为正数时,输出等于输入 x x x 本身。这形成了一个在原点处有拐角的折线,原点左侧是平坦的直线( y = 0 y=0 y=0),右侧是斜率为1的直线( y = x y=x y=x)。

-
导数图形: ReLU函数的导数也同样简单:当 x < 0 x<0 x<0 时,导数为0;当 x > 0 x>0 x>0 时,导数为1。在 x = 0 x=0 x=0 点,ReLU函数是不可导的,但在实践中,通常将其在该点的次梯度定义为0或1。

输出值域: [ 0 , ∞ ) [0,\infty) [0,∞)
优点:
- 计算高效 (Computationally Efficient): ReLU及其导数的计算都非常简单,只涉及比较和基本的算术运算,远快于Sigmoid和Tanh函数中的指数运算,这使得包含大量ReLU单元的深层网络训练和推理速度更快。
- 缓解梯度消失 (Alleviates Vanishing Gradient): 对于所有正输入,ReLU的梯度恒为1。这意味着在反向传播过程中,只要神经元的输入为正,梯度就可以无衰减地向前传播,有效缓解了Sigmoid和Tanh等饱和函数在深层网络中容易引发的梯度消失问题,使得训练非常深的网络成为可能。
- 引入稀疏性 (Induces Sparsity): ReLU会将所有负输入置为0,这意味着在任何给定时间,网络中只有一部分神经元是"激活"的(输出非零值)。这种稀疏激活的特性被认为有助于形成更解耦、更鲁棒的特征表示,可能减少参数间的依赖,起到一定的正则化作用,并可能提高计算效率(尽管后者依赖于特定的软硬件实现)。
- 加速收敛 (Faster Convergence): 实践表明,使用ReLU激活函数的神经网络通常比使用Sigmoid或Tanh的同类网络收敛速度快得多,有时甚至快数倍。
缺点:
- 输出非零中心 (Output Not Zero-Centered): ReLU的输出值总是非负的( ≥ 0 \geq 0 ≥0),与Sigmoid类似,其输出不是以0为中心的。这可能导致与Sigmoid类似的梯度更新效率问题。
- Dying ReLU 问题 (Dying ReLU Problem): 这是ReLU最显著的缺点。如果在训练过程中,一个ReLU神经元的权重被更新,导致其对于所有训练样本的输入都变为负数,那么该神经元的输出将恒为0。由于当输入为负时ReLU的梯度也为0,这个神经元在后续的反向传播中将不再接收任何梯度信号,其权重也无法再得到更新。这个神经元就"死亡"了,不再对网络的学习做出贡献。较大的学习率或不当的权重初始化可能会加剧此问题。
- 激活值无上界 (Unbounded Activation): ReLU的输出在正区间是无界的,这意味着激活值可能会变得非常大。虽然这有助于避免梯度饱和,但也可能在某些情况下导致梯度爆炸或数值不稳定的问题,需要配合适当的权重正则化或梯度裁剪技术。
典型应用场景:
- ReLU是目前深度神经网络(尤其是卷积神经网络CNNs和许多类型的前馈网络)中隐藏层的默认和首选激活函数。
- 不建议在循环神经网络(RNNs)的循环连接中使用ReLU,因为它可能导致激活值无界累积。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.relu(input)或torch.nn.ReLU() - TensorFlow/Keras:
tf.keras.activations.relu(x)或在层定义中指定activation='relu'
ReLU的成功及其"Dying ReLU"等固有缺陷,催生了一系列旨在改进其性能的变体激活函数。这些变体通常试图在保留ReLU主要优点的同时,解决其存在的问题。
4.4 ReLU 变体 (ReLU Variants)
针对标准ReLU函数存在的问题,尤其是"Dying ReLU"现象,研究者们提出了一系列的改进版本。这些变体旨在通过修改ReLU在负输入区的行为来提升性能和训练稳定性。
4.4.1 Leaky ReLU (LReLU)
Leaky ReLU是对标准ReLU的一个简单而有效的改进,旨在解决神经元"死亡"的问题。
数学表达式:
f
(
x
)
=
{
x
if
x
>
0
α
x
if
x
≤
0
f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}
f(x)={xαxif x>0if x≤0
其中, α \alpha α 是一个小的正常数(超参数),通常取值为0.01或类似的小值。
函数图形及其导数图形:
-
函数图形: Leaky ReLU的图形与ReLU非常相似。在输入 x > 0 x>0 x>0 时,它是一条斜率为1的直线 ( y = x ) (y=x) (y=x)。不同之处在于当输入 x ≤ 0 x \leq 0 x≤0 时,它不再是输出恒为0的平线,而是一条斜率为 α \alpha α 的直线 ( y = α x ) (y=\alpha x) (y=αx)。由于 α \alpha α 通常很小,这条线的斜率非常平缓,但非零。

-
导数图形: Leaky ReLU的导数是一个分段常数函数:当 x > 0 x>0 x>0 时,导数为1;当 x < 0 x<0 x<0 时,导数为 α \alpha α。在 x = 0 x=0 x=0 点不可导,实践中通常按需处理。

输出值域: ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)
优点:
- 解决Dying ReLU问题: 通过在负输入区引入一个小的非零梯度 ( α ) (\alpha) (α),Leaky ReLU允许负值输入时神经元仍然可以进行权重更新,从而防止神经元完全"死亡"。
- 计算依然高效: 计算复杂度与ReLU基本持平,仍然非常高效。
缺点:
- α \alpha α 的选择: 参数 α \alpha α 的值通常需要手动设置(如0.01),其最优值可能因任务和数据集而异,选择不当可能影响性能。
- 性能提升不一致: 一些研究表明,Leaky ReLU相对于标准ReLU的性能提升并不总是一致或非常显著的。其效果可能依赖于具体的应用场景。
典型应用场景:
- 作为标准ReLU的一个替代方案,特别是在怀疑网络中存在大量"死亡"神经元并影响模型性能时。
- 在一些生成对抗网络(GANs)中也有应用。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.LeakyReLU(negative_slope=0.01) - TensorFlow/Keras:
tf.keras.layers.LeakyReLU(alpha=0.01)或通过tf.keras.activations.relu设置negative_slope参数。
4.4.2 Parametric ReLU (PReLU)
Parametric ReLU (PReLU) 是Leaky ReLU的一个扩展,它将负区间的斜率 α \alpha α 作为一个可学习的参数,而不是固定的超参数。
数学表达式:
f
(
x
i
)
=
{
x
i
if
x
i
>
0
a
i
x
i
if
x
i
≤
0
f(x_i) = \begin{cases} x_i & \text{if } x_i > 0 \\ a_i x_i & \text{if } x_i \leq 0 \end{cases}
f(xi)={xiaixiif xi>0if xi≤0
其中, a i a_i ai 是一个可学习的参数。这个参数可以是对所有通道共享的(channel-shared),也可以是每个通道独有的(channel-wise)。
函数图形及其导数图形:
-
函数图形: PReLU的图形与Leaky ReLU类似,都是在原点处有拐点的折线。不同之处在于,其负输入区间的斜率 a i a_i ai 是通过反向传播从数据中学习得到的,而不是预先设定的。

-
导数图形: 当 x i > 0 x_i>0 xi>0 时,导数为1;当 x i < 0 x_i<0 xi<0 时,导数为学习到的参数 a i a_i ai。
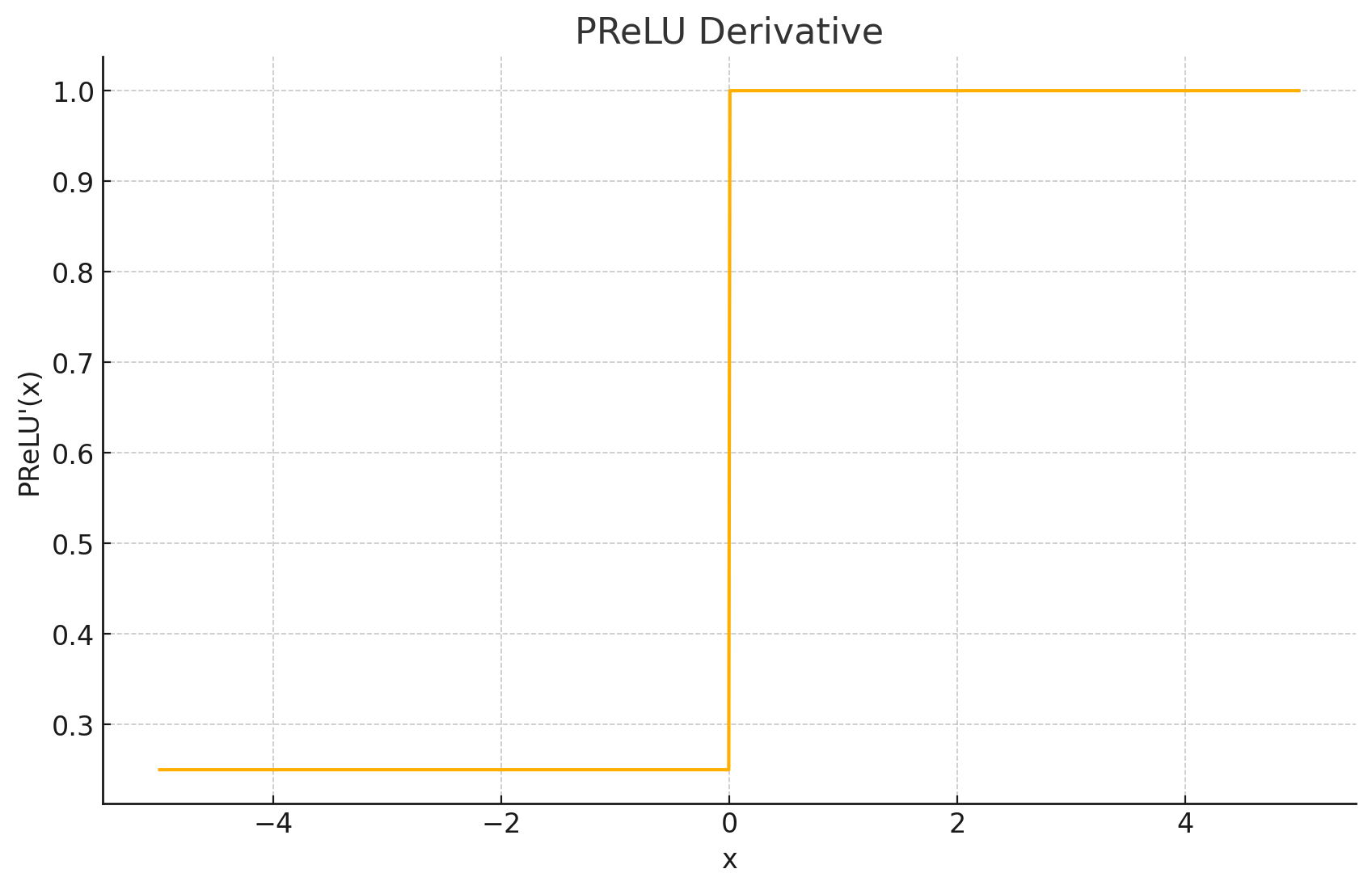
输出值域: ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)
优点:
- 自适应学习负斜率: PReLU允许网络根据数据自动学习最合适的负区间斜率,这使得它比Leaky ReLU具有更大的灵活性,并可能在多种任务上获得比ReLU和Leaky ReLU更好的性能。
- 解决Dying ReLU问题: 与Leaky ReLU一样,通过允许负值输入时存在非零梯度,PReLU也有效地解决了Dying ReLU问题。
缺点:
- 增加模型参数: 引入了额外的可学习参数 a i a_i ai,这会略微增加模型的复杂度和参数量。在数据量较小的情况下,可能会增加过拟合的风险。
- 训练复杂度略增: 参数的学习过程会给训练带来额外的计算开销,尽管通常不大。
典型应用场景:
- 当标准ReLU或Leaky ReLU表现不佳时,PReLU可以作为一种更具适应性的替代方案,尤其是在有足够数据支持参数学习的情况下。
- 在一些大规模图像识别任务中取得了成功。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.PReLU(num_parameters=1, init=0.25)(num_parameters可以设为1或通道数) - TensorFlow/Keras:
tf.keras.layers.PReLU(alpha_initializer='zeros', shared_axes=None)
4.4.3 Exponential Linear Unit (ELU)
Exponential Linear Unit (ELU) 是另一种旨在解决ReLU问题的激活函数,它在负值区域引入了指数衰减。
数学表达式:
f
(
x
)
=
{
x
if
x
>
0
α
(
e
x
−
1
)
if
x
≤
0
f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x-1) & \text{if } x \leq 0 \end{cases}
f(x)={xα(ex−1)if x>0if x≤0
其中, α \alpha α 是一个大于0的超参数,控制着ELU在负值区的饱和水平,通常默认设为1.0。
函数图形及其导数图形:
-
函数图形: ELU在正输入区与ReLU相同,为一条斜率为1的直线 ( y = x ) (y=x) (y=x)。在负输入区,它是一条平滑的指数曲线,随着 x x x 趋向负无穷,函数值趋向于 − α -\alpha −α。

-
导数图形: 当 x > 0 x>0 x>0 时,导数为1。当 x < 0 x<0 x<0 时,导数为 α e x \alpha e^x αex。另一种等价的表达是,当 x ≤ 0 x \leq 0 x≤0 时,导数为 f ( x ) + α f(x)+\alpha f(x)+α。在 x = 0 x=0 x=0 处,导数从左逼近 α \alpha α,从右逼近1,因此在0点不可导(除非 α = 1 \alpha=1 α=1)。

输出值域: ( − α , ∞ ) (-\alpha,\infty) (−α,∞)
优点:
- 缓解Dying ReLU问题: 允许负值输入时存在非零梯度。
- 输出更接近零中心: ELU的负值部分可以输出负值,这有助于将神经元激活的均值推向0,从而可能加速学习过程,类似于Tanh的优点。
- 对噪声具有一定的鲁棒性: ELU在负值区域的饱和特性(趋向于 − α -\alpha −α)可能使网络对输入噪声不那么敏感。
- 平滑的负值激活: 与Leaky ReLU和PReLU在原点的尖锐拐角不同,ELU在整个定义域内(除原点外,若 α = 1 \alpha=1 α=1)是平滑的(C1连续,如果 α = 1 \alpha=1 α=1则在原点也C1连续),这可能有助于优化。
缺点:
- 计算复杂度较高: 负值部分包含指数运算 ( e x ) (e^x) (ex),因此计算成本高于ReLU、Leaky ReLU和PReLU。
- α \alpha α 参数选择: 需要选择超参数 α \alpha α。
典型应用场景:
- 作为ReLU及其线性变体的一个替代品,尤其是在希望获得更平滑激活、零中心化输出或更好噪声鲁棒性的场景中。
- 在一些计算机视觉任务中表现良好。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.ELU(alpha=1.0, inplace=False) - TensorFlow/Keras:
tf.keras.activations.elu(x, alpha=1.0)或在层定义中指定activation='elu'
4.4.4 Scaled Exponential Linear Unit (SELU)
Scaled Exponential Linear Unit (SELU) 是ELU的一个特殊变体,其设计目标是实现网络的自归一化(self-normalizing)。
数学表达式:
f
(
x
)
=
λ
{
x
if
x
>
0
α
(
e
x
−
1
)
if
x
≤
0
f(x) = \lambda \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x-1) & \text{if } x \leq 0 \end{cases}
f(x)=λ{xα(ex−1)if x>0if x≤0
其中, λ \lambda λ (scale) 和 α \alpha α 是两个特定的常数,其值是根据数学推导得出的,以确保自归一化特性。通常 λ ≈ 1.050700987 \lambda \approx 1.050700987 λ≈1.050700987 且 α ≈ 1.673263242 \alpha \approx 1.673263242 α≈1.673263242。
函数图形及其导数图形:
-
函数图形: SELU的图形形状与ELU非常相似,但在整体上进行了缩放(乘以 λ \lambda λ)。正输入区是斜率为 λ \lambda λ 的直线,负输入区是指数衰减并趋向于 − λ α -\lambda\alpha −λα。

-
导数图形: SELU的导数也是ELU导数的一个缩放版本。当 x > 0 x>0 x>0 时,导数为 λ \lambda λ。当 x < 0 x<0 x<0 时,导数为 λ α e x \lambda\alpha e^x λαex (或 f ( x ) / λ + λ α f(x)/\lambda+\lambda\alpha f(x)/λ+λα 的变体)。

输出值域: ( − λ α , ∞ ) (-\lambda\alpha,\infty) (−λα,∞)
优点:
- 自归一化 (Self-Normalizing): 这是SELU最核心的特性。在满足特定条件(例如,权重使用Lecun正态分布初始化,网络层是全连接的,并且使用AlphaDropout进行正则化)的情况下,SELU可以使得神经元的激活值在网络传播过程中自动收敛到零均值和单位方差。这有助于防止梯度消失和梯度爆炸问题,使得训练非常深的网络成为可能,且通常不需要使用批归一化(Batch Normalization)。
缺点:
- 对网络架构和初始化有严格要求: SELU的自归一化特性依赖于特定的网络结构(主要是堆叠的全连接层)、权重初始化方案(Lecun Normal)和特定的Dropout变体(AlphaDropout)。如果这些条件不满足,自归一化效果可能无法保证。
- 计算复杂度较高: 与ELU类似,包含指数运算,计算成本高于ReLU。
- 在CNN等结构中效果不明确: SELU最初主要针对全连接网络设计和验证,其在卷积神经网络等其他常见结构中的普适性和优势尚不如ReLU及其简单变体那样明确。
典型应用场景:
- 主要用于需要训练非常深的全连接神经网络(Feedforward Neural Networks, FNNs 或 Multi-Layer Perceptrons, MLPs),并且希望避免使用批归一化层的情况。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.SELU(inplace=False) - TensorFlow/Keras:
tf.keras.activations.selu(x)或在层定义中指定activation='selu'
ReLU及其变体的出现,标志着激活函数研究的一个重要转折点,它们极大地推动了深度学习模型向更深层次发展。然而,研究者们并未停止探索,后续又涌现出如Swish、GELU、Mish等更复杂的函数,试图在性能和特性上取得进一步的突破。
4.5 Swish 函数 (Swish Function / SiLU)
Swish函数,也被称为SiLU (Sigmoid-weighted Linear Unit) 当其参数 β = 1 \beta=1 β=1 时,是由Google的研究人员通过神经架构搜索(NAS)发现的一种新型激活函数。它因其简单性以及在多种具有挑战性的数据集和深度模型上优于ReLU的表现而受到关注。
数学表达式:
f
(
x
)
=
x
⋅
σ
(
β
x
)
=
x
1
+
e
−
β
x
f(x) = x \cdot \sigma(\beta x) = \frac{x}{1+e^{-\beta x}}
f(x)=x⋅σ(βx)=1+e−βxx
其中, σ ( ⋅ ) \sigma(\cdot) σ(⋅) 是Sigmoid函数, β \beta β 是一个常数或可学习的参数。当 β = 1 \beta=1 β=1 时,Swish等同于SiLU。
函数图形及其导数图形:
-
函数图形: Swish函数是一条平滑的、非单调的曲线。与ReLU不同,它在负值区域允许出现负输出,并在接近零的负值区域有一个小的下凹(dip),然后随着输入趋向负无穷而趋近于一个小的负常数(当 β = 1 \beta=1 β=1时约为-0.278)。在正值区域,它近似线性增长,但比ReLU增长略慢。

-
导数图形: Swish函数的导数较为复杂,其形式为 f ′ ( x ) = σ ( β x ) + β x σ ( β x ) ( 1 − σ ( β x ) ) f'(x) = \sigma(\beta x) + \beta x \sigma(\beta x)(1-\sigma(\beta x)) f′(x)=σ(βx)+βxσ(βx)(1−σ(βx)),可以简化为 f ′ ( x ) = swish ( x ) / β + σ ( β x ) ( 1 − swish ( x ) / β ) f'(x) = \text{swish}(x)/\beta + \sigma(\beta x)(1-\text{swish}(x)/\beta) f′(x)=swish(x)/β+σ(βx)(1−swish(x)/β)。另一种常见的形式(当 β = 1 \beta=1 β=1)是 f ′ ( x ) = f ( x ) + σ ( x ) ( 1 − f ( x ) ) f'(x) = f(x) + \sigma(x)(1-f(x)) f′(x)=f(x)+σ(x)(1−f(x))。其导数图形也是非单调的,并且在某些区域可以大于1。

输出值域: 当 β = 1 \beta=1 β=1 时,近似为 ( ≈ − 0.278 , ∞ ) (\approx-0.278,\infty) (≈−0.278,∞)。通常是下有界,上无界。
优点:
- 平滑且非单调 (Smooth and Non-monotonic): Swish的平滑性使其在优化过程中表现良好,而非单调性(即函数值并非随输入单向变化)被认为是其能够学习更复杂模式并超越ReLU等单调函数的原因之一。
- 自门控机制 (Self-gating): Swish函数的形式 x ⋅ σ ( β x ) x \cdot \sigma(\beta x) x⋅σ(βx) 可以看作是一种自门控机制,其中输入 x x x 本身通过Sigmoid函数 σ ( β x ) \sigma(\beta x) σ(βx)(作为门)来调节其自身的传播。
- 性能优越: 在许多深度学习模型和基准测试中(尤其是在较深的网络中),Swish的表现通常优于ReLU及其一些变体。例如,在ImageNet分类任务上,用Swish替换ReLU可以带来显著的准确率提升。
- 无上界避免饱和,有下界助于正则化: 正值区域无上界,避免了类似Sigmoid/Tanh的饱和问题;负值区域有下界,可能有助于正则化。
缺点:
- 计算成本高于ReLU: 由于包含了Sigmoid函数的计算(指数运算),Swish的计算成本比ReLU更高。这在训练大规模模型时可能会成为一个考虑因素。
典型应用场景:
- 作为ReLU在各种深度神经网络中的高性能替代品,特别是在计算机视觉(如EfficientNets)和自然语言处理等领域的复杂模型中。
- 当计算资源允许,并且追求极致性能时,可以尝试使用Swish。
PyTorch/TensorFlow 实现:
- PyTorch: 从PyTorch 1.7版本开始,内置了
torch.nn.SiLU()(SiLU是Swish在 β = 1 \beta=1 β=1 时的名称)。 - TensorFlow/Keras:
tf.keras.activations.swish(x)或在层定义中指定activation='swish'。
4.6 GELU 函数 (Gaussian Error Linear Unit)
GELU (Gaussian Error Linear Unit) 是另一种现代激活函数,因其在Transformer等先进模型中的成功应用而广为人知。它的设计思想是结合ReLU的线性特性和Dropout的随机正则化效果。
数学表达式:
GELU的精确数学定义是
f
(
x
)
=
x
⋅
Φ
(
x
)
f(x) = x \cdot \Phi(x)
f(x)=x⋅Φ(x),其中
Φ
(
x
)
\Phi(x)
Φ(x) 是标准高斯分布(均值为0,方差为1)的累积分布函数 (CDF)。
Φ ( x ) \Phi(x) Φ(x) 可以用误差函数 (erf) 表示: Φ ( x ) = 1 2 [ 1 + erf ( x 2 ) ] \Phi(x) = \frac{1}{2}[1+\text{erf}(\frac{x}{\sqrt{2}})] Φ(x)=21[1+erf(2x)]。
因此,GELU的精确形式为: f ( x ) = x ⋅ 1 2 [ 1 + erf ( x 2 ) ] f(x) = x \cdot \frac{1}{2}[1+\text{erf}(\frac{x}{\sqrt{2}})] f(x)=x⋅21[1+erf(2x)]。
在实践中,也常用以下近似形式:
- 基于Sigmoid的近似: f ( x ) ≈ x ⋅ σ ( 1.702 x ) f(x) \approx x \cdot \sigma(1.702x) f(x)≈x⋅σ(1.702x)
- 基于Tanh的近似: f ( x ) ≈ 0.5 x ( 1 + tanh [ 2 / π ( x + 0.044715 x 3 ) 2 ] ) f(x) \approx 0.5x(1+\tanh[\frac{\sqrt{2/\pi}(x+0.044715x^3)}{\sqrt{2}}]) f(x)≈0.5x(1+tanh[22/π(x+0.044715x3)])
函数图形及其导数图形:
-
函数图形: GELU的图形也是一条平滑的曲线,形状上可以看作是ReLU的一个平滑近似。与ReLU不同,GELU在负值区域并非恒为0,而是有一个小的负值下凹,然后再趋向于0。它也是非单调的。

-
导数图形: GELU的导数(对于精确形式)为 Φ ( x ) + x ⋅ ϕ ( x ) \Phi(x) + x \cdot \phi(x) Φ(x)+x⋅ϕ(x),其中 ϕ ( x ) \phi(x) ϕ(x) 是标准高斯分布的概率密度函数 (PDF)。其导数图形也是平滑的,并且在原点附近表现出一定的复杂性。

输出值域: 近似为 ( ≈ − 0.17 , ∞ ) (\approx-0.17,\infty) (≈−0.17,∞)
优点:
- 结合随机正则化思想: GELU的设计受到了Dropout的启发,它通过乘以高斯CDF来对输入进行随机门控,但这种门控是确定性的,取决于输入值本身的大小(输入值越大,被"保留"的概率越高)。
- 平滑且处处可微: GELU是一个平滑函数,在其整个定义域内都是可微的,这可能有助于优化。
- 性能优越: 在许多自然语言处理(NLP)任务中,尤其是在基于Transformer的模型(如BERT, GPT系列)中,GELU已成为标准配置,并表现出优于ReLU的性能。
- 非单调性: 与Swish类似,GELU的非单调性可能使其能够捕获更复杂的数据模式。
缺点:
- 计算成本较高: 精确的GELU计算涉及到误差函数(erf),近似形式也可能包含tanh或指数运算,因此其计算成本通常高于ReLU及其简单变体。
典型应用场景:
- Transformer模型: GELU是BERT、GPT、ViT等众多基于Transformer架构的模型的标准激活函数。
- 在其他需要高性能激活函数的深度学习模型中也逐渐被采用。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.GELU(approximate='none')(approximate可以是 ‘none’ 或 ‘tanh’) - TensorFlow/Keras:
tf.keras.activations.gelu(x, approximate=True)(approximate默认为True,使用tanh近似) 或在层定义中指定activation='gelu'
4.7 Mish 函数 (Mish Function)
Mish是一种相对较新的自门控激活函数,由Diganta Misra提出,其设计灵感来源于Swish,并声称在多种基准测试中表现优于Swish和ReLU。
数学表达式:
f
(
x
)
=
x
⋅
tanh
(
softplus
(
x
)
)
f(x) = x \cdot \tanh(\text{softplus}(x))
f(x)=x⋅tanh(softplus(x))
其中, softplus ( x ) = ln ( 1 + e x ) \text{softplus}(x) = \ln(1+e^x) softplus(x)=ln(1+ex) 是Softplus函数, tanh ( ⋅ ) \tanh(\cdot) tanh(⋅) 是双曲正切函数。
函数图形及其导数图形:
-
函数图形: Mish函数是一条平滑的、非单调的曲线。其形状与Swish有相似之处,例如在负值区有下凹然后趋于一个小的负常数,正值区无界增长。但Mish的曲率和下界值与Swish不同,通常在负区的下凹更深一些。

-
导数图形: Mish的导数表达式较为复杂,但其图形也是平滑的。

输出值域: 近似为 ( ≈ − 0.3088 , ∞ ) (\approx-0.3088,\infty) (≈−0.3088,∞)
优点:
- 结合多种理想特性: Mish被设计为集平滑、非单调、自门控(self-gated)和自正则化(self-regularized,通过其有下界的特性)等多种有利特性于一身的激活函数。
- 优越的性能: 提出者声称,在大量的图像分类、目标检测等计算机视觉任务以及其他领域的基准测试中,Mish的表现通常优于ReLU、Swish以及其他标准激活函数,能够带来准确率的提升。
- 更好的梯度流和平滑的损失前景: Mish的平滑性和特定的非单调形状据称有助于形成更平滑的损失函数表面,从而易于优化,并促进更好的梯度流动,尤其是在非常深的网络中。
- 无上界,有下界: 与Swish类似,正区无上界避免饱和,负区有下界有助于正则化效果。
缺点:
- 计算成本显著较高: Mish函数涉及到tanh和softplus(包含指数和对数运算)的组合,因此其计算复杂度显著高于ReLU,甚至也高于Swish和GELU。这可能成为其在计算资源受限或对推理速度要求极高的场景中应用的瓶颈。
典型应用场景:
- 作为ReLU、Swish等激活函数的一个潜在高性能替代品,特别是在对模型性能要求较高,且计算成本不是首要制约因素的深度学习模型中。
- 在计算机视觉领域的一些先进模型中有所尝试。
PyTorch/TensorFlow 实现:
Mish通常需要用户自定义实现,因为它可能未被所有主流深度学习框架的最新稳定版直接内置。
其TensorFlow/Keras实现可以写作 x * tf.math.tanh(tf.math.softplus(x))。PyTorch中类似地可以使用 x * torch.tanh(torch.nn.functional.softplus(x))。一些第三方库或最新的框架版本可能已包含Mish的优化实现。
从ReLU的简洁高效,到其变体对特定问题的修正,再到Swish、GELU、Mish等更复杂但可能性能更优的函数的出现,激活函数的设计体现了在表达能力、优化难度和计算效率之间的持续探索和权衡。没有一种激活函数能在所有情况下都表现最佳,因此理解它们各自的特性对于模型设计和调优至关重要。
5. 输出层激活函数专题
神经网络的输出层激活函数的选择与隐藏层有显著不同,它和具体的机器学习任务类型(如回归、二分类、多分类、多标签分类)以及所采用的损失函数紧密相关。输出层激活函数的主要目的是将网络最后一层的原始输出(通常称为logits或得分)转换为符合任务要求的格式。
5.1 Softmax 函数
Softmax函数是专门用于**多分类(multi-class classification)**问题输出层的激活函数,其中每个样本只能属于K个互斥类别中的一个。
原理与数学公式:
Softmax函数接收一个包含K个实数值的向量
z
=
(
z
1
,
z
2
,
.
.
.
,
z
K
)
z=(z_1,z_2,...,z_K)
z=(z1,z2,...,zK)(即logits,对应K个类别的原始得分),并将其转换为一个K维的概率分布向量
p
=
(
p
1
,
p
2
,
.
.
.
,
p
K
)
p=(p_1,p_2,...,p_K)
p=(p1,p2,...,pK)。每个元素
p
i
p_i
pi 表示输入样本属于第
i
i
i 个类别的概率。
其数学公式为:
p
i
=
Softmax
(
z
i
)
=
e
z
i
∑
k
=
1
K
e
z
k
p_i = \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{k=1}^{K} e^{z_k}}
pi=Softmax(zi)=∑k=1Kezkezi
对于向量中的第 i i i 个元素,首先计算其指数 e z i e^{z_i} ezi(确保所有值非负),然后将该值除以所有K个元素指数的总和(进行归一化)。
特性:
- 概率分布输出: Softmax的输出值 p i p_i pi 都在(0, 1)区间内。
- 总和为1: 所有输出概率的总和 ∑ i = 1 K p i = 1 \sum_{i=1}^{K} p_i = 1 ∑i=1Kpi=1,构成一个有效的概率分布。
- 强调最大值: Softmax函数具有"赢者通吃"的特性,它会放大输入logit之间的差异,使得具有最大logit值的类别获得相对较高的概率,而其他类别的概率则相应减小。
- 保持序关系: 输入logit的相对大小关系在输出概率中得以保持,即如果 z i > z j z_i > z_j zi>zj,则通常 p i > p j p_i > p_j pi>pj。
应用:
- 专门用于多分类问题的输出层,其中类别是互斥的。例如,手写数字识别(0-9中的一个数字)、图像分类(猫、狗、鸟中的一个类别)等。
- 通常与分类交叉熵损失函数(Categorical Cross-Entropy Loss)配合使用。
PyTorch/TensorFlow 实现:
- PyTorch:
torch.nn.Softmax(dim=None)(需要指定作用的维度,通常是类别维度) - TensorFlow/Keras:
tf.keras.activations.softmax(x, axis=-1)或在输出层指定activation='softmax'
5.2 Sigmoid 函数 (在输出层)
Sigmoid函数在输出层的应用主要针对二分类和多标签分类问题。
应用:
- 二分类问题 (Binary Classification):
- 当任务是将样本分为两个互斥类别之一时(例如,判断邮件是否为垃圾邮件,肿瘤是良性还是恶性),输出层通常设置一个神经元,并使用Sigmoid激活函数。Sigmoid的输出值在(0,1)之间,可以直接解释为样本属于"正类"的概率 p p p。属于"负类"的概率则为 1 − p 1-p 1−p。
- 这种情况下,通常与二元交叉熵损失函数(Binary Cross-Entropy Loss)配合使用。
- 多标签分类问题 (Multi-label Classification):
- 当一个样本可以同时属于多个类别时(例如,一部电影可以同时被打上"喜剧"、“爱情”、"动作"等多个标签),输出层会为每个可能的标签设置一个独立的神经元。每个神经元都使用Sigmoid激活函数,独立地输出该样本具有对应标签的概率。在这种情况下,各个输出概率之间是相互独立的,它们的总和不一定为1。
- 损失函数通常是逐个标签计算二元交叉熵损失,然后求和或求平均。
5.3 线性函数 (Linear/Identity Function)
线性激活函数,也称为恒等激活函数(Identity function),在输出层主要用于回归问题。
数学公式:
f
(
x
)
=
x
f(x) = x
f(x)=x
特性:
- 线性函数不改变其输入值,直接将其作为输出。输出范围是 ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)。
应用:
- 主要用于**回归问题 (Regression Problems)**的输出层,其中目标是预测一个或多个连续的数值(例如,预测房价、股票价格、温度等)。由于回归任务的输出值可以是任意实数,没有固定的范围限制(除非问题本身有界),线性激活函数能够直接输出网络计算得到的原始预测值,不做任何变换或压缩。
- 回归任务通常使用均方误差(Mean Squared Error, MSE)或平均绝对误差(Mean Absolute Error, MAE)等损失函数。
PyTorch/TensorFlow 实现:
在PyTorch和TensorFlow/Keras中,如果输出层不需要非线性激活(即用于回归),通常在定义最后一层(如 nn.Linear 或 Dense)时不指定 activation 参数,或者显式指定为线性激活(例如,Keras中可以指定 activation='linear',尽管默认不指定激活即为线性)。
5.4 输出层激活函数选择与任务类型的关系
输出层激活函数的选择与机器学习任务的类型密切相关,其根本原因在于任务对输出值的形式和范围有特定要求。
回归任务 (Regression):
- 目标: 预测连续值,其范围可能是无界的(如股票价格)或有界的(如预测百分比)。
- 要求: 输出应能覆盖整个实数范围(或特定有界范围)。
- 选择: 线性激活函数是自然的选择,因为它不改变最后一层线性组合的输出,允许预测值取任何实数值。如果已知输出严格非负,有时也会考虑ReLU,但线性函数更为通用。
二分类任务 (Binary Classification):
- 目标: 将输入分为两个互斥类别之一(如是/否,0/1)。
- 要求: 输出应能表示属于某一类的概率,范围在(0,1)之间。
- 选择: Sigmoid激活函数是标准选择,它将任意实数logit映射到(0,1)区间,完美契合概率的定义。
多分类任务 (Multi-class Classification - Mutually Exclusive):
- 目标: 将输入从多个(K个)互斥类别中选择一个(如数字0-9识别)。
- 要求: 输出应为一个K维向量,其中每个元素表示属于对应类别的概率,所有概率之和为1。
- 选择: Softmax激活函数是标准选择。它接收K个logit值,输出一个K维的概率分布,确保所有输出值在(0,1)之间且总和为1,清晰地表示了输入属于每个互斥类别的概率。
多标签分类任务 (Multi-label Classification - Non-mutually Exclusive):
- 目标: 为输入分配多个标签,每个标签的出现是独立的(如一张图片同时包含猫和狗)。
- 要求: 对每个可能的标签,输出其存在的概率,范围在(0,1)之间,且各标签概率独立,不要求总和为1。
- 选择: 对每个标签对应的输出神经元独立使用Sigmoid激活函数。
此外,输出层激活函数的选择也常常与所使用的损失函数相匹配,以简化梯度计算并确保损失函数能够正确衡量模型预测与真实标签之间的差异。例如,Softmax常与分类交叉熵损失配合,Sigmoid常与二元交叉熵损失配合。这种搭配使得损失函数的梯度形式更为简洁,有利于优化过程。
6. 激活函数的比较与选择指南
在神经网络设计中,选择合适的激活函数对于模型的性能和训练效率至关重要。本章节将对主要的激活函数进行系统性比较,并提供一些实用的选择策略。
6.1 系统性比较
为了更清晰地对比不同激活函数的特性,下表总结了前面章节讨论的主要激活函数(Sigmoid, Tanh, ReLU, Leaky ReLU, PReLU, ELU, SELU, Swish, GELU, Mish)的关键属性。
| 特性 (Property) | Sigmoid | Tanh | ReLU | Leaky ReLU (LReLU α _\alpha α) | PReLU (PReLU a i _{a_i} ai) | ELU (ELU α _\alpha α) | SELU ( λ \lambda λ, α \alpha α) | Swish ( β \beta β) | GELU | Mish |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学表达式 | 1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1 | e x − e − x e x + e − x \frac{e^x-e^{-x}}{e^x+e^{-x}} ex+e−xex−e−x | max ( 0 , x ) \max(0,x) max(0,x) | x x x if x > 0 x>0 x>0, α x \alpha x αx else | x i x_i xi if x i > 0 x_i>0 xi>0, a i x i a_i x_i aixi else | x x x if x > 0 x>0 x>0, α ( e x − 1 ) \alpha(e^x-1) α(ex−1) else | λ ⋅ ELU α ( x ) \lambda \cdot \text{ELU}_\alpha(x) λ⋅ELUα(x) (特定 λ \lambda λ, α \alpha α) | x ⋅ σ ( β x ) x \cdot \sigma(\beta x) x⋅σ(βx) | x ⋅ Φ ( x ) x \cdot \Phi(x) x⋅Φ(x) (高斯CDF) | x ⋅ tanh ( softplus ( x ) ) x \cdot \tanh(\text{softplus}(x)) x⋅tanh(softplus(x)) |
| 导数 (简要) | σ ( x ) ( 1 − σ ( x ) ) \sigma(x)(1-\sigma(x)) σ(x)(1−σ(x)) | 1 − tanh 2 ( x ) 1-\tanh^2(x) 1−tanh2(x) | 1 if x > 0 x>0 x>0, 0 else | 1 if x > 0 x>0 x>0, α \alpha α else | 1 if x i > 0 x_i>0 xi>0, a i a_i ai else | 1 if x > 0 x>0 x>0, ELU α ( x ) + α \text{ELU}_\alpha(x)+\alpha ELUα(x)+α else | λ \lambda λ if x > 0 x>0 x>0, λ α e x \lambda\alpha e^x λαex else | 复杂, 非单调 | 复杂, Φ ( x ) + x ϕ ( x ) \Phi(x)+x\phi(x) Φ(x)+xϕ(x) (高斯PDF) | 复杂, 非单调 |
| 输出值域 | ( 0 , 1 ) (0,1) (0,1) | ( − 1 , 1 ) (-1,1) (−1,1) | [ 0 , ∞ ) [0,\infty) [0,∞) | ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞) | ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞) | ( − α , ∞ ) (-\alpha,\infty) (−α,∞) | ( − λ α , ∞ ) (-\lambda\alpha,\infty) (−λα,∞) | ( ≈ − 0.278 β − 1 , ∞ ) (\approx-0.278\beta^{-1},\infty) (≈−0.278β−1,∞) | ( ≈ − 0.17 , ∞ ) (\approx-0.17,\infty) (≈−0.17,∞) | ( ≈ − 0.3088 , ∞ ) (\approx-0.3088,\infty) (≈−0.3088,∞) |
| 是否零中心 | 否 | 是 | 否 | 近似否 (取决于 α \alpha α) | 近似否 (取决于 a i a_i ai) | 近似是 (可输出负值) | 是 (自归一化至0均值) | 否 | 近似否 | 否 |
| 饱和区域 (梯度趋零) | 两端饱和 | 两端饱和 | 左侧饱和 (x≤0) | 无 (若 α \alpha α=0) | 无 (若 a i a_i ai=0) | 左侧饱和 (趋向 − α -\alpha −α) | 左侧饱和 (趋向 − λ α -\lambda\alpha −λα) | 左侧趋近小负值 | 左侧趋近小负值 | 左侧趋近小负值 |
| 梯度消失风险 | 高 | 中高 | 低 (正区无) | 低 (若 α \alpha α=0) | 低 (若 a i a_i ai=0) | 低 | 非常低 (自归一化) | 低 | 低 | 低 |
| Dying Neuron 问题 | 无 | 无 | 是 | 缓解/无 | 缓解/无 | 缓解/无 | 缓解/无 | 缓解/无 | 缓解/无 | 缓解/无 |
| 计算成本 | 高 (指数) | 高 (指数) | 非常低 | 非常低 | 非常低 | 中高 (指数) | 中高 (指数) | 中高 (Sigmoid) | 高 (erf/tanh) | 非常高 (tanh, softplus) |
| 典型隐藏层应用 | 早期网络, 现少用 | RNNs, 早期网络 | CNNs, FNNs (默认) | ReLU替代 | ReLU/LReLU替代 | ReLU替代 | 深层FNNs (特定条件) | Transformer, CNNs | Transformer (BERT, GPT) | CV, 替代Swish/ReLU |
注:上表中的"复杂"指函数形式或导数形式相对复杂,不易简单概括。 α \alpha α, a i a_i ai, β \beta β, λ \lambda λ 为各函数定义的参数。实际的计算成本和性能会受具体实现和硬件影响。
6.2 选择策略
选择激活函数并没有一个放之四海而皆准的"万能"答案。最佳选择通常取决于具体的任务类型、网络架构的深度和复杂性、数据集的特性以及可用的计算资源。然而,可以遵循一些一般性的经验法则和推荐,并结合实验进行调优。
通用经验法则与推荐:
-
隐藏层首选ReLU及其变体: 对于大多数现代深度神经网络的隐藏层,ReLU通常是首选的默认激活函数。它计算简单、收敛速度快,并能有效缓解梯度消失问题。
-
警惕Dying ReLU: 如果使用ReLU时发现网络训练困难或大量神经元不激活(可以通过监控神经元激活值的稀疏度来判断),可以尝试使用其变体,如Leaky ReLU、PReLU或ELU,它们通过允许负值输入时存在小的非零梯度来解决"Dying ReLU"问题。
-
Sigmoid和Tanh的局限性: Sigmoid和Tanh由于其饱和特性导致的梯度消失问题,在深层网络的隐藏层中已不常使用。Tanh因其零中心化的输出特性,表现通常优于Sigmoid,可能在某些RNN结构或较浅的网络中仍有应用价值。
-
尝试更新的激活函数: 如果计算资源允许且追求更高性能,可以考虑尝试Swish、GELU或Mish等较新的激活函数,它们在许多基准测试中显示出优于ReLU的潜力,尤其是在大型复杂模型中(如Transformer)。
-
按任务特性选择激活函数:
- 对于计算机视觉任务,ReLU及其变体(特别是Leaky ReLU)是最常用的选择。在大型模型中,Swish和Mish也展现出良好性能。
- 对于自然语言处理任务,尤其是Transformer架构,GELU已成为事实上的标准。
- 对于循环神经网络,Tanh仍然是隐藏状态更新的常见选择,而门控单元(如LSTM、GRU)中的门则通常使用Sigmoid。
- 对于超深网络,如果不使用批归一化,可以考虑使用SELU(配合适当的初始化和特定网络结构)。
-
结合实验验证:
- 最终,激活函数的选择应该通过实验验证来确定。可以在小规模模型上比较不同激活函数的表现,选择最佳的应用到完整模型中。
- 关注训练曲线,观察不同激活函数下模型的收敛速度、稳定性和最终性能。
- 在计算资源允许的情况下,可以考虑通过超参数搜索将激活函数类型作为一个超参数来优化。
-
权衡计算效率与模型性能:
- 在资源受限的场景(如移动设备部署或实时推理),应优先考虑计算效率高的激活函数,如ReLU和Leaky ReLU。
- 在追求极致性能的场景(如学术研究或大型商业模型),可以尝试计算成本较高但性能可能更优的激活函数,如Swish、GELU或Mish。
- 在某些情况下,混合使用不同激活函数可能是有益的,如不同层使用不同类型的激活函数。
-
激活函数与其他网络组件的协同:
- 考虑激活函数与其他网络组件(如批归一化、残差连接)的交互。例如,批归一化可以缓解非零中心激活函数(如ReLU)的一些问题。
- 在使用正则化技术时,注意它们与激活函数的兼容性。例如,SELU设计用于与特定的AlphaDropout一起使用。
通过综合考虑以上因素,并针对具体任务和数据进行实验,可以为神经网络选择最适合的激活函数,从而在训练效率、计算成本和模型性能之间取得良好平衡。
7. 激活函数的演进、挑战与前沿研究
随着深度学习的快速发展,激活函数的研究也在不断深入和拓展。本章节将回顾激活函数的发展历程、分析当前面临的挑战,并探讨一些前沿研究方向。
7.1 激活函数的演进历程
激活函数的发展大致可以分为几个阶段,每个阶段都伴随着深度学习领域的重要突破。
7.1.1 早期激活函数(Sigmoid时代)
-
阶跃函数 (Step Function): 最早的人工神经元模型(如感知机)使用阶跃激活函数,即当输入超过阈值时输出1,否则输出0。这种简单的二元激活虽然概念上直观,但由于不可微,难以用于基于梯度的优化。
-
Sigmoid和Tanh: 随着反向传播算法的提出,需要可微的激活函数来支持梯度计算。Sigmoid(逻辑函数)和Tanh(双曲正切)成为主流选择。它们提供了平滑的S型曲线,将输入映射到有界区间。这一时期的神经网络往往较浅(通常只有1-2个隐藏层),因为更深的网络会遇到严重的梯度消失问题。
7.1.2 现代激活函数(ReLU革命)
-
ReLU的突破: 2010年前后,ReLU的广泛应用标志着激活函数研究的一个重要里程碑。相比于Sigmoid/Tanh,ReLU的简单性和在正区间的线性行为使得深度网络训练变得更加高效和稳定。ReLU的成功使得训练很深的神经网络成为可能,尤其是在卷积神经网络中的应用(如AlexNet)直接推动了深度学习的复兴。
-
ReLU变体的涌现: 针对ReLU的缺点(如Dying ReLU问题),研究者们提出了一系列改进版本:Leaky ReLU通过在负区间引入小斜率解决神经元死亡问题;PReLU将负区间斜率参数化为可学习参数;ELU通过负区间的指数函数提供零中心化输出;SELU引入自归一化特性…这些变体都试图在保持ReLU优点的同时,解决其特定问题。
7.1.3 新一代激活函数(复杂非单调函数)
-
基于搜索和优化的激活函数: 随着神经架构搜索(NAS)技术的发展,一些激活函数如Swish是通过算法自动发现的,而非手工设计。这类函数通常具有更复杂的形式,往往是非单调的,在某些任务上表现出优于传统激活函数的性能。
-
特定任务优化的激活函数: 最近的趋势是为特定架构或任务设计定制化激活函数。例如,GELU在Transformer架构中表现出色,成为了BERT、GPT等模型的标准激活函数;Mish针对图像识别任务进行了优化。
-
注意力激活函数: 随着注意力机制的兴起,一些专门用于注意力计算的激活变体也开始出现,如基于GELU的变体在视觉Transformer中的应用。
7.2 当前挑战
尽管激活函数研究取得了显著进展,但仍面临一些重要挑战:
7.2.1 理论理解的局限
-
缺乏统一理论框架: 目前对于为什么某些激活函数(如非单调的Swish和GELU)在特定任务上表现优异的理论解释仍然不足。大多数新激活函数的提出主要基于经验观察和实验验证,而非严格的数学推导。
-
与优化理论的脱节: 激活函数设计与深度学习优化理论之间的联系尚未完全建立。例如,如何设计激活函数使得神经网络的损失景观更加平滑、避免局部极小值等问题仍在探索中。
7.2.2 设计与实现的平衡
-
表达能力与计算效率的权衡: 更复杂的激活函数(如Mish)通常具有更强的表达能力,但同时也带来了更高的计算成本。在实际应用中,特别是资源受限的环境(如移动设备),需要谨慎权衡这种表现提升是否值得额外的计算开销。
-
硬件适配性: 不同激活函数在不同硬件平台(如CPU、GPU、TPU、神经网络加速器)上的实现效率各异。例如,某些硬件可能对分段线性函数(如ReLU)有特殊优化,而对指数运算较慢。
7.2.3 通用性与专用性的矛盾
-
任务依赖性: 目前没有一种"通用最优"的激活函数适用于所有任务和所有网络架构。不同的激活函数在不同任务上可能表现截然不同,这增加了选择的复杂性。
-
超参数敏感性: 一些激活函数(如Leaky ReLU的斜率参数α)引入了额外的超参数,增加了模型调优的复杂度,且最优值通常需要通过实验确定。
7.3 前沿研究方向
激活函数研究的前沿领域正在探索多个有前途的方向:
7.3.1 自适应激活函数
-
动态参数化激活函数: 一些研究提出让激活函数的参数随输入数据动态调整。例如,Dynamic ReLU根据输入自适应地调整其形状参数;FReLU(Funnel ReLU)引入空间感知机制,使激活函数对输入的不同区域有不同的响应。
-
上下文感知激活: 这类激活函数不仅考虑单个神经元的输入,还考虑周围神经元的状态或更广泛的网络上下文。例如,SIREN(Sinusoidal Representation Networks)使用正弦函数作为激活,使网络能更好地表示连续信号和隐式函数。
7.3.2 基于神经架构搜索的激活函数
-
激活函数搜索: 扩展神经架构搜索(NAS)技术,将激活函数形式纳入搜索空间。例如,可以通过组合基本算术运算和非线性变换,自动发现新型激活函数。这方面的代表工作包括发现Swish的研究。
-
层特定激活函数: 为网络中的不同层或不同类型的层(如卷积层、全连接层)搜索最优的激活函数组合,而非使用统一的激活函数。
7.3.3 理论驱动的激活函数设计
-
基于信息论的设计: 从信息论角度优化激活函数,使其能最大化保留输入信息或最有效地传递梯度信息。
-
与初始化和正则化的协同设计: 研究激活函数与权重初始化方法、正则化技术(如Batch Normalization)的相互作用,设计能更好配合特定初始化和正则化策略的激活函数。
7.3.4 激活函数的硬件高效实现
-
量化友好的激活函数: 设计在量化环境(低精度表示,如8位或4位整数)下仍能保持高性能的激活函数,支持边缘设备上的高效推理。
-
神经形态计算激活函数: 为神经形态计算硬件(模拟生物神经系统工作方式的计算设备)设计特定的激活函数,如基于脉冲的激活。
7.3.5 注意力机制中的激活函数创新
-
注意力特化激活: 为Transformer等基于注意力的架构设计专门的激活函数,优化自注意力计算中的非线性变换。
-
激活与注意力的融合: 探索将注意力机制直接融入激活函数设计的可能性,使激活过程本身具有上下文感知能力。
7.4 新兴趋势与未来展望
随着深度学习持续快速发展,激活函数研究也呈现出一些值得关注的新兴趋势:
-
多样化与个性化: 激活函数设计越来越走向多样化和针对特定任务的个性化定制,而非追求单一的通用解决方案。
-
理论与实践结合深入: 激活函数的理论研究正在深化,从经验驱动逐渐向理论驱动转变,但仍保持与实际应用的紧密联系。
-
硬件感知设计: 考虑特定硬件平台特性的激活函数设计正成为一个重要方向,特别是随着专用AI芯片的普及。
-
自动化设计: 激活函数的设计过程将更多地借助自动化工具,如神经架构搜索、自动微分等技术。
未来,随着对神经网络内部工作机制理解的深入,以及新型计算硬件的不断涌现,激活函数的研究将继续蓬勃发展。它可能从当前的"单一函数"概念扩展到更复杂的形式,如条件激活、动态激活网络等。无论形式如何演变,激活函数作为引入非线性和支持丰富表达能力的核心组件,将持续在深度学习的发展中扮演关键角色。

























 1527
1527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








