半桥LLC谐振原理2：基波近似法推导输出输入比

公式推导（基波近似法）

我们只关注方波信号，因为这是我们可以从输入开关电路中得到的。 公式1显示了振幅为A的方波的傅里叶级数。

考虑到中使用的约定，开关电路输出端的电压是一个方波，由公式2表达

此电压是直流电压（Vdc/2） （谐振电容（Cr）对其具有阻隔作用）和无穷多个正弦波之和，这些正弦波的基波是通过公式2计算得出的， 其中k = 1，如公式3中所示。

公式 4 中显示了此正弦电压的峰值、平均值和 rms 值。

如前所述，如果将谐振回路正确调整到开关频率，谐振回路将对基波频率呈现有限阻抗，而对所有其他谐波频率呈现无限（实际上是非常大的）阻抗。结果是谐振回路将流过正弦电流。由于这些电抗元件的原因，电压和电流之间将存在相移，如图 11 中所示。

因此，谐振回路电流可由公式 5 表达。

MOSFET Q1 导通时，从输入电压发生器流出的直流电流可以按一个周期内谐振电流的平均值计算。结果如公式 6 中所示。

利用公式 3、公式 5 和公式 6 可以用图 12 的模型代替“ 实际的 ” 输入电流。左侧电路表示输入：电压来自于发生器 （Vdc）；如图所示，从电压源流出的电流是谐振电流的平均 （直流）值。

右侧部分表示驱动谐振回路的等效电路，我们只关注基波频率下的正弦信号。现在我们还可以确定平均输入功率，如公式 7 中所示：

duty=50%，只有一半的时间导通，所以除以2

实际变压器用其模型代替，其中明确显示了磁化电感（L m）。初级和次级的泄漏电感反而将被忽略（对本讨论不重要） 。根据之前介绍的只关注基波频率下正弦波形的假设，可以得出图 13 中谐振回路的传递函数（H(s)） ，图中的输出电路已被替换为等效电阻（Re） ，我们将在下一节中计算其值。

考虑图 14

可以计算输入阻抗 Zin(s)， 如公式 8 中所示。

如果我们认识到电路元件可以集总到串联阻抗 （Zs： Cr和 Lr）和并联阻抗 （Zp： Lm、变压器和输出负载）中，则可以很容易地计算出电路传递函数。公式 9 到公式 11显示了详细计算过程。

Zs (s) 和 Zp(s) 分别是串联支路和并联支路的阻抗， 公式 9和公式10对它们进行扩展，公式11中显示了计算过程。

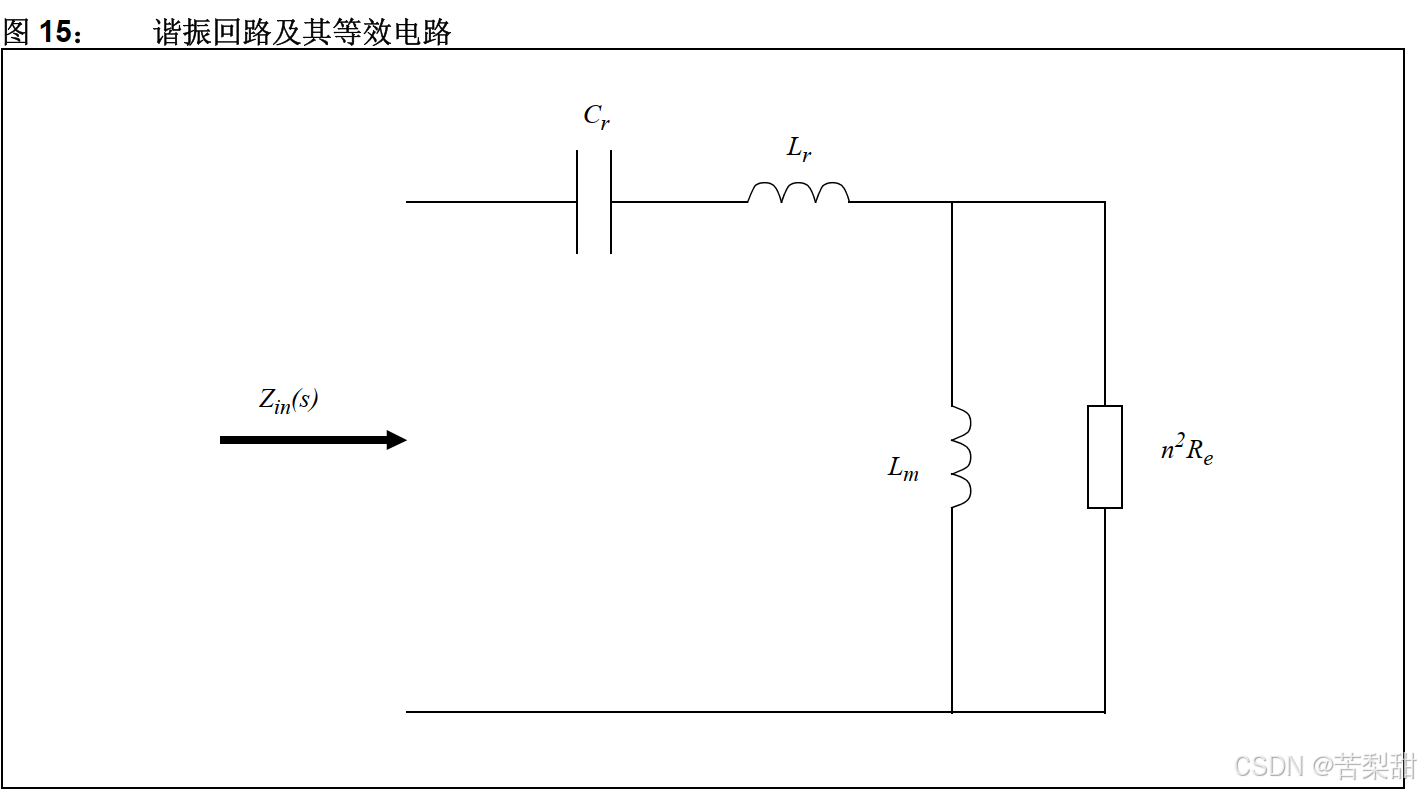
图 13 的电路可以重新绘制为图 16。

在谐振回路中，由于只有基波正弦波形具有相关振幅（所有其他波形均被谐振回路传递函数衰减） ，因此可在基波频率下定义传递函数，如公式 12 中所示。

在这两种情况下，下标 “1” 表示仅考虑基波频率分量。因数 （1/n）取决于次级电压与初级电压的比值，如公式 13 所表达。

再次说明，在变压器次级，由于谐振回路的原因，变压器本身将流过正弦电流（irect(t)）。此电流将根据其符号交替流过两个二极管D3和D4， 如图17和图18中所示。检查电路时，可以通过此电流计算变压器次级的电压值。实际上，根据图 17 和图 18，可以观察到以下情况：

如果电流为正，则 D3 导通， vrect(t) = Vo

如果电流为负，则 D4 导通， vrect(t) = -Vo

以0V为中心考虑此方波的傅里叶级数， 可以写出其分析等式 （整流器输入端），如公式 14 所示。

基波分量如公式 15 所示。

此电压的平均值和 rms 值如公式 16 所示。

如图 19 所示，变压器输出端的正弦电流 irect,1(t) 由二极管整流， 因此流过二极管之后的电流值是等式17的结果。

整流器输入端的电流如公式 18 所表达（仅基波频率） 。

公式 19 显示了整流器输出电流，公式 20 显示了此电流的平均值。

总结：在次级存在一个基波项如公式 15 所示的方波电压，以及一个正弦电流 （公式 18 到公式 20）。这里的重点是这两个信号彼此同相，这意味着在电阻中它们的电压和电流之间的关系相同。因此，可以使用阻值适当的电阻来替代整流器工作。

等效电阻值可以根据公式 16 和求出 Irect,1,pk 的公式 20计算得出，如公式 21 所示。

整流器模型如图 20 中所示。

此时，图 10 中的转换器模型的所有部分均已确定，各部分的传递函数亦计算得出，因此可以确定转换器的总传递函数。

将图 12、图 13、图 14、图 15 和图 20 的框图连接在一起可获得整个模型，如图 21 中所示。由于电路元件是在仅认为基波频率信号重要的情况下定义的，因此模型通常称为一次谐波近似（First Harmonic Approximation， FHA）。

可参考图 21 并通过公式 22 确定整体 I/O 关系，即输出— 输入电压比 （这两个电压是直流值） 。

公式 23 引入了 “ 电压转换比 ” 的定义。结果如公式 24中所示。

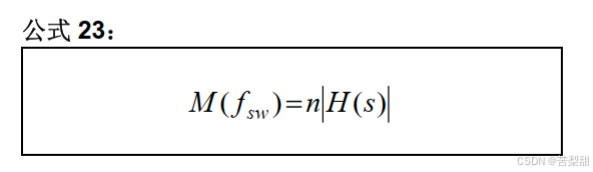
M(fsw)取决于多种不同的参数，我们将在“电压转换比”一节中进行分析。

在继续讨论之前，必须先定义几个稍后将用到的关系。LLC 电路具有两个谐振频率：一个（fr）由于存在 Lr 和Cr而产生（见公式 25）；另一个（见公式 26）由于还存在 Lm 而产生。但此后提到谐振频率时将始终指 fr。

另一个谐振频率如公式 26 中所示。

它用于定义归一化频率，该频率是电流频率 （f）与谐振频率 （fr）的比值，如公式 27 中所示。

之后，所有频率值都被认为是归一化频率。

此外，为方便起见，我们对以下几项进行定义：电感比（见公式 28）、特性阻抗 （见公式 29）以及品质因数（见公式 30） 。

使用公式 12 和公式 23 可以计算出电压传送比的分析表达式。结果如公式 31 中所示。

换句话说，传送比是归一化频率与谐振元件值的复数函数。此外，对于特定设计，必须先计算出所有参数，才能得出 M(fsw) 函数。但是，可以考虑以单个参数 λ和 Q生成一系列 M 曲线。

电压转换比与增益曲线分析

图 22 表示了这样一条曲线。在此图中，清楚地显示了fr 谐振频率。另一个谐振频率（fr2）是左侧（低频）出现高峰值的原因。图 23 绘出了 Q = 0.2（固定值）以及 λ在0.1到0.9之间变化且步幅为0.1时的一系列曲线。 图24 绘出了 λ = 0.2 （固定值）以及品质因数 Q 在 0.1 到0.9 之间变化且步幅也为 0.1 时的曲线。

关于这些图有几点说明。显然，随着  的增大，曲线越来越尖锐；而 Q 不断增大时，曲线越来越平坦。

转换器设计为在标称输入电压下以谐振频率工作。根据公式 24，转换器的工作方式以公式 32 表示，求解后如公式 33 所示。

观察图 23 和图 24 中的曲线，可以看到一个基本特性：在任何情况下，所有曲线都始终在同一点 （对应于fn = fr，即谐振时）互相交叉；该点处的电压转换比为 1 （在使用建议的匝数比时）。 这意味着这样选择n将保证在标称条件下，无论系统当前的特定 M 曲线如何，都将产生正确的输出电压。

图 25 绘出了电路输入阻抗（公式 11 中定义的 Zin）。在此图中，部分区域突出显示，这是频率轴中（f n 时）输入阻抗呈现正斜率的一部分。请记住，电感的传递函数具有同样的行为，我们可以确定输入电路和正弦输入电压波形将 LLC 电路看作电感。 这对于转换器实现非常小的（导通）开关损耗来说极其重要，我们将在后面的章节进行介绍。相反地，图最左侧的 Zin 的斜率为负，这表示系统具有电容特性。这也表示 Z 曲线上的一个点在容性和感性等效特性之间定义了一个边界。可以看出，如果是复数函数，输入阻抗 Zin 的结果为公式 34。