《Infinity: 扩展基于比特的自回归建模以实现高分辨率图像合成》学习笔记

种花生的图图

已于 2025-01-30 14:05:21 修改

阅读量1k

点赞数 20

分类专栏：生成式模型文章标签：人工智能机器学习算法深度学习神经网络

于 2024-12-23 21:21:47 首次发布

本文链接：https://blog.csdn.net/weixin_56848903/article/details/144501130

版权

生成式模型专栏收录该内容

12 篇文章

订阅专栏

paper：https://arxiv.org/pdf/2412.04431

GitHub：GitHub - FoundationVision/Infinity: Infinity ∞ : Scaling Bitwise AutoRegressive Modeling for High-Resolution Image Synthesis

一、 Introduction

1、背景与挑战：

视觉生成技术近年来取得了快速进展，实现了高质量、高分辨率的图像与视频合成。文本到图像生成是其中最具挑战性的任务之一，因为它需要复杂的语言理解和精确的场景构建。目前，视觉生成主要分为两种方法：扩散模型（Diffusion Models） 和 自回归模型（AutoRegressive Models）。

（1）扩散模型（Diffusion Models）

扩散模型通过反转数据向随机噪声的正向路径进行训练，通过连续的去噪过程生成图像。
这类模型在生成高质量图像方面表现出色，能够逐步改善图像细节。

（2）自回归模型（AutoRegressive Models）

自回归模型借鉴了语言模型的扩展能力和泛化能力，通过视觉标记器（visual tokenizer）将图像转换为离散标记（tokens），并通过下一个标记预测或下一个尺度预测的方式进行图像生成。
但是自回归模型具有以下问题：重建质量不足：使用离散标记时，重建图像的质量低于连续标记。缺乏细节：生成的视觉内容细节不如扩散模型丰富。生成效率低：由于采用逐步光栅扫描（raster-scan）进行标记预测，生成延迟较高。

（3）视觉自回归建模（VAR）

VAR（Visual AutoRegressive）最近重新定义了图像上的自回归学习，将其视为粗到细的“下一个尺度预测”（next-scale prediction）。
与扩散模型相比，VAR 在泛化能力和扩展能力上表现出色，且所需的生成步骤更少。VAR 能够利用大型语言模型（LLMs）的扩展能力，并在细化前一步预测时受益于扩散模型的优势。

（4）VAR的挑战

量化误差：自回归模型中的索引式离散标记器（index-wise discrete tokenizer）存在严重的量化误差，特别是在高分辨率图像的重建中难以捕捉细节。
监督模糊：索引标记在生成阶段容易产生模糊监督，导致图像细节丢失和局部扭曲。
训练与测试分布差异：由于自回归模型依赖于教师强制训练（teacher-forcing），在测试时累积误差放大，进一步影响视觉细节质量。

2、主要贡献：

提出了一种称为二进制建模（Bitwise Modeling）的新方法，通过全流程使用二进制标记取代传统的索引式标记。这个二进制建模框架由三个核心模块组成：二进制视觉标记器（Bitwise Visual Tokenizer）、二进制无限词汇表分类器（Bitwise Infinite-Vocabulary Classifier）和二进制自纠错机制（Bitwise Self-Correction）。

（1）比特级建模（Bitwise Modeling）：

核心改进在于用比特级标记替代索引级标记。传统方法中，大词汇表的离散标记需要一个整数索引表示，这种方式在词汇表扩展时会带来优化和计算上的挑战。通过将大整数分解为二进制比特，模型可以直接操作比特级标记，从而显著降低复杂度。

（2）分词器词汇表扩展（Vocabulary Expansion）：

Infinity 的词汇表大小达到了 $2^{64}$ ，远超以往的自回归模型。这种超大规模词汇表不仅能够细化视觉表示，还能实现接近连续分词器的性能（如 VAEs）。

（3）比特级自纠正（Bitwise Self-Correction）：

模型通过随机翻转部分比特来模拟预测错误，并重新量化残差特征，增强了系统的自我纠正能力。这种机制提高了模型的鲁棒性，使其能更好地适应不确定性。如图所示，本文将传统的令牌预测从一个大整数转换为二进制位，在一个按位无限词汇分类器中，以解决优化和计算挑战，使视觉自回归模型中的大量词汇学习成为可能。

左侧：传统分类器（Conventional Classifier）

传统分类器直接预测索引（index labels），其索引的范围为 $2^{d}$ ，即 d 位二进制表示的所有可能组合。
示例：如果 d = 4，则索引范围是 [0, 15]，共有 $2^{4}$ = 16个索引值。

缺点：
当连续特征发生轻微扰动（perturbation）时，比如 [0.01 → 0.1]，可能会导致索引发生剧烈变化（例如从 9 变为 1）。
随着 d 的增加，索引值范围呈指数级增长，对应的分类器参数也会急剧增大。
例如，当 d = 32 和 h = 2048 时，参数量达到 8.8万亿，这超出了当前的计算能力。

右侧：无限词汇分类器（Infinite-Vocabulary Classifier，IVC）

IVC不直接预测索引，而是逐位预测量化特征（bit labels）。
例如，对于 [-1, +1, -1, +1]，IVC直接预测其量化的位值。

优点：
由于预测的是量化后的特征值，轻微的连续特征扰动仅引起量化特征的细微变化，因此预测更稳健。
参数量与 d 呈线性增长（而非指数增长），当 d = 32 和 h = 2048 时，IVC只需 0.13M（13万）参数，远低于传统分类器。

二、Related work

1、自回归模型（AutoRegressive Models）

自回归模型利用上下文信息预测下一个标记（token），并逐步生成目标输出。
在视觉任务中，自回归模型通过离散图像分词器将图像分割成一系列索引级标记（tokens），再通过 Transformer 逐步预测这些标记，最终生成完整图像。

离散图像分词器（Discrete Tokenizers）：
将图像分割成小块并量化为离散标记（tokens）。
解码器 Transformer：
通过索引预测逐步生成图像，类似于文本生成任务中的下一个单词预测（next-token prediction）。

基于向量量化（VQ-based）的方法使用向量量化技术将图像块（image patches）转换为索引级标记（index-wise tokens），并使用仅包含解码器的 Transformer（decoder-only transformer）来预测下一个标记的索引。然而，这些方法受到以下限制：

缺乏大规模的 Transformer 模型；
向量量化自动编码器（VQ-VAE）[64] 固有的量化误差（quantization error）。

VAR 重新定义了图像生成的任务，将传统的“逐步生成像素或标记”方式替换为“逐尺度预测（next-scale prediction）”：

逐尺度预测：
不直接预测像素，而是预测不同层次或尺度上的图像特征，捕获全局视觉信息结构。
改进效果：
显著提升了生成图像的质量和采样速度。

2、扩散模型（Diffusion Models）

扩散模型是一种基于去噪学习的生成方法。它模拟数据分布的逆扩散过程（reverse diffusion process），通过逐步去噪生成高质量的样本。

去噪学习机制（Denoising Learning Mechanisms）： 扩散模型的核心是通过学习噪声的分布来逐步还原数据分布，这一机制的优化（如[27, 41]）显著提升了生成图像的质量。
采样效率（Sampling Efficiency）： 由于扩散模型生成样本需要多个步骤（迭代），采样效率成为限制其实际应用的关键问题。相关研究（如[53, 52, 38, 39, 4]）通过优化采样过程，减少生成时间。

潜在扩散模型引入了在潜在空间（latent space）中建模的概念，相较于直接在像素空间建模，潜在空间的表示更加紧凑且计算效率更高。

DiT 引入了一种更加可扩展的 Transformer 架构用于扩散建模，相比传统的卷积网络方法，Transformer 能更好地捕获全局特征。

3、模型扩展（Scaling Models）

扩展定律指出，模型的性能（如测试集的交叉熵损失）与以下三个变量之间存在幂律关系：

模型规模（Model Size）： 参数量越大，模型的性能越强（前提是有足够的数据和计算资源支持）。
数据集规模（Dataset Size）： 数据越多，模型的表现越好。
计算资源（Compute）： 提供足够计算力可以更充分地训练大模型。

三、Infinity Architecture

1、Infinity 框架

Infinity 模型的核心框架如下图所示，展示了其主要组成部分以及运行过程，包含 比特级自纠正（Bitwise Self-Correction）、因果视觉自回归 Transformer（Causal VAR Transformer） 和 多尺度视觉分词器（Multi-Scale Visual Tokenizer）。

输入包括 文本提示（Text Input） 和 目标图像（Ground Truth, GT）。文本提示通过交叉注意力机制进行指导预测。

视觉分词器首先将图像 $I$ 编码为特征图 $F \in \mathbb{R}^{h \times w \times d}$ （步长为 $s$ ），然后将特征图 $F$ 量化为 $K$ 个多尺度的残差图 $(R_1, R_2, ..., R_K)$ 。第 $k$ 级的残差图的分辨率为 $h_k \times w_k$ ，其分辨率从 $k = 1$ 到 $K$ 逐渐增大。基于这一系列的残差图，我们可以通过如下公式逐步逼近连续特征 $F$ ：

$F_{k}=\sum_{k}^{i=1}up(R_{i},(h,w))$

其中， $\text{up}(\cdot)$ 表示双线性上采样（bilinear upsampling）， $F_k$ 是累积上采样的 $R_{\leq k}$ 。

这部分的过程实际上就是上一篇论文VAR的特征量化过程。

伪代码如下：

随后，Transformer 以自回归方式学习在前一尺度的预测结果和文本输入的条件下，预测下一尺度的残差 $R$ 。自回归的概率可以形式化表示为：

$p(R_1, \dots, R_K) = \prod_{k=1}^{K} p(R_k \mid R_1, \dots, R_{k-1}, \Psi(t))$

其中， $\Psi(t)$ 是提取的文本嵌入。 $(R_1, ..., R_{k-1}, \Psi(t))$ 是预测 $R_k$ 时的前缀上下文。此外，文本嵌入 $\Psi(t)$ 通过交叉注意力机制进一步引导预测过程。

具体来说，如上图所示，文本嵌入 $\Psi(t) \in \mathbb{R}^{L \times C}$ 被投影为一个 $\langle SOS \rangle \in \mathbb{R}^{1 \times 1 \times h}$ 作为第一尺度的输入，其中 $h$ 是 Transformer 的隐藏维度。在第一尺度，Transformer 基于 $\langle SOS \rangle$ 预测 $R_1$ 。在第 $k$ 尺度，为了匹配输入特征和输出标签 $R_k$ 的空间大小，我们将前一尺度 $k-1$ 的下采样特征 $\tilde{F}_{k-1}$ 作为输入来预测 $R_k$ ，公式如下：

$\tilde{F}_{k-1}=down(F_{k-1},(h_{k},w_{k}))$

其中， $\text{down}(\cdot)$ 表示双线性下采样， $\tilde{F}_{k-1}$ 和 $R_k$ 的空间大小均为 $(h_k, w_k)$ 。下面伪代码展示了获取二值量化结果和 Transformer 输入的详细过程。

$F$ 输入的原始特征图。

${(h^r_1, w^r_1), ..., (h^r_K, w^r_K)}$ 定义了多尺度残差图的分辨率 $(h_k, w_k)$ ，用于逐步生成多尺度残差 $R_k$ 和下采样特征 $\tilde{F}_k$ 。

$R_{\text{queue}} = []$ 初始化一个队列，用于存储多尺度的残差比特标签（bit labels）。

$F_{\text{queue}} = []$ 初始化一个队列，用于存储输入给 Transformer 的特征。

从 $k=1$ 到 $K$ ，依次处理每个尺度。

$R_{k}=Q(down(F-F_{k-1},(h_{k},w_{k})))$ ： $F - F_{k-1}$ 表示当前特征 $F$ 减去前一尺度的累积特征 $F_{k-1}$ ，得到当前尺度的残差。down表示对残差进行双线性下采样，使其符合当前尺度 $(h_k, w_k)$ 的分辨率。Q表示对下采样后的残差进行量化，得到当前尺度的二值残差 $R_k$ 。

$QueuePush(R_{queue},R_{k})$ ：将 $R_k$ 添加到残差队列 $R_{\text{queue}}$ 中。

$F_{k}=\sum_{i=1}^{k}up(R_{i},(h,w))$ ： $\text{up}(R_i, (h, w))$ 表示对残差 $R_i$ 进行双线性上采样到原始分辨率 $(h, w)$ 。累积和： 当前尺度的累积特征 $F_k$ 是所有尺度残差 $R_1$ 到 $R_k$ 的上采样累积结果。

$\tilde{F}_{k}=down(F_{k},(h_{k+1},w_{k+1}))$ ：累积特征 $F_k$ 进行双线性下采样，使其符合下一尺度 $(h_{k+1}, w_{k+1})$ 的分辨率。

$QueuePush(\tilde{F}_{queue},\tilde{F}_{k})$ ：将 $\tilde{F}_{k}$ 添加到特征队列 $F_{queue}$ 中。

$R_{\text{queue}}$ ：多尺度残差队列,存储所有尺度的残差比特标签 $R_1, R_2, ..., R_K$ 。

$F_{\text{queue}}$ ：Transformer 输入特征队列,存储所有尺度的下采样特征 $\tilde{F}_1, \tilde{F}_2, ..., \tilde{F}_K$ ，作为 Transformer 的输入。

在先前基于索引（index-wise）的表示方法中，预测的形状为 $(h_k, w_k, V_d)$ ，其中 $V_d$ 是视觉分词器的词汇大小。当使用二值量化（binary quantization）且代码嵌入维度为 $d$ 时， $V_d = 2^d$ 。当 $d$ 较大时，所需的计算资源变得难以承受。

为了更好的理解，这里放一张 VAR 的 transformer 训练图，与infinity 进行对比。

文生图的VAR 和传统VAR 看架构区别，似乎就是 $\langle SOS \rangle$ 不同，传统VAR 的 $\langle SOS \rangle$ 是文章设置的，文生图的VAR 是由text 转换的。

2、Visual Tokenizer

扩展词汇表的规模可以显著提高图像重建和生成的质量。但是直接扩大现有分词器的词汇表会大幅增加内存消耗和计算负担，导致实际不可行。本文提出了 比特级多尺度残差量化器（Bitwise Multi-Scale Residual Quantizer），通过降低内存需求支持超大规模词汇表（例如 $2^{64}$ ），从而充分发挥离散分词器的潜力。

（1）核心思想：

用 比特级量化器（Bitwise Quantizer） 替代传统的向量量化器（Vector Quantizer）。

优点：

与输入维度无关（Dimension-Independent）。
大幅减少计算复杂度和内存需求。

（2）量化公式

在多尺度量化器的第 $k$ 层，将连续残差向量 $z_k \in \mathbb{R}^d$ 量化为二值输出 $q_k$ ，公式如下：

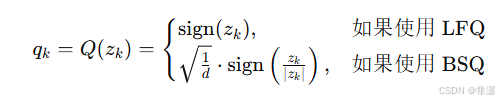
LFQ（Logistic Function Quantizer）：直接对向量 $z_k$ 取符号（正为 $+1$ ，负为 $-1$ ）。

BSQ（Binary Spherical Quantizer）：将向量 $z_k$ 归一化为单位向量（单位化），sign （二值化），并加上一个常数 $\sqrt{\frac{1}{d}}$ （缩放因子）。

LFQ 是一种 简单直接的比特级量化方法，其核心思想是直接对输入特征向量 $z_{k}$ 的每个元素应用符号函数（sign function）进行二值化。

BSQ 是一种 改进型的比特级量化方法，通过加入 单位化（normalization） 和 缩放因子，解决了 LFQ 的计算复杂度和内存需求问题，同时提升了量化的稳定性。

量化器	优点	缺点
LFQ	简单直接，通过符号函数量化	计算复杂度 $O(2^d)$ ，当维度 $d$ 较大时（例如 $d=20$ ），可能会导致内存不足（OOM）
BSQ	输入输出均为单位向量，计算复杂度仅为 $O(d)$ ，支持超大规模词汇表（如 $2^{64}$ ）	相比 LFQ，多了归一化操作，计算稍复杂。

我们可以发现，BSQ 的复杂度为 $O(d)$ ，显著低于 LFQ 的 $O(2^d)$ 。即使代码簿大小达到 $2^{64}$ ，BSQ 的内存需求也没有明显增加。

（3）熵惩罚（Entropy Penalty）

为了均匀利用代码簿中的所有值，引入熵惩罚项：

$L_{entropy}=E[H(q(z))]-H[E(q(z))]$

其中， $q(z)$ ：对输入 $z$ 进行量化后的离散输出分布（比如比特级表示）。

$H(\cdot )$ ：熵函数，用于衡量一个分布的不确定性或多样性。

$E(\cdot)$ ：期望值运算符，表示对分布的平均值。

第一项 $\mathbb{E}[H(q(z))]$ ： 计算分布 $q(z)$ 的熵在所有样本上的期望。

第二项 $H[\mathbb{E}(q(z))]$ ： 计算量化分布的均值的熵。

熵惩罚的目的是让模型尽可能使用更多的比特组合，避免代码簿利用率过低。

3、无限词汇分类器

IVC(Infinite-Vocabulary Classifier) 用 $d=log_{2}(V_{d})$ 个二值分类器替代传统的 $V_{d}$ 类分类器，将指数级计算复杂度降低到线性级别。每位比特的预测相互独立，不受其他位的影响。即使某些维度特征接近 0，其他维度仍然可以提供清晰的监督信号。