Mixtral 8x7B 模型详解包括原理、图表和代码

最新推荐文章于 2025-05-04 16:09:00 发布

数智笔记

最新推荐文章于 2025-05-04 16:09:00 发布

阅读量1k

点赞数 3

分类专栏：大语言模型文章标签：人工智能语言模型

本文链接：https://blog.csdn.net/wjjc1017/article/details/136221315

版权

大语言模型专栏收录该内容

195 篇文章

订阅专栏

本文详细介绍了Mixtral模型，特别是其稀疏专家混合(SMoE)、滑动窗口注意力(SWA)、旋转位置编码(RoPE)和分组查询注意力(GQA)等关键特性。这些技术有助于提高模型效率和性能，使得Mixtral在参数数量和计算量上超越了Llama和GPT-3.5。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

自 2023 年底以来，Mixtral 8x7B[1] 在大型语言模型领域变得非常流行。它之所以受欢迎，是因为它在参数数量（小于 8x7B）和计算量（小于 2x7B）方面优于 Llama2 70B 模型，甚至在某些方面超过了 GPT-3.5。

本文主要关注代码，并包含插图来解释 Mixtral 模型的原理。

整体架构

Mixtral 模型的整体架构与 Llama 和其他仅解码器模型类似，可以分为三个部分：输入嵌入层、多个解码器块和语言模型解码头。如图 1 所示。

图 1：Mixtral 模型的整体架构。作者提供的图片。

解码器层

解码器层的架构如图 2 所示。每个解码器层主要由两个模块组成：注意力和稀疏专家混合（SMoE）。

图 2：解码器层。作者提供的图片。

我们可以看到，Mixtral 模型还包括额外的特性，如稀疏专家混合（SMoE）、滑动窗口注意力（SWA）、分组查询注意力（GQA）和旋转位置嵌入（RoPE）。

接下来，本文将解释这些重要特性。

稀疏专家混合（SMoE）

从图 1 和图 2 中，我们已经知道了 SMoE 在整个模型架构中的位置。在本节中，让我们更详细地看一下 SMoE 的内部结构。在这里，SMoE 模块被单独提取出来，如图 3 所示。

图 3：SMoE 模块。作者提供的图片。

如图 3 所示，输入到模型的每个标记在经过注意力层和残差连接后，随后会通过门控或路由器（Gating or Router）定向到前 k 个专家（默认情况下，k = 2）。

然后，最相关的专家的输出被加权和求和，然后通过残差连接传递，以获得当前解码器层的输出。

首先，让我们来看一下专家的代码：

class MixtralBLockSparseTop2MLP(nn.Module):
    def __init__(self, config: MixtralConfig):
        super().__init__()
        self.ffn_dim = config.intermediate_size
        self.hidden_dim = config.hidden_size

        self.w1 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)
        self.w2 = nn.Linear(self.ffn_dim, self.hidden_dim, bias=False)
        self.w3 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)

        self.act_fn = ACT2FN[config.hidden_act]

    def forward(self, hidden_states, routing_weights):
        current_hidden_states = self.act_fn(self.w1(hidden_states)) * self.w3(hidden_states)
        current_hidden_states = self.w2(current_hidden_states)
        return routing_weights * current_hidden_states

一旦我们有了一个专家，MixtralSparseMoeBlock 将默认情况下的 8 个专家组合在一起（self.num_experts = 8）。门控层为每个标记选择前 2（默认情况下k = 2）个专家模型进行计算。你可以在这里找到这部分代码。 https://github.com/huggingface/transformers/blob/v4.36.2/src/transformers/models/mixtral/modeling_mixtral.py

class MixtralSparseMoeBlock(nn.Module):
    """
    This implementation is
    strictly equivalent to standard MoE with full capacity (no
    dropped tokens). It's faster since it formulates MoE operations
    in terms of block-sparse operations to accomodate imbalanced
    assignments of tokens to experts, whereas standard MoE either
    (1) drop tokens at the cost of reduced performance or (2) set
    capacity factor to number of experts and thus waste computation
    and memory on padding.
    """

    def __init__(self, config):
        super().__init__()
        self.hidden_dim = config.hidden_size
        self.ffn_dim = config.intermediate_size
        self.num_experts = config.num_local_experts
        self.top_k = config.num_experts_per_tok

        # gating
        self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)
        # Experts
        self.experts = nn.ModuleList([MixtralBLockSparseTop2MLP(config) for _ in range(self.num_experts)])

    def forward(self, hidden_states: torch.Tensor) -> torch.Tensor:
        """ """
        batch_size, sequence_length, hidden_dim = hidden_states.shape
        hidden_states = hidden_states.view(-1, hidden_dim)
        # router_logits: (batch * sequence_length, n_experts)
        # Retrieve the scores provided by each expert, 
        # with the dimensions of batch * sequence * num_experts, 
        # and then select the topk experts.
        router_logits = self.gate(hidden_states)

        routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)
        routing_weights, selected_experts = torch.topk(routing_weights, self.top_k, dim=-1)
        
        # After obtaining the scores of the top k experts, 
        # it is necessary to normalize them again. 
        # This step is important to assign appropriate weights to 
        # the results calculated for the subsequent experts
        routing_weights /= routing_weights.sum(dim=-1, keepdim=True)
        # we cast back to the input dtype
        routing_weights = routing_weights.to(hidden_states.dtype)

        final_hidden_states = torch.zeros(
            (batch_size * sequence_length, hidden_dim), dtype=hidden_states.dtype, device=hidden_states.device
        )

        # One hot encode the selected experts to create an expert mask
        # this will be used to easily index which expert is going to be sollicitated
        expert_mask = torch.nn.functional.one_hot(selected_experts, num_classes=self.num_experts).permute(2, 1, 0)

        # Loop over all available experts in the model and perform the computation on each expert
        for expert_idx in range(self.num_experts):
            # Choose the expert you are currently using
            expert_layer = self.experts[expert_idx]
            # Select the index corresponding to the current expert
            # top_x actually corresponds to the current expert's token index.
            idx, top_x = torch.where(expert_mask[expert_idx])

            if top_x.shape[0] == 0:
                continue

            # in torch it is faster to index using lists than torch tensors
            top_x_list = top_x.tolist()
            idx_list = idx.tolist()

            # Index the correct hidden states and compute the expert hidden state for
            # the current expert. We need to make sure to multiply the output hidden
            # states by `routing_weights` on the corresponding tokens (top-1 and top-2)
            current_state = hidden_states[None, top_x_list].reshape(-1, hidden_dim)
            # The expert model will use selected states to perform 
            # calculations and multiply them by the weight
            current_hidden_states = expert_layer(current_state, routing_weights[top_x_list, idx_list, None])

            # However `index_add_` only support torch tensors for indexing so we'll use
            # the `top_x` tensor here.
            # Add the output of each expert to the final result according to their index.
            final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))
        final_hidden_states = final_hidden_states.reshape(batch_size, sequence_length, hidden_dim)
        return final_hidden_states, router_logits

为了增强理解，我在代码中添加了一些注释。

上述代码可以分为 3 个主要步骤：

对于输入，门控层用于获取路由信息。在使用 softmax 对路由信息进行归一化后，选择前 k 个权重和专家的索引。然后将索引转换为称为 expert_mask 的稀疏矩阵。
遍历所有专家，并执行以下操作：选择专家，每个专家只需要处理自己的标记。
为了获得输出，计算所选专家的输出的加权和。

滑动窗口注意力（SWA）

在传统的自注意力机制中，序列中的每个标记与其他每个标记进行交互，导致时间和空间复杂度为 O(n²)，其中 n 是输入序列的长度，如图 4(a) 所示。一旦我们需要处理更长的文本，这将导致显著的计算负担。

图 4：全注意力和滑动窗口注意力。来源：[2]

因此，为了解决这个困境并使 Transformer 适用于更长的文本，Longformer[2] 提出了以下滑动窗口注意力机制。

如图 4(b) 所示，对于序列中的一个标记，滑动窗口注意力设置了一个固定大小的滑动窗口，表示为 w。它指定序列中的每个标记只能与 w 个标记进行交互，每侧有 w/2 个标记。在此窗口内执行自注意力。这将时间复杂度从 O(n²) 降低到 O(n * w)。

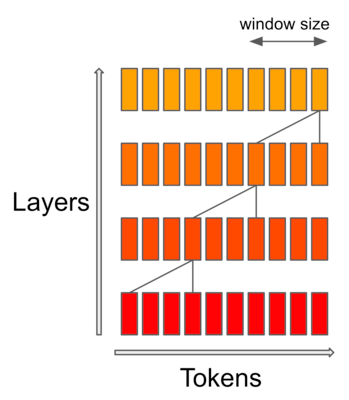
图 5：SWA 的感受野。来源：[3]。

以下是 Mixtral 中用于生成注意力掩码的代码：https://github.com/huggingface/transformers/blob/v4.36.2/src/transformers/modeling_attn_mask_utils.py

@dataclass
class AttentionMaskConverter:

    ...
    ...  

    @staticmethod
    def _make_causal_mask(
        input_ids_shape: torch.Size,
        dtype: torch.dtype,
        device: torch.device,
        past_key_values_length: int = 0,
        sliding_window: Optional[int] = None,
    ):
        """
        生成用于双向自注意力的因果掩码。
        """
        bsz, tgt_len = input_ids_shape
        mask = torch.full((tgt_len, tgt_len), torch.finfo(dtype).min, device=device)
        mask_cond = torch.arange(mask.size(-1), device=device)
        mask.masked_fill_(mask_cond < (mask_cond + 1).view(mask.size(-1), 1), 0)

        mask = mask.to(dtype)

        if past_key_values_length > 0:
            mask = torch.cat([torch.zeros(tgt_len, past_key_values_length, dtype=dtype, device=device), mask], dim=-1)

        # 如果需要，添加下三角滑动窗口掩码
        if sliding_window is not None:
            diagonal = past_key_values_length - sliding_window + 1

            context_mask = 1 - torch.triu(torch.ones_like(mask, dtype=torch.int), diagonal=diagonal)
            mask.masked_fill_(context_mask.bool(), torch.finfo(dtype).min)

        return mask[None, None, :, :].expand(bsz, 1, tgt_len, tgt_len + past_key_values_length)

旋转位置编码（RoPE）

旋转位置编码（RoPE）是许多大型语言模型中使用的一种流行的位置编码技术。它有效地将旋转向量的概念用于位置编码，并使用复数运算来实现。

分组查询注意力（GQA）

GQA[4] 可以看作是多查询注意力（MQA）和多头注意力（MHA）的中间或广义形式：

当 GQA 中只有一组时，称为 MQA。
当 GQA 中的组数等于注意力头数时，称为 MHA。

图 6 清晰展示了这种关系。

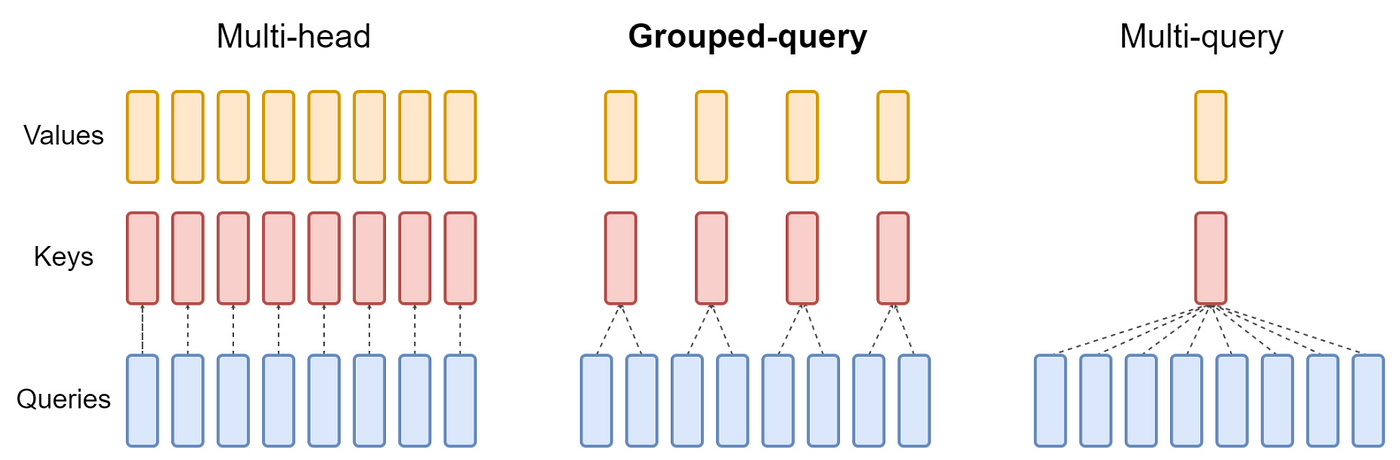
图 6：来源：[4]。

结论

Mixtral-8x7B 是第一个经过验证有效的开源 MoE LLM。它表明 MoE 可以成功实现，并且在相同激活值下优于密集模型。

MoE 是一个极具前景的研究方向，我们期待未来在这一领域取得进一步的进展。

参考文献

[1]: Mistral AI 团队。Mixtral of experts（2023）。网址：https://mistral.ai/news/mixtral-of-experts/。

[2]: I. Beltagy, M. Peters, A. Cohan。Longformer: The Long-Document Transformer（2020）。arXiv 预印本 arXiv:2004.05150。

[3]: Mistral AI 团队。Mistral Transformer（2023）。网址：https://github.com/mistralai/mistral-src。

[4]: J. Ainslie, J. Lee-Thorp, M. Jong, Y. Zemlyanskiy, F. Lebrón, S. Sanghai。GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints（2023）。arXiv 预印本 arXiv:2305.13245。