【论文译文】提升Transformer模型的动态可组合多头注意力机制

最新推荐文章于 2025-05-07 17:16:48 发布

数智笔记

最新推荐文章于 2025-05-07 17:16:48 发布

阅读量2.2k

点赞数 9

分类专栏：大语言模型文章标签： transformer 深度学习人工智能

本文链接：https://blog.csdn.net/wjjc1017/article/details/139089017

版权

大语言模型专栏收录该内容

195 篇文章

订阅专栏

提升Transformer模型的动态可组合多头注意力机制

Github：https://github.com/Caiyun-AI/DCFormer
论文地址：https://arxiv.org/abs/2405.08553

Improving Transformers with Dynamically Composable Multi-Head Attention

Abstract

多头注意力（Multi-Head Attention，MHA）是Transformer模型中的关键组件。在MHA中，各个注意力头独立工作，会导致注意力分数矩阵的低秩瓶颈以及头部冗余等问题。我们提出了一种称为动态可组合多头注意力（Dynamically Composable Multi-Head Attention，DCMHA）的注意力架构，该架构在参数和计算方面都很高效，通过动态组合注意力头来解决MHA的缺点并增强模型的表现力。DCMHA的核心是一个Compose函数，它能根据输入动态地变换注意力分数和权重矩阵。DCMHA可以作为MHA的直接替代品应用于任何Transformer架构，从而形成相应的DCFormer。在不同架构和模型规模的语言建模任务中，DCFormer显著优于Transformer，性能相当于计算量约为 $\sim 1.7 \times-2.0 \times$ 的模型。例如，DCPythia-6.9B在预训练困惑度和下游任务评估上均优于开源的Pythia-12B。代码和模型可在https://github.com/Caiyun-AI/DCFormer获得。

1. Introduction

Transformers （Vaswani等人，2017年）已成为各领域和任务的最先进模型，也是基础模型的事实标准支撑。多头注意力（MHA）是Transformer的重要组成部分，负责标记间的信息交流。MHA允许模型同时关注来自不同表示子空间和不同位置的信息。MHA的一个重要特性是多个注意力头并行且相互独立地工作。尽管这种设计简单且经验上成功[^0]，但也导致了一些问题，例如注意力分数矩阵的低秩瓶颈（Bhojanapalli等人，2020年；2021年）减少了表现力，并且头部冗余问题（Voita等人，2019年；Michel等人，2019年）造成了参数和计算资源的浪费。

文献中有许多工作试图通过引入某种形式的头部之间的交互或协作来改善MHA。我们从头部组合的角度对这些工作进行分类，并从固定数量的“基础头”中组合新头。

头部组合可以在MHA计算图的不同位置进行。一种常见的头部组合形式是使用更复杂的方式组合/选择多个头部的输出，以取代MHA的简单连接然后投影的方法，这种方法可以是静态的（Ahmed等人，2017年）或动态的（Li等人，2019年；Zhang等人，2022年）。尽管这种操作是在MHA计算的最高层次上进行的，但它只是一种“表面”形式的组合：头部仍然各自操作，标记间的底层信息流保持不变。由于这个特点，它通常较轻量且高效，但增加的表现力有限。

在最低层次上的另一种对比方法是组合MHA头部的线性投影 $W^{Q}, W^{K}$ 和 $W^{V}$ （Cordonnier等人，2020年；Liu等人，2022年）。投影组合允许真正新的头部与实际改变的信息流组合，这对于表现力的根本改进是必要的。尽管理论上通过在投影之间共享参数更具参数效率，但这种方法在实践中通常会带来很大的计算成本。此外，组合是静态的，缺乏对输入的适应性。头部组合的潜力不能完全发挥。

我们采用第三种中间方法，即组合注意力分数和/或注意力权重矩阵（本文统称为注意力矩阵）（Shazeer等人，2020年；Wang等人，2022年；Nguyen等人，2022年）。注意力矩阵组合在一定程度上与投影组合有等价关系（参见第2节），确保相比于头部输出组合具有根本性的表现力改进。由于相比于投影组合计算成本较小并经过精心设计，我们能够使组合动态化：新的头部在飞行中根据输入动态组合，进一步增加了模型的表现力。与现有工作相比，我们力求同时满足真正的组合性、动态性和效率的要求（参见表1）。

表1. 各种头部组合方法的比较。（*: 参数高效但计算低效）

在这项工作中，我们提出了一种参数和计算效率高的注意力架构——动态组合多头注意力(DCMHA)，该架构通过动态组合注意力头来解决 MHA 的不足，并增加模型的表现力。DCMHA 的核心是一个 Compose 函数，它以输入依赖的方式转换注意力得分矩阵和权重矩阵。DCMHA 可以作为任何 Transformer 架构中 MHA 的直接替代，从而得到相应的 DCFormer。我们实现了 DCMHA / DCFormer，并进行分析和广泛实验，以评估其有效性、效率和可扩展性。实验结果表明，DCFormer 在不同架构（原始架构或高级 LLaMA 架构）和模型规模（从 405M 到 6.9B）下在语言建模方面明显优于 Transformer，性能与计算量 $\sim 1.7 \times-2 \times$ 的模型相当。例如，DCPythia-6.9B 在预训练困惑度和下游任务评估上均优于开源的 Pythia-12B。我们还将 DCMHA 应用于视觉 Transformer 进行图像分类，并对使用合成数据集的 DCPythia-6.9B 模型进行了初步分析，以更好地理解 DCMHA 的工作原理及效果。

2. 通过转换注意力矩阵进行头部组合

如第 1 节所述，DCMHA 通过组合注意力矩阵实现头部组合。在本节中，我们介绍注意力矩阵组合的概念，展示其在增加模型表现力方面的作用，并讨论其与投影组合的关系。

符号假设 $T$ 和 $S$ 分别是查询和键序列长度。我们用 $A_{h} \in \mathbb{R}^{T \times S}$ 表示第 $h$ 个头的注意力矩阵，它可以是由具有 $H$ 个头的 MHA 模块计算的注意力得分（softmax 之前）或权重（softmax 之后）矩阵。我们可以将 $H$ 个注意力矩阵堆叠成一个张量 $A=\operatorname{Stack}\left(\left\{A_{h}\right\}_{h=1}^{H}\right) \in \mathbb{R}^{H \times T \times S}$ 。我们用 $A_{: i j}=A[:, i, j] \in \mathbb{R}^{H}$ 表示查询向量 $Q_{i}$ 和键向量 $K_{j}$ 之间的注意力向量。

通过注意力矩阵组合，我们可以按如下方式组合出 $H$ 个新的注意力矩阵 $\left\{A_{h}^{\prime}\right\}_{h=1}^{H}$ ：第 $h$ 个组合矩阵 $A_{h}^{\prime}$ 是 $H$ 个基础矩阵的线性组合： $A_{h}^{\prime}=$ $\sum_{j=1}^{H} C_{h j} A_{j}$ ，其中 $\in \mathbb{R}^{H \times H}$ 是组合图。

我们通过图 1 中的几个简化的原型组合图来说明矩阵组合的功能（此例中假设我们在组合注意力权重矩阵）。不同的组合图模式有不同的功能。图 1 (a) 显示了互相激发（Head 3 和 Head 8 之间）和抑制（Head 2 和 Head 5 之间）的情况。当两个头正相关时，互相激发是有帮助的：如果一个头活动，另一个也应该活动。相反，互相抑制的效果是相反的。图 1 (b) 显示了一对多的共享，其中 Head 6 将其注意力权重共享给 Head 4 和 Head 7。图 1 © 显示了多对一的共享，其中 Head 3 和 Head 7 将其权重共享给 Head 1。假设 Head 1 具有一个 OV 电路，可以将具体名词转换为其上位词/超类（例如“apple” → “fruit”），但由于其 QK 电路效率低，可能难以在上下文中正确应用转换。在注意力权重组合的帮助下，它现在可以“借用”来自 Head 3 和 Head 7 的注意力权重，以正常功能运作。即，一个新的头部与 Head 3 和 Head 7 的 QK 电路以及 Head 1 的 OV 电路组合。图 1 (d) 显示了自我激发（Head 3 和 Head 6）和抑制（Head 4）。当一个头在特定上下文中被认为是有益/有害时，这很有用。这里没有跨头部交互，通常称为门控。注意到 $\times H$ 组合图适用于所有 $Q_{i}$ 和 $K_{j}$ 对之间的注意力向量 $A_{: i j}$ ，就像输入和输出通道维度为 $H$ 的 $1 x 1$ 卷积（图 1 (e)）。

既然我们知道可以通过注意力矩阵组合来做什么，实际上我们可以组合 MHA 的 $W^{Q / K / V / O}$ 投影来实现同样的效果。定理 2.1（证明见附录 B）表明，组合注意力得分矩阵等效于通过将现有投影 $\left\{W_{i}^{Q}, W_{i}^{K} \in \mathbb{R}^{D_{m} \times D_{h}}\right\}_{i=1}^{H}$ 连接起来组成具有 $H$ 倍头部维度的新查询[^1] 和键投影 $\left\{\tilde{W}_{i}^{Q}, \tilde{W}_{i}^{K} \in \mathbb{R}^{D_{m} \times H D_{h}}\right\}_{i=1}^{H}$ （ $D_{m}$ 是模型维度。 $D_{h}$ 是头部维度。假设投影没有偏置）：

$$
\begin{equation*}

\tilde{W}{i}^{Q} = \underset{j \in [H]}{\operatorname{Concat}}\left[ C{i j} W_{j}^{Q} \right], \tilde{W}{i}^{K} = \underset{j \in [H]}{\text { Concat }}\left[ W{j}^{K} \right] \tag{1}
\end{equation*}
$$

定理 2.1

通过组合映射 $\in \mathbb{R}^{H \times H}$ 将注意力分数 $\left\{ A_{i} \right\}_{i=1}^{H}$ 组合起来等价于通过公式 (1) 定义的 $Q K$ 投影组合，并进行 $H$ 倍扩展。

类似地，我们也有一个定理来说明权重矩阵组合和以下 OV 投影组合之间的等价关系：

$\begin{equation*} \tilde{W}_{i}^{V} = \underset{j \in [H]}{\operatorname{Concat}}\left[ C_{i j} W_{j}^{V} \right], \tilde{W}^{O} = \operatorname{Tile}\left( W^{O},(H, 1) \right) \tag{2} \end{equation*}$

其中 $\tilde{W}_{i}^{V} \in \mathbb{R}^{D_{m} \times H D_{h}}, \tilde{W}^{O} \in \mathbb{R}^{H H D_{h} \times D_{m}}$ 是组合并扩展后的投影矩阵。 $\operatorname{Tile} \left(W^{O},(H, 1)\right)$ 会将 $W^{O}$ 沿其第一维度重复 $H$ 次。

定理 2.2

通过组合映射 $\in \mathbb{R}^{H \times H}$ 将注意力权重 $\left\{ A_{i} \right\}_{i=1}^{H}$ 组合起来等价于通过公式 (2) 定义的 OV 投影组合，并进行 $H$ 倍扩展。

图 1. 8 个头的简化和原型组合映射及其功能。亮色表示较大的值。

注意力矩阵组合与基于扩展的投影组合之间的关系也支持了它的有效性：Bhojanapalli 等人 (2020) 已经表明，增加 $\mathrm{QK}$ 投影的头维度可以缓解注意力分数矩阵的低秩瓶颈。我们认为，增加 OV 投影的头维度可以提高头部的跨字段信息传输带宽。因此，注意力分数和注意力权重的组合都能够从根本上提升模型的表达能力。

值得注意的是，上述分析基于一个假设，即注意力矩阵组合是静态的，即对所有 $\times S$ 的注意力向量 $\left\{A_{: i j}\right\}$ 应用一个共享的组合映射 $C$ （这是一个可训练参数，可以看作是一个 $\times 1$ 的卷积核）。当为了额外的表达能力增益而使组合变得动态时，即每对查询和键都会有一个各自的组合映射（即输入依赖的内核局部卷积），这就没有等价的投影组合了。这说明注意力矩阵组合比投影组合更通用和灵活。

3. 动态组合多头注意力

在多头注意力（MHA）中，注意力向量 $A_{: i j}$ 控制查询 $Q_{i}$ 和键 $K_{j}$ 之间的信息流。动态组合多头注意力（DCMHA）的核心是一项 Compose 函数，该函数基于 $Q_{i}$ 和 $K_{j}$ 将它们的注意力向量 $A_{: i j} \in \mathbb{R}^{H}$ 转换为带有可训练参数 $\theta$ 的新向量 $A_{: i j}^{\prime}$ ：

$\begin{equation*} A_{: i j}^{\prime}=\operatorname{Compose}(A_{: i j}, Q_{i}, K_{j} ; \theta) \tag{3} \end{equation*}$

总体来看，要实现 DCMHA，我们只需在计算 MHA 时插入两个 Compose 函数，其中文件依赖的跨头互作用会发生，分别应用于 softmax 前的注意力分数张量 $A^{S}$ 和 softmax 后的注意力权重张量 $A^{W}$ （见图 2 [a]）：

$\begin{align*} & A_{i}^{S}=\frac{Q W_{i}^{Q}(K W_{i}^{K})^{T}}{\sqrt{D_{h}}} ; A^{S}=\operatorname{Stack}(A_{1}^{S}, \ldots, A_{H}^{S}) \\ & A^{S}=\operatorname{Compose}(A^{S}, Q, K ; \theta_{\text {pre }}) \\ & A^{W}=\operatorname{Softmax}(A^{S}, \operatorname{dim}=-1) \tag{4}\\ & A^{W}=\operatorname{Compose}(A^{W}, Q, K ; \theta_{\text {post }}) \\ & O_{i}=A_{i}^{W}(V W_{i}^{V}) ; O=\operatorname{Concat}(O_{1}, \ldots, O_{H}) W^{O} \end{align*}$

其中 $W_{i}^{Q}, W_{i}^{K}, W_{i}^{V} \in \mathbb{R}^{D_{m} \times D_{h}}$ 是第 $i$ 个头的投影矩阵， $W^{O} \in \mathbb{R}^{H D_{h} \times D_{m}}$ 是输出投影矩阵。我们沿第一个维度进行 Stack 操作，沿最后一个维度进行 Concat 操作。这里我们使用了 Eqn. (3) 中的“批处理版本”的 Compose 函数，给定 $T$ 个查询和 $S$ 个键，分别打包成矩阵 $\in \mathbb{R}^{T \times D_{m}}$ 和 $\in \mathbb{R}^{S \times D_{m}}$ ，从而将其注意力张量 $\in \mathbb{R}^{H \times T \times S}$ 转换为具有相同形状的新张量。
现在我们描述 Compose 内部的计算过程（图 2 (b)）。 $A_{: i j}$ 分别通过五个分支转换后再相加。首先， $A_{: i j}$ 通过一个独立于 $Q_{i}$ 或 $K_{j}$ 的权重矩阵 $W_{b}$ 投影。这可以看作是一个基础组成，在此基础上叠加了动态组成。在第二个分支中， $A_{: i j}$ 首先被 $w_{q 1} \in \mathbb{R}^{H \times R}$ 投影到较低的维度 $R$ ，然后再通过 $w_{q 2} \in \mathbb{R}^{R \times H}$ 投影回原来的维度 $H$ ，得到 $A_{: i j} w_{q 1} w_{q 2}$ 。动态权重 $w_{q 1}$ 和 $w_{q 2}$ 是从 $Q_{i}$ 计算得出的。这种方法建模了头部如何相互共享它们的注意力分数/权重。通过让 $\ll H$ （在本工作中我们设置 $R = 2$ ），我们假设尽管在头部之间的共享方式有很多，但对于任何特定的查询和键对来说，少数几种共享模式就足够了。在第三个分支中， $A_{: i j}$ 与一个门控 $w_{q g} \in \mathbb{R}^{H}$ 按元素相乘，这个门控也是从 $Q_{i}$ 计算得出的。这个分支控制每个头在给定查询下保留或忘记其原始分数的程度。

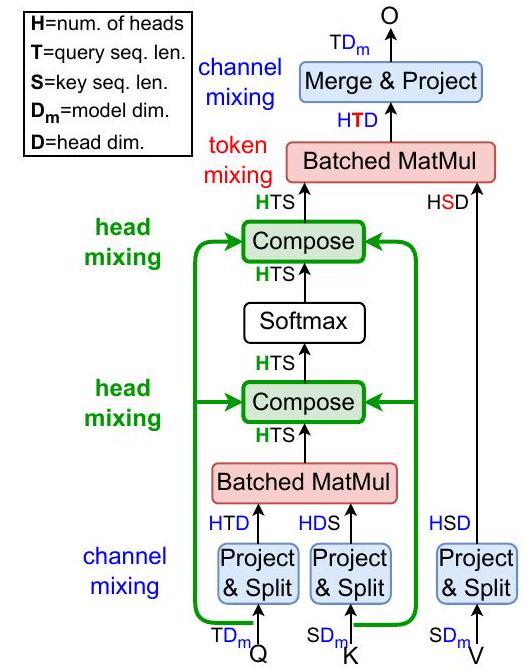
(a) DCMHA 的整体架构

(b) Compose 的计算过程

图 2. DCMHA 的示意图。(a) 省略了缩放和可选的掩码操作。每个线性投影的输入和输出用它们的维度表示，并且投影（即混合）维度是有颜色的。(b) 注意力向量 $A_{: i j}$ 可以是注意力分数或权重。

为了从 $Q_{i}$ 计算动态投影权重 $w_{q 1}$ 和 $w_{q 2}$ ，我们使用了一个具有单隐藏层和 GELU 激活函数的 FFN，其参数为 $W_{q 1} \in \mathbb{R}^{D_{m} \times I}$ 和 $W_{q 2} \in \mathbb{R}^{I \times I}$ ，其中 $I = 2 H R$ 。我们在将 $w_{q 1}$ 乘以 $A_{: i j}$ 之前，沿着 head 的数量维度应用 RMSNorm 而不进行缩放，以稳定训练：
$\begin{align*} & w_{q 1}, w_{q 2}=\operatorname{Chunk}\left(\operatorname{GELU}\left(Q_{i} W_{q 1}\right) W_{q 2}, \operatorname{dim}=1\right) \\ & w_{q 1}=\operatorname{Rmsnorm}\left(\operatorname{Reshape}\left(w_{q 1},(H, R)\right), \operatorname{dim}=0\right) \tag{5}\\ & w_{q 2}=\operatorname{Reshape}\left(w_{q 2},(R, H)\right) \end{align*}$
为了从 $Q_{i}$ 计算动态门控权重 $w_{q g}$ ，我们简单地使用一个线性投影，它的参数为 $W_{q g} \in \mathbb{R}^{D_{m} \times H}$ ，然后使用一个 tanh 非线性函数：
$\begin{equation*} w_{q g}=\tanh \left(Q_{i} W_{q g}\right) \tag{6} \end{equation*}$
对于 $K_{j}$ ，还有两个对称的分支，计算过程和 $Q_{i}$ 相同。五个分支的输出相加，得到最终更新后的向量：
$\begin{array}{r} A_{: i j}^{\prime}=A_{: i j} W_{b}+A_{: i j} w_{q 1} w_{q 2}+A_{: i j} \otimes w_{q g} \tag{7}\\ +A_{: i j} w_{k 1} w_{k 2}+A_{: i j} \otimes w_{k g} \end{array}$
DCMHA 的可训练参数为 $\theta=$ $\left\{W_{b}, W_{q 1}, W_{q 2}, W_{q g}, W_{k 1}, W_{k 2}, W_{k g}\right\}$ 。这些参数与模型的其他参数一起端到端地学习。

3.1 张量分解视角

为了进行动态头组合，我们需要每个 $Q_{i}$ 和 $K_{j}$ 对应的形状为 $\times H$ 的 $\times S$ 变换矩阵（即组合映射）。换句话说，我们需要计算一个输入依赖的 4-D 变换张量 $\in \mathbb{R}^{T \times S \times H \times H}$ 并将其应用于 3-D 注意力张量 $\in \mathbb{R}^{H \times T \times S}$ 。虽然理论上有很多方法可以做到这一点，但不同的方法可能在效率上有很大差异。上述描述的 Compose 的计算等效于对 $W$ 进行两级分解，以提高参数和计算效率：
$\begin{aligned} & A_{: i j}^{\prime}=A_{: i j} W_{i j} \quad i \in[1, T], j \in[1, S] \end{aligned}$

$\begin{align*} & W=W_{b}+\underbrace{\mathcal{W}_{q}}_{\text {row-wise }}+\underbrace{\mathcal{W}_{k}}_{\text {column-wise }} \tag{8} \end{align*}$

我们可以看到函数 $\operatorname{ED}(\cdot, \operatorname{dim})$ 代表 ExpandDims。方程(8) 可以视为方程(7) 的"批处理版本"。首先， $W$ 被分解成一个 2D 张量 $W_{b} \in \mathbb{R}^{H \times H}$ 和两个 3D 张量 $\mathcal{W}_{q} \in \mathbb{R}^{T \times H \times H}$ 和 $\mathcal{W}_{k} \in \mathbb{R}^{S \times H \times H}$ ，其中 $W_{b}$ 是与输入无关的静态权重（作为参数）并起到偏差的作用，而 $\mathcal{W}_{q}$ 和 $\mathcal{W}_{k}$ 则分别是与查询（按行）和键（按列）相关的动态权重。我们称之为行加列分解。然后，每个 3D 张量进一步被分解成两个张量的乘积构成的低秩张量[^3] $\mathcal{W}_{q / k 1} \in \mathbb{R}^{T / S \times H \times R}$ 和 $\mathcal{W}_{q / k 2} \in \mathbb{R}^{T / S \times R \times H}$ 以及由一个 2D 张量 $\mathcal{W}_{q / k g} \in \mathbb{R}^{T / S \times H}$ 填充的对角张量。这种分解形式也被用在其他地方（Zhao et al., 2016; Gu et al., 2021a），称为低秩加对角分解。行加列分解使得可以单独将 $\mathcal{W}_{q}$ 和 $\mathcal{W}_{k}$ 应用于注意力张量 $A$ ，而不需要具体化大的 4D 张量 $W$ 。低秩加对角分解将注意力向量变换矩阵的大小从 $H^{2}$ 减少到 $2 H R + H$ 。由于这些分解，结果张量比 $W$ 小得多，并且可以从输入的查询和键中高效计算。例如， $\mathcal{W}_{q g}=\tanh \left(Q W_{q g}\right)$ （方程(6) 的批处理版本）。

我们通过实验发现，在四个动态分支的存在下，静态基投影（图 2 中的分支 1）可以被简单的跳过连接（即直接将 $A_{: i j}$ 添加到最终的求和中）所替代，性能只有轻微下降（参见第 4.6 节）。在实际操作中，为了更简单和更有效的设计，我们这么做了。DCMHA 的完整伪代码见附录 D。

3.2. Grouped Composition for Tensor Parallel Training

在 Megatron 风格的张量并行（TP）训练中，一层的注意力头被划分成若干组，每组的头都放置在一个节点上，在该节点上进行这些头的计算。在一个典型的 TP 设置中（例如 $H =$ $32, TP = 4$ ），与其跨 32 个头进行组合，不如在每组 8 个头内进行组合（每组头的动态投影秩 $R$ 可以设置为较小的数值 1）。由于组合在每个节点内部本地化进行，头之间没有跨组交互，因此 DCMHA 并未引入额外的跨节点通信。这种分组组合可以通过对 Compose 的简单修改来实现。我们实施了分组 DCMHA 并在 TP 训练中进行了测试。实验结果表明，无论是性能还是速度方面，分组组合与全头组合差别不大。

3.3. Complexity Analysis

表 2 显示了引入 DCMHA 后额外参数和计算的比例，包括分析结果和典型具体值。导出过程在附录 E 中详述。额外参数的比例，即 DCMHA 的 $\theta_{\text {pre }}$ 和 $\theta_{\text {post }}$ 的参数数量除以整个模型的参数数量，与 head dim $D_{h}$ 成反比，对于常用的 $D_{h}$ 值（如 128），该比例可以忽略不计。额外计算的比例，即两次复合函数的 FLOPs 除以整个前向传播的 FLOPs，除了和 $D_{h}$ 成反比外，还随 $\rho=S / D_{m}$ 增加，其中 $S$ 是序列长度，并且对于足够大的模型（如 $\geq 6.9$ B）以及典型的 $S$ 值（如 $\leq S \leq 8192$ ），该比例也非常小。

表 2. DCMHA 引入的额外参数和计算的比例：（最后一行）分析结果和（上几行）典型模型结构和超参数的具体值。 $\mathrm{L}=$ 层数， $\mathrm{S}=$ 序列长度。

4. Experiments

实现细节

我们在 JAX 中实现了 DCFormer 模型和训练。与一些其他工作（Brown et al., 2020; Beltagy et al., 2020; Black et al., 2021）类似，我们为 DCMHA 的每层使用滑动窗口长度为 256 个 token 的本地注意力机制。这种方法提高了效率，而不影响效果。我们使用标准差分别为 $/(\sqrt{2 H R}(H+R))$ 和 $\sqrt{2 /\left(D_{m}+H\right)}$ 的常规初始化器来初始化动态投影/门控生成参数 $W_{q 2}, W_{k 2}$ 和 $W_{q g}, W_{k g}$ 。这样可以确保动态投影和门控权重在训练开始时具有足够小的值，这对于成功训练至关重要。对于 DCMHA 的其他参数，我们使用 Xavier 正态初始化器。

组织结构

由于语言建模可以说是当前基础模型最重要的任务，我们主要关注通过自回归语言建模来评估 DCFormer，采用仅包含解码器的架构，并在预训练指标（损失和困惑度）的扩展曲线（4.1 节）以及大规模训练下的下游任务评估（4.2 节）上进行测试。我们在所有语言建模实验中使用 Pile 数据集（Gao et al., 2020）。然后，为了更好地理解 DCFormer 的工作原理和原因，我们在部分激励了 DCMHA 设计的合成数据集上评估训练后的模型，并分析其投影矩阵（4.3 节）。接下来，4.4 节量化了由合成操作引起的 DCFormer 的训练和推理开销。为了验证 DCMHA 的优势是否在不同的 Transformer 架构和模态中均适用，在第 4.5 节中，我们评估了 DCFormer 应用于用于 ImageNet-1K 分类的仅包含编码器的视觉 Transformers 的性能。最后，第 4.6 节探讨了 DCMHA 的各个组件。除非另有说明，否则 DCFormer 和对比的 Transformer 始终使用相同的实验设置。

4.1. 扩展规律

设置表 3 详细列出了扩展实验的模型大小和超参数。模型架构、学习率和批大小大多取自 GPT-3 规范（Brown et al., 2020）。与 GPT-3 不同，我们解耦了输入和输出的嵌入矩阵。我们以上下文长度 2048 进行训练，并设置训练 token 的数量大致符合 Chinchilla 扩展规律（Hoffmann et al., 2022），该规律规定训练 token 数应与模型大小成正比。其他超参数见附录 C。我们将 DCMHA 应用于两种 Transformer 架构：GPT-3 使用的原始架构（Transformer）和 LLaMA 使用的改进架构（Touvron et al., 2023），后者采用旋转位置编码（RoPE）（Su et al., 2024）和 SwiGLU MLP（Shazeer, 2020）（Transformer++），这是我们已知的最强的 Transformer 架构。

表3. 扩展实验的模型大小和超参数。

结果图 3（顶部）显示了 Transformer(++) 和 DCFormer(++) 模型在 Pile 数据集上的验证损失扩展曲线。DCMHA 显著提升了从 405M 到 1.4B 模型的 Transformer 和 Transformer++ 性能。例如，通过拟合 Transformer 和 Transformer++ 数据点的直线，可以估算出 DCFormer 834M 达到了消耗 $1.87× \times$ 计算量的 Transformer 的损失，而 DCFormer+±834M 则达到了消耗 $1.67× \times$ 计算量的 Transformer++ 的损失。图 3（底部）显示，与 Transformer++ 中的 RoPE 和 SwiGLU MLP 组合相比，DCMHA 相对于基准模型的相对改善幅度（ $\Delta$ 损失）随着计算量的增加减少得较少，显示出 DCMHA 作为架构改进的有利扩展属性。

4.2. 大规模训练和下游评估

设置我们将 DCFormer 与著名的 Pythia 模型套件（Biderman et al., 2023）在大规模训练（Pile 上 300B tokens）下进行比较。具体来说，我们训练了两个模型，DCPythia-2.8B 和 DCPythia-6.9B，并将它们与 Pythia-2.8B, 6.9B 和 12B 进行比较。除了用 DCMHA 替换 MHA 并加入 QKNorm（Dehghani et al., 2023）来稳定训练之外，DCPythia 完全使用与 Pythia 相同的架构选择（例如并行注意力和 MLP， $1/4$ 头大小的旋转嵌入）和训练超参数（例如优化器设置，学习率调度，批大小，上下注释方法） (详情参见 Biderman et al. (2023) 附录 E)。通过这些限制，我们的目标不是获得最先进的结果，而是清楚地量化 DCMHA 带来的增益。

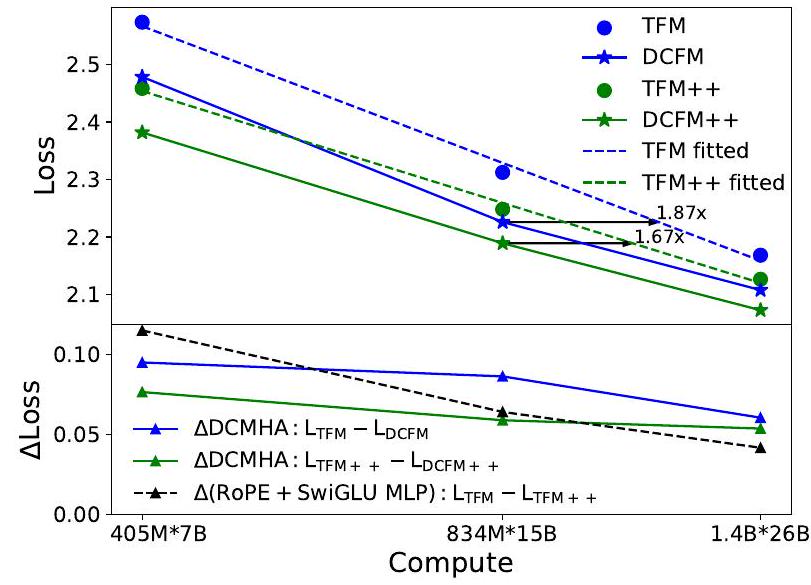
Figure 3. (top) Transformers 和 DCFormers 的缩放曲线。 (bottom) RoPE + SwiGLU MLP 和 DCMHA 相对改进的缩放曲线。TFM++ $=$ TFM + RoPE + SwiGLU MLP；DCFM = TFM + DCMHA；DCFM++ = TFM++ + DCMHA。

Figure 4. Pythia 和 DCPythia 的缩放曲线。

Evaluation Datasets

除了 Pythia 用于下游评估的数据集（LAMBADA (Paperno et al., 2016), PIQA (Bisk et al., 2020), WinoGrande (Sakaguchi et al., 2021), ARC easy and challenge (Clark et al., 2018), SciQ (Welbl et al., 2017), LogiQA (Liu et al., 2020)），我们还包括了 BoolQ (Clark et al., 2019) 和 HellaSwag (Zellers et al., 2019) 用于常识推理，RACE (Lai et al., 2017) 用于阅读理解，所有这些都是广泛使用的基准测试数据集。我们使用 LM evaluation harness (Gao et al., 2023) 评估零样本学习和五样本学习。

Results

除了如图 Figure 4 和表格 Table 4 所示的较低的 Pile 验证损失和困惑度之外，DCPythia 在 $\mathrm{~B}$ 和 $\mathrm{~B}$ 规模上的下游任务准确性上显著优于 Pythia。值得注意的是，DCPythia-6.9B 在困惑度（ppl）和下游任务评估上都优于 Pythia-12B。表格 Table 4 还报告了 Flan Collection 数据集 (Longpre et al., 2023) 随机抽样子集的困惑度。我们抽取了 320K 个示例并计算目标区间的损失。该数据集包含了指令跟随、上下文少量样本学习、链式推理等数据。在 Flan 上，DCPythia 和 Pythia 之间的 ppl 差距显著大于 Pile，这表明 DCMHA 在提高大语言模型的这些重要新兴能力方面更具优势 (Wei et al., 2022)。

表格 Table 4. 对下游 NLP 任务的零样本和五样本评估。

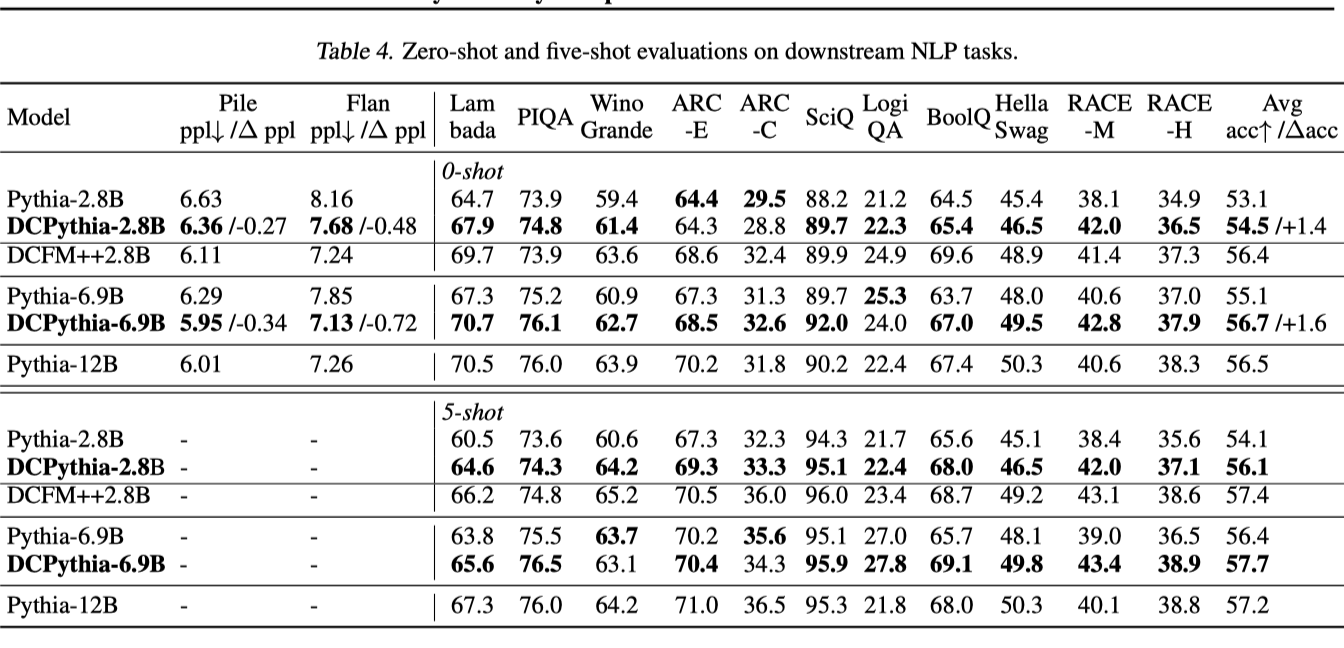
同时可以观察到，在困惑度和下游评估上，由 DCMHA 带来的相对改进（ $\Delta$ Pile ppl, $\Delta$ Flan ppl, $\Delta$ avg acc）随着 6.9 B 模型一般比 2.8 B 模型大，再次表明 DCMHA 在规模扩展上表现良好。为了展示 DCMHA 在 $\mathrm{~B}$ 规模的 Transformer++ 上同样有效，我们还训练了一个 2.8B DCFormer++ 模型 DCFM++2.8B，其结果显著优于 DCPythia-2.8B。

4.3. 合成任务与训练模型权重分析

为了强调模型的动态头部组成能力，我们构建了一个合成数据集，包括一组任务。为了成功预测某些任务中的示例的答案 (最后一个词)，例如“John has an apple. Mary has a dog. So John has a kind of …”，模型必须同时完成两件事：通过查找同一个人来关注正确的源标记’苹果’，并在将其移动到目标标记’of’的残差流时应用正确的转换（对象->超类）到标记嵌入。通过对注意力模式 (例如，同一个人、他人、不同集合中) 和转换 (例如 obj->超类，城市->国家）进行各种组合，我们总共构建了 74 个任务和 888 个示例。更多数据集示例见附件 F。我们推测，基于 MHA 的模型，其中头部具有固定的 QK（用于关注源标记）和 OV（用于转换标记）电路，在解决这类任务时会有一定困难。

我们在合成数据集上测试了 Pythia-6.9B 和 DCPythia-6.9B，并在表格 Table 5 中报告了结果。我们发现：1) 虽然这个数据集看起来简单，但对两个模型都具有挑战性；2) DCPythia-6.9B 在该数据集上的优势远大于 Pythia6.9B 在 Pile 和 Flan 上的表现。这可能得益于 DCMHA 在给定任务中动态组合现有头部的 QK 和 OV 电路的能力。附录 G 提供了对 DCPythia6.9B 如何解决该数据集中一个示例的机械解释分析和可视化。

表格 Table 5. 在合成数据集上的评估结果。

Figure 5. Pythia-6.9B 和 DCPythia-6.9B 的 QK 和 OV 头部的均值累积捕捉方差。

Head Diversity

在图5中，我们通过层叠 $W_{Q} W_{K}^{T}$ 和 $W_{O} W_{V}$ 矩阵，并计算它们主成分的累积捕获方差的均值，来测量 Pythia-6.9B 和 DCPythia6.9B 的头部多样性 (Cordonnier et al., 2020)。较低的数值表示层内注意力头的 $\mathrm{QK}$ 和 OV 电路具有更高的多样性。图5显示了 DCMHA 显著增强了 QK 电路的多样性，并适度提高了 OV 电路的多样性。头部多样性的提升也证明了 DCMHA 减少了头部冗余，提高了模型的表现能力。

由于 MHA 和 DCMHA 之间头部投影统计上的巨大差异，通过持续预训练将预训练的 Transformer 模型适应到 DCFormer 将会非常困难。我们在通过 Llama 架构从头开始在 $\mathrm{C} 4$ 数据集 (Raffel et al., 2020) 上预训练的 1.4B 模型上进行 1/10 步骤微调时，未能获得显著的改进。通过集成梯度归因分析，我们观察到低层头部组成比高层更为重要。另一方面，在微调预训练模型时，低层的梯度相对较小，阻碍了预训练模型中低层 MHA 的大幅更新，这与之前的观察结果一致 (如 Houlsby et al. (2019))。现有模型的适应困难也显示了 DCFormer 与 Transformer 之间的基本区别。

4.4. Training and Inference Overhead

由于 DCMHA 在 compose 函数中引入了额外的操作，我们在实际训练和推理环境中量化了其相对于 MHA 的开销。

尽管我们在大规模训练中使用了 Pythia 的架构，但本节的评估是在未训练的模型上进行的，这些模型使用的是 Transformer++/DCFormer++ 架构，因其性能更优秀而更具实际价值。我们测量了 4 种模型规模：2.8B 和 6.9B 模型是 Pythia 2.8B 和 6.9B 的 “LLaMAed” 版本；13B 和 33B 模型使用与 LLaMA 相同的架构 (Touvron et al. (2023), Table 2)。

我们在 TPU v3 pods 上训练，使用上下文长度为 2048、批次大小为 200 万令牌，测量 DCFormer 相对于 Transformer++ 的吞吐量和百分比。2.8B 和 6.9B 模型在 256 个 TPU v3 芯片上训练，而 13B 和 33B 模型在 512 个芯片上训练。在推理时，我们使用 A100 80G GPU，将提示长度和生成长度分别设置为 1024 和 128。我们使用批次大小为 1，测量生成 128 个令牌的速度。我们重复测量 3 次并取平均值。如前所述，所有 DCFormer++ 模型每隔一层使用一个局部注意窗口 256。除了与标准 Transformer++ 比较之外，我们还与相同注意窗口的 Transformer++ 进行比较，并报告第二个百分比作为比率。为了加速推理，我们将 Compose 的键级计算结果与 KVCache 一起缓存。这由于行加列分解 (Section 3.1) 是可行的，因为查询级和键级计算是独立的。此外，我们使用 torch.compile 加速 Transformer++ 和 DCFormer++。

表 6. Transformer++ 与 DCFormer++ 之间的训练吞吐量和推理速度比较。

如表6所示，训练开销通常比推理开销更大，且随模型规模增加而减少。这些开销虽然比表2中的理论估计要大并且不可忽视，但考虑到性能提升，尤其是在更大规模下，它们是可以接受的。开销主要是由于 Compose 引入的系列操作对注意矩阵的 I/O 瓶颈，而非计算瓶颈。目前，我们在纯 JAX 中实现训练，在纯 PyTorch 中实现推理，没有编写任何自定义核心。我们认为通过 FlashAttention 类似的平铺和核心融合技术 (Dao et al., 2022) 还有加速的空间，并将其留作未来工作。

4.5. Image Classification

除了仅限解码器的 transformer 或语言建模之外，我们还将 DCMHA 应用于视觉转换器 (ViT，一种仅限编码器的 transformer) (Dosovitskiy et al., 2020)，用于 Imagined-1k 数据集 (ILSVRC-2012) 的图像分类。实施和实验设置基于 Big Vision 代码库 $^{8}$ 。我们使用 ViT-S/16 作为基准模型，并配备 DCMHA 以获得 DCViT-S/16。我们还与一个 $1.7 x$ 更大的模型 ViT-M/16 进行比较（表7）。我们在表8中报告了 top-1 和 top-5 的准确率结果。DCViT-S/16 超过了 ViT-S/16，达到了与 ViT-M/16 相当的水平（尽管在第300次迭代时三者的准确率差异相对较小）。
Table 7. 用于 ImageNet-1k 分类的 ViT 模型架构。

4.6. 消融研究与权衡

我们对 DCMHA 的各种组件进行了消融和比较，重点关注在第 4.1 节中用于语言建模的 Transformer++/DCFormer++ 405M 模型的缩放法则实验设置（见表 3）。我们分别将每个（组）组件添加到 Transformer++ 中，以研究其效果，并在表 9 中报告困惑度结果。

表 8. 用于 ImageNet-1k 分类的 ViT 结果。

表 9. DCMHA 组件的消融。 $a =$ Talking-Heads Attention（Shazeer 等人，2020）； $b =$ all $- a =$ dyn. proj. + gate

动态 vs 静态虽然静态组合（静态投影，图 2 (b) 中的 Branch 1，也相当于 Talking-Heads Attention (Shazeer 等人，2020)）是有效的，但 DCFormer++ 使用的动态组合（dyn. proj. + gate）提高了很多，更接近 +all 配置，显示出动态性在增加表达能力中的关键作用。在动态组合组件中，低阶投影（Branch 2 和 4）比门控（Branch 3 和 5）更有效，这显示出了跨头共享的重要性。

查询为主 vs 键值为主当单独使用时，查询为主（Branch 2 和 3）和键值为主（Branch 4 和 5）的组合都表现得非常好，表明查询为主和键值为主的分支可以独立工作，之间很少交互，可能在其功能上有一些重叠。

预组合 vs 后组合单独使用时，后组合在注意力权重上的效果明显优于在注意力得分上的预组合，可能是因为注意力权重对 DCMHA 模块的最终输出有更直接的影响。这也揭示了只有考虑注意力得分组合的现有工作的不足之处（Wang et al., 2022; Nguyen et al., 2022; Cordonnier et al., 2020）。

秩的影响将动态投影秩 $R$ 从 1 增加到 2 时性能略有提升，但再次增加秩没有积极作用，验证了我们工作中选择 $R = 2$ 的合理性。

权衡我们探索了两种性能-效率权衡，可以进一步提高 DCMHA 的效率：1）增加局部:全局注意力层的比例，2）仅使用查询为主的组合。我们在不同规模上训练了两个模型（DCFormer++ 405M 和 DCPythia-6.9B），并通过衡量 Pile 验证困惑度来量化它们对性能的影响，如表 10 所示。对于 DCPythia-6.9B，我们只训练了 $\mathrm{~K}$ 步以节省计算成本。我们使用

表 10. 不同加速配置和模型的性能与速度权衡。（QW: Query-Wise，*：默认配置， $}^{\wedge}$ ：表 9 中的查询为主配置）

Transformer++/DCFormer++ 6.9B 在表 6 中研究了对训练和推理效率的影响。对于推理速度，我们将 DCFormer++6.9B 与两个 Transformer++6.9B 基线进行比较：一个具有全部全局注意力，另一个具有与 DCFormer++ 相同的局部:全局注意力比例。可以从表中看出，将局部:全局注意力比例从 1:1 增加到 7:1 提高了训练和推理效率，而不影响性能。仅使用查询为主的组合也提高了效率，而性能略有降低。这两种方法也可以结合使用，提供一系列权衡。具体来说，将 3:1 局部:全局注意力与查询为主的组合结合，提高了 DCFormer++ 6.9B 的训练吞吐量比例从 $\%$ 到 $\%$ ，提高了推理速度比例从 $\% / 88.7 \%$ 到 $\% / 93.5 \%$ ，虽然困惑度比默认的 DCFormer 略差，但仍显著优于 Transformer 基线。

5. 结论

我们引入了一种动态头部组合机制，以改进变压器的 MHA 模块。实验结果表明，DCFormer 是有效的，高效且可扩展的，在基础模型的重要语言建模任务上显著优于强大的变压器基线。未来，我们希望将动态头部组合的理念应用于更多的架构和领域，并进行更多关于 DCMHA 的可解释性研究，以深入了解其工作机制。

影响声明

这篇论文介绍了一种通过动态组合多头注意力机制来改进 Transformer 架构的方法，该方法可以在增加很少开销的情况下提升大型语言模型的性能。在实际应用中，这一方法可以帮助节省预训练成本并减少碳足迹，尤其是在大型语言模型（LLMs）时代。此外，我们的开源代码和模型可以推进架构创新的研究，并促进大型语言模型的下游应用。然而，也存在模型被恶意利用生成有害内容的可能性，这可能会对社会产生负面影响。