Eigen库使用

前言

Eigen是一个高层次的C ++库，有效支持 得到的线性代数，矩阵和矢量运算，数值分析及其相关的算法。

配置

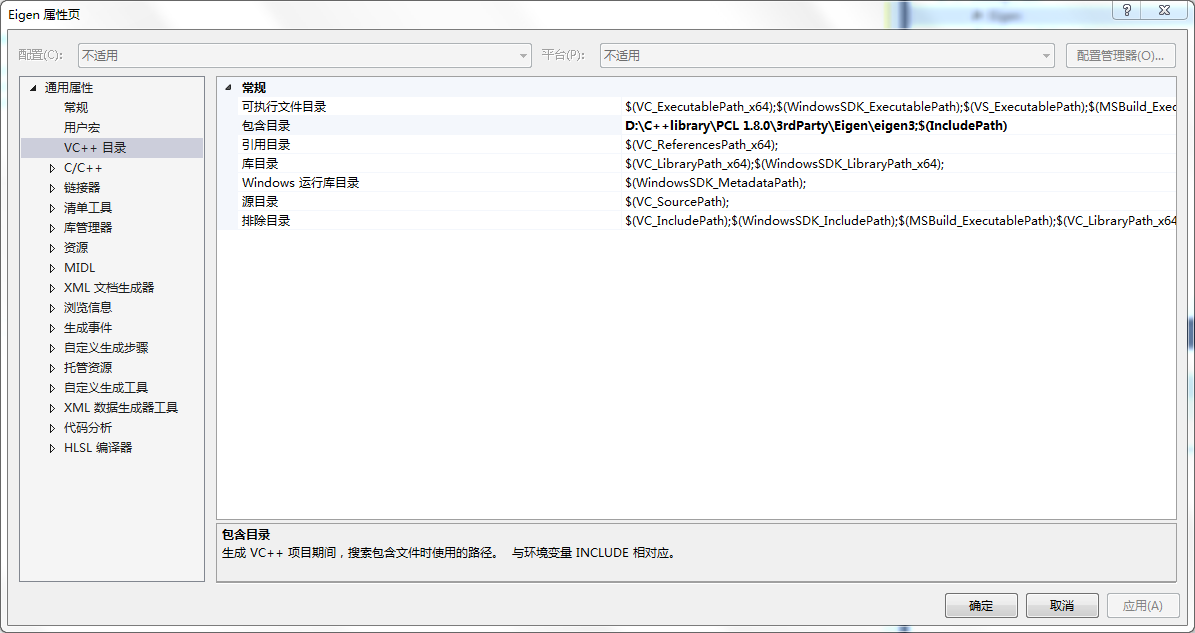
关于Eigen库的配置只需要在属性表包含目录中添加Eigen路径即可。

例子

Example 1：

#include <iostream>
#include <Eigen/Dense>

void main()
{
    Eigen::MatrixXd m(2, 2);            //声明一个MatrixXd类型的变量，它是2*2的矩阵，未初始化
    m(0, 0) = 3;                        //将矩阵第1个元素初始化3
    m(1, 0) = 2.5;                      //将矩阵第3个元素初始化3
    m(0, 1) = -1;  
    m(1, 1) = m(1, 0) + m(0, 1);  
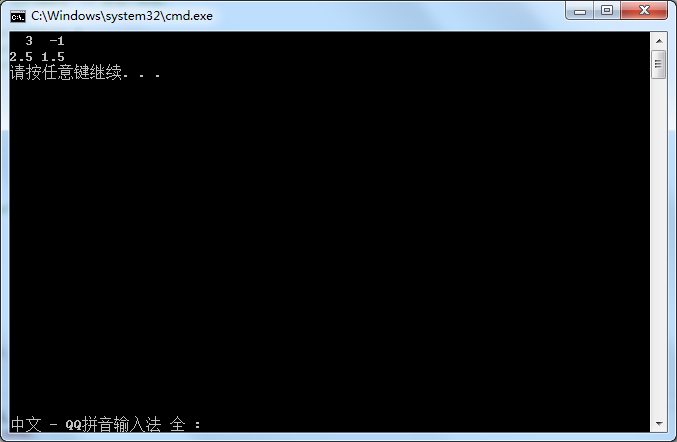
    std::cout << m << std::endl;
}

Eigen头文件定义了很多类型，但对于简单的应用程序，可能只使用MatrixXd类型。 这表示任意大小的矩阵（MatrixXd中的X），其中每个条目是双精度（MatrixXd中的d）。 Eigen / Dense头文件定义了MatrixXd类型和相关类型的所有成员函数。 在这个头文件中定义的所有类和函数都在特征名称空间中。

Example 2：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main()
{  
    MatrixXd m = MatrixXd::Random(3,3);                 //使用Random随机初始化3*3的矩阵
    m = (m + MatrixXd::Constant(3,3,1.2)) * 50;  
    cout << "m =" << endl << m << endl;  
    VectorXd v(3);                                      //这表示任意大小的（列）向量。
    v << 1, 2, 3;  
    cout << "m * v =" << endl << m * v << endl;
}

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main()
{  
    Matrix3d m = Matrix3d::Random();                    //使用Random随机初始化固定大小的3*3的矩阵
    m = (m + Matrix3d::Constant(1.2)) * 50;  
    cout << "m =" << endl << m << endl;  Vector3d v(1,2,3);    
    cout << "m * v =" << endl << m * v << endl;
}

Matrix&Vector

Example 3：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{  
    MatrixXd m(2,2);  
    m(0,0) = 3;  
    m(1,0) = 2.5;  
    m(0,1) = -1;  
    m(1,1) = m(1,0) + m(0,1);  
    std::cout << "Here is the matrix m:\n" << m << std::endl;  
    VectorXd v(2);  
    v(0) = 4;  
    v(1) = v(0) - 1;  
    std::cout << "Here is the vector v:\n" << v << std::endl;
}

逗号初始化

Example 4：

Matrix3f m;
m << 1, 2, 3,     4, 5, 6,     7, 8, 9;
std::cout << m;

通过Resize调整矩阵大小

矩阵的当前大小可以通过rows（），cols（）和size（）检索。 这些方法分别返回行数，列数和系数数。 通过resize（）方法调整动态大小矩阵的大小。
Example 5：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{  
    MatrixXd m(2,5);                //初始化大小2*5
    m.resize(4,3);                  //重新调整为4*3
    std::cout << "The matrix m is of size "            << m.rows() << "x" << m.cols() << std::endl;  
    std::cout << "It has " << m.size() << " coefficients" << std::endl;  
    VectorXd v(2);  v.resize(5);  
    std::cout << "The vector v is of size " << v.size() << std::endl;
    std::cout << "As a matrix, v is of size "            << v.rows() << "x" << v.cols() << std::endl;
}

通过赋值调整矩阵大小

Example 6：

MatrixXf a(2, 2); 
std::cout << "a is of size " << a.rows() << "x" << a.cols() << std::endl; 
MatrixXf b(3, 3); 
a = b; 
std::cout << "a is now of size " << a.rows() << "x" << a.cols() << std::endl;

Eigen + - * 等运算

Eigen通过通用的C ++算术运算符（例如+， - ，）或通过特殊方法（如dot（），cross（）等）的重载提供矩阵/向量算术运算。对于Matrix类（矩阵和向量） 只被重载以支持线性代数运算。 例如，matrix1 matrix2表示矩阵矩阵乘积。
Example 7：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{  
    Matrix2d a;  a << 1, 2,       3, 4;  
    MatrixXd b(2,2); 
    b << 2, 3,       1, 4; 
    std::cout << "a + b =\n" << a + b << std::endl;
    std::cout << "a - b =\n" << a - b << std::endl; 
    std::cout << "Doing a += b;" << std::endl; 
    a += b;  
    std::cout << "Now a =\n" << a << std::endl; 
    Vector3d v(1,2,3);  
    Vector3d w(1,0,0);  
    std::cout << "-v + w - v =\n" << -v + w - v << std::endl;
}

Example 8：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{  
    Matrix2d a;  
    a << 1, 2,       3, 4;  
    Vector3d v(1,2,3);  
    std::cout << "a * 2.5 =\n" << a * 2.5 << std::endl; 
    std::cout << "0.1 * v =\n" << 0.1 * v << std::endl; 
    std::cout << "Doing v *= 2;" << std::endl;  v *= 2; 
    std::cout << "Now v =\n" << v << std::endl;
}

矩阵转置、共轭和伴随矩阵

MatrixXcf a = MatrixXcf::Random(2,2);
cout << "Here is the matrix a\n" << a << endl;
cout << "Here is the matrix a^T\n" << a.transpose() << endl;
cout << "Here is the conjugate of a\n" << a.conjugate() << endl;
cout << "Here is the matrix a^*\n" << a.adjoint() << endl;

禁止如下操作：

a = a.transpose(); // !!! do NOT do this !!!

但是可以使用如下函数：

a.transposeInPlace();

此时a被其转置替换。

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{
    Matrix2i a;
    a << 1, 2, 3, 4;
    std::cout << "Here is the matrix a:\n" << a << std::endl;
    a = a.transpose(); // !!! do NOT do this !!!
    std::cout << "and the result of the aliasing effect:\n" << a << std::endl;
}

矩阵* 矩阵和矩阵* 向量操作

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
int main()
{  
    Matrix2d mat;  mat << 1, 2,         3, 4;  
    Vector2d u(-1,1), v(2,0);  
    std::cout << "Here is mat*mat:\n" << mat*mat << std::endl;  
    std::cout << "Here is mat*u:\n" << mat*u << std::endl;  
    std::cout << "Here is u^T*mat:\n" << u.transpose()*mat << std::endl; 
    std::cout << "Here is u^T*v:\n" << u.transpose()*v << std::endl;
    std::cout << "Here is u*v^T:\n" << u*v.transpose() << std::endl;  
    std::cout << "Let's multiply mat by itself" << std::endl;  
    mat = mat*mat;  std::cout << "Now mat is mat:\n" << mat << std::endl;
}

点乘和叉乘

对于点积和叉乘积，需要使用dot（）和cross（）方法。

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
int main()
{  
    Vector3d v(1,2,3);  
    Vector3d w(0,1,2); 
    cout << "Dot product: " << v.dot(w) << endl; 
    double dp = v.adjoint()*w; // automatic conversion of the inner product to a scalar  
    cout << "Dot product via a matrix product: " << dp << endl;  
    cout << "Cross product:\n" << v.cross(w) << endl;
}

#include <iostream>
#include <Eigen/Dense>
using namespace std;
int main()
{  
    Eigen::Matrix2d mat;
    mat << 1, 2,         3, 4;
    cout << "Here is mat.sum():       " << mat.sum()       << endl;  
    cout << "Here is mat.prod():      " << mat.prod()      << endl; 
    cout << "Here is mat.mean():      " << mat.mean()      << endl; 
    cout << "Here is mat.minCoeff():  " << mat.minCoeff()  << endl;  
    cout << "Here is mat.maxCoeff():  " << mat.maxCoeff()  << endl; 
    cout << "Here is mat.trace():     " << mat.trace()     << endl;
}

数组的运算（未完待续）

Eigen最小二乘估计

最小平方求解的最好方法是使用SVD分解。 Eigen提供一个作为JacobiSVD类，它的solve（）是做最小二乘解。式子为Ax=b
经过和Matlab对比。

#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{   
    MatrixXf A = MatrixXf::Random(3, 2);  
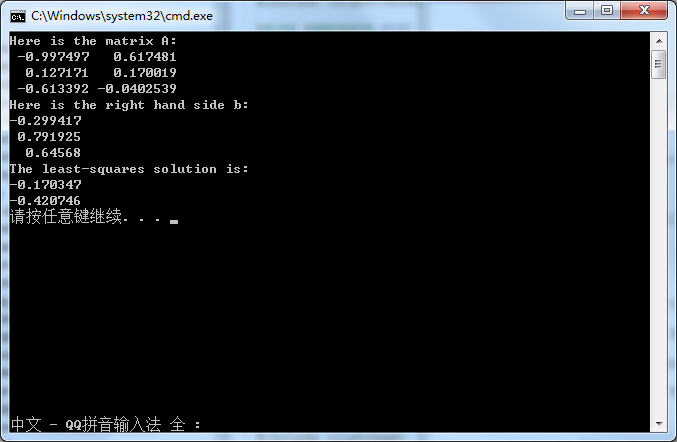
    cout << "Here is the matrix A:\n" << A << endl;  
    VectorXf b = VectorXf::Random(3);   
    cout << "Here is the right hand side b:\n" << b << endl;  
    cout << "The least-squares solution is:\n"        << A.jacobiSvd(ComputeThinU | ComputeThinV).solve(b) << endl;
}