散射需要:吸收,内散射,外散射
分为瑞利散射Rayleigh Scattering和米氏散射 Mie Scattering 后面会详细讲解
大气中散射由多种原因产生,微粒,尘埃,水蒸气等等
阳光由于散射增加会减弱并变色

物体也会随着距离增加散射增加而减弱并变色

大气光线散射由于 一天中的时间,天气,污染的改变而改变
辐射通量Radiant Flux
辐射率Radiance
辐照度Irradiance
辐射通量Φ (Radiant Flux)
代表通过表面的光照量,辐射强度 (能量/时间),单位:瓦特
辐射率L (Radiance)
代表一束光线的光照量,辐射通量/面积/立体角,单位:瓦特/(m²*球面角度 )
吸收截面积σab (Absorption cross section)
每辐照度的吸收辐射通量Φ/E,单位:面积(m²)
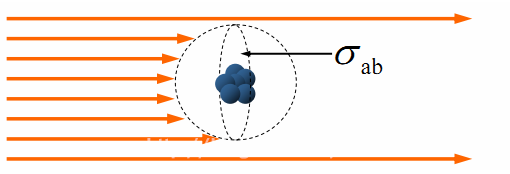
之间关系:
Φ = E*σab
σab = Φ/ E
吸收系数 βab (Absorption coefficient)
代表粒子密度 ρab Particle density, 单位:逆长度(m-1)
总吸收截面积:
Aab = σab * ρab * A *ds
A:介质总面积,ds:介质厚度
吸收的概率:
Pab = Aab/A =σab * ρab * ds = βab
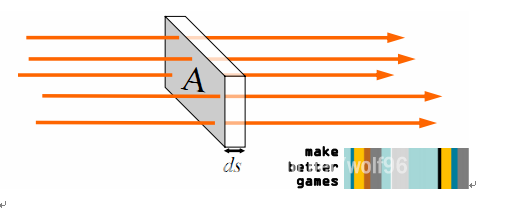
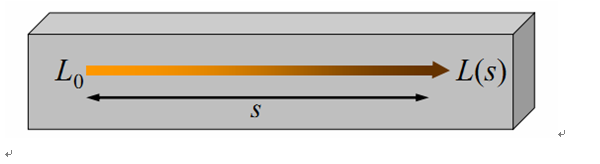
光辐射经过固定密度的吸收介质的衰减:
L(s) = L0e-βab*s
s:介质厚度距离
散射粒子密度ρsc
散射系数βsc βsc =ρsc * σsc
由于在固定密度的介质的外反射造成的衰减:L(s) = L0e-βsc*s
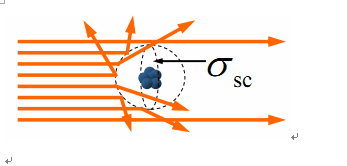
消光 Extinction
吸收与外散射损失的光线就是消光 Extinction
消光系数 Extinction coefficient βex = βab + βsc
消光产生的总衰减L(s) = L0e-βex*s --> Fex(s) = e-βex*s
散射相函数f(θ, ϕ)
大多数大气粒子是球形的或非常小 f(θ, ϕ) = f(θ)
f(θ)的用途:
内散射概率:f(θ)* ωsun In-scatter probability
内散射辐射率:f(θ)* ωsun*Lsun = f(θ)* Esun
θ为light方向与view方向的夹角
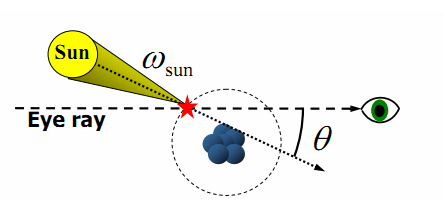
在同一个路径(path)中的的内散射
一次事件的辐射率: f(θ)* Esun
在同一个散射距离ds: f(θ)* Esun*βsc*ds
角散射
角散射系数 Angular scattering coefficient βsc(θ) = βsc*f(θ)
经过ds距离的内散射:Esun*βsc(θ)*ds
βsc(θ)的单位:m-1* steradian-1
增加太阳光穿过固定密度的散射媒介的辐射率
Lin(s, θ) = 1/βex * Esun * βsc(θ)*(1- e-βex*s)
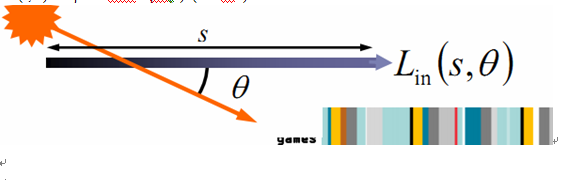
对比GPU 雾渲染
L (s, θ) = L0(1-f(s)) +Cfog*f(s)
单纯的权重运算,效果不好
相函数:
fr(θ) = 3/(16 *π)*(1+cos²θ)

瑞利散射是米氏散射的一种
当光线穿过大气层,大气中气体蓝色部分瑞利散射强烈,但是红色或黄色等波长长的瑞利散射很弱。
由于天空产生的蓝色的光的散射,阳光到地面的颜色发黄。在日出日落中, 由于空气密度的增加和地球表面附近的粒子,瑞利散射效应更明显。
相比之下,水滴组成云与可见光的波长大小类似,更倾向于米氏散射而非瑞利散射。假设所有可见光的波长分布大致相同,因此云看起来是是白色或灰色的。
在多云天气主要是米氏散射(水滴)
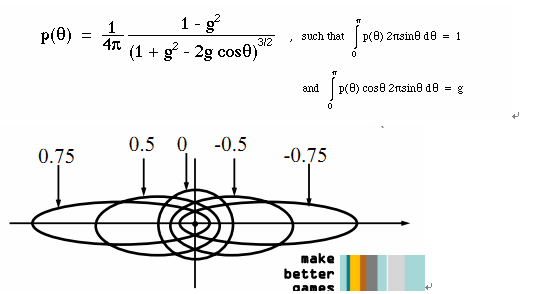
fHG(θ) = (1-g) 2/(4*π* (1+g2-2g*cos (θ)))3/2
g为各向异性因子anisotropy factor
现实中,空气经常包含各种各样大小的米氏粒子Mie particles的混合,总的来说任何波长相关性倾向于平均
通常情况下,光线被吸收是轻微的
βex = βscRayleigh +βscMie
总结与实现
shader中:
传入参数:
βscRayleigh
βscMie
gHG
常量:
E0sun
Esun收到消光extinction影响所以不是常量
阳光能量传到地面上会有衰减
实现结果
分为瑞利散射Rayleigh Scattering和米氏散射 Mie Scattering 后面会详细讲解
大气中散射由多种原因产生,微粒,尘埃,水蒸气等等
阳光由于散射增加会减弱并变色

物体也会随着距离增加散射增加而减弱并变色

大气光线散射由于 一天中的时间,天气,污染的改变而改变
散射共通篇
Radiometric Quantities辐射度量包括:辐射通量Radiant Flux
辐射率Radiance
辐照度Irradiance
辐射通量Φ (Radiant Flux)
代表通过表面的光照量,辐射强度 (能量/时间),单位:瓦特
辐射率L (Radiance)
代表一束光线的光照量,辐射通量/面积/立体角,单位:瓦特/(m²*球面角度 )
辐照度E
代表到表面上一个点的光照量,入射辐射通量/面积(瓦特/m²),辐射集中成半球状
吸收截面积σab (Absorption cross section)
每辐照度的吸收辐射通量Φ/E,单位:面积(m²)

之间关系:
Φ = E*σab
σab = Φ/ E
吸收系数 βab (Absorption coefficient)
代表粒子密度 ρab Particle density, 单位:逆长度(m-1)
总吸收截面积:
Aab = σab * ρab * A *ds
A:介质总面积,ds:介质厚度
吸收的概率:
Pab = Aab/A =σab * ρab * ds = βab

光辐射经过固定密度的吸收介质的衰减:
L(s) = L0e-βab*s
s:介质厚度距离

外散射
散射截面σsc Scattering cross section散射粒子密度ρsc
散射系数βsc βsc =ρsc * σsc
由于在固定密度的介质的外反射造成的衰减:L(s) = L0e-βsc*s

消光 Extinction
吸收与外散射损失的光线就是消光 Extinction
消光系数 Extinction coefficient βex = βab + βsc
消光产生的总衰减L(s) = L0e-βex*s --> Fex(s) = e-βex*s
内散射
所有方向的光在视角方向的散射,来自太阳,天空,大地,我们只需要处理来自太阳的内散射即可散射相函数f(θ, ϕ)
大多数大气粒子是球形的或非常小 f(θ, ϕ) = f(θ)
f(θ)的用途:
内散射概率:f(θ)* ωsun In-scatter probability
内散射辐射率:f(θ)* ωsun*Lsun = f(θ)* Esun
θ为light方向与view方向的夹角

在同一个路径(path)中的的内散射
一次事件的辐射率: f(θ)* Esun
在同一个散射距离ds: f(θ)* Esun*βsc*ds
角散射
角散射系数 Angular scattering coefficient βsc(θ) = βsc*f(θ)
经过ds距离的内散射:Esun*βsc(θ)*ds
βsc(θ)的单位:m-1* steradian-1
增加太阳光穿过固定密度的散射媒介的辐射率
Lin(s, θ) = 1/βex * Esun * βsc(θ)*(1- e-βex*s)

消光与内散射
L (s, θ) = L0Fex(s) +Lin(s, θ)对比GPU 雾渲染
L (s, θ) = L0(1-f(s)) +Cfog*f(s)
单纯的权重运算,效果不好
瑞利散射 Rayleigh Scattering
粒子微小(r<0.05 λ)相函数:
fr(θ) = 3/(16 *π)*(1+cos²θ)

瑞利散射是米氏散射的一种
当光线穿过大气层,大气中气体蓝色部分瑞利散射强烈,但是红色或黄色等波长长的瑞利散射很弱。
由于天空产生的蓝色的光的散射,阳光到地面的颜色发黄。在日出日落中, 由于空气密度的增加和地球表面附近的粒子,瑞利散射效应更明显。
相比之下,水滴组成云与可见光的波长大小类似,更倾向于米氏散射而非瑞利散射。假设所有可见光的波长分布大致相同,因此云看起来是是白色或灰色的。
米氏散射 Mie Scattering
烟雾和云散射牛奶、生物组织和乳胶漆之类大粒子在多云天气主要是米氏散射(水滴)
发生米氏散射的介质中粒子大,为球形粒子
fHG(θ) = (1-g) 2/(4*π* (1+g2-2g*cos (θ)))3/2
g为各向异性因子anisotropy factor
现实中,空气经常包含各种各样大小的米氏粒子Mie particles的混合,总的来说任何波长相关性倾向于平均
混合散射
现实中,空气中瑞利散射和米氏散射都有通常情况下,光线被吸收是轻微的
βex = βscRayleigh +βscMie
总结与实现
shader中:传入参数:
βscRayleigh
βscMie
gHG
常量:
E0sun
Esun收到消光extinction影响所以不是常量
阳光能量传到地面上会有衰减
注意:
起点处最初的阳光是白色的
密度不是常量
实现所需的所有公式:
关键部分实现代码:
<span style="font-size:14px;">float s = (GetDepth(i.uv_MainTex)-0.8)*5;
float Fex = pow(e, -(_Beta_R + _Beta_M)* s);
float beta_r = 3 / (16 * PIE)*_Beta_R*(1 + cos_theta* cos_theta);
float beta_m = 1 / (4 * PIE) * _Beta_M * (1 - _G)*(1 - _G) / pow((1 + _G * _G - 2 * _G*cos_theta), 3 / 2);
float3 Lin = (beta_r + beta_m) / (_Beta_R + _Beta_M)* _Sun * (1 - pow(e, -(_Beta_R + _Beta_M)* s));
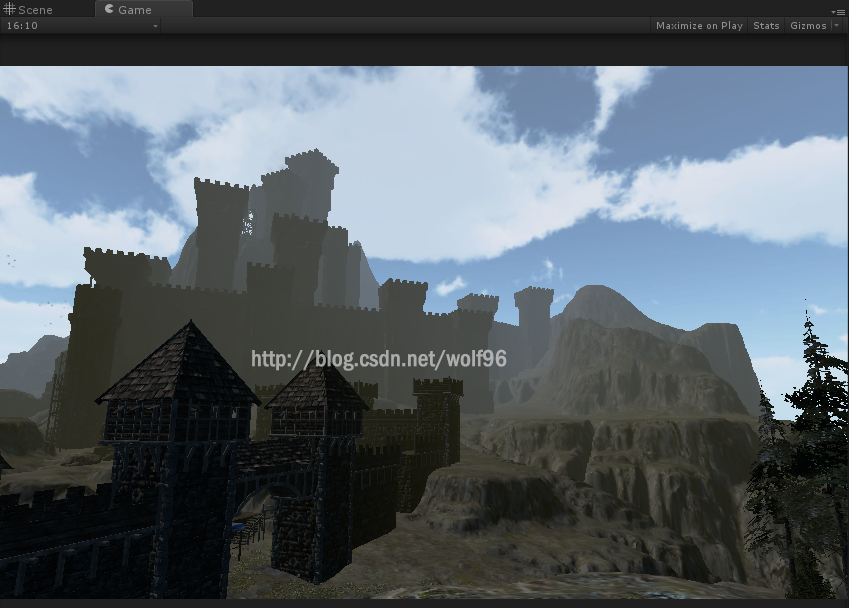
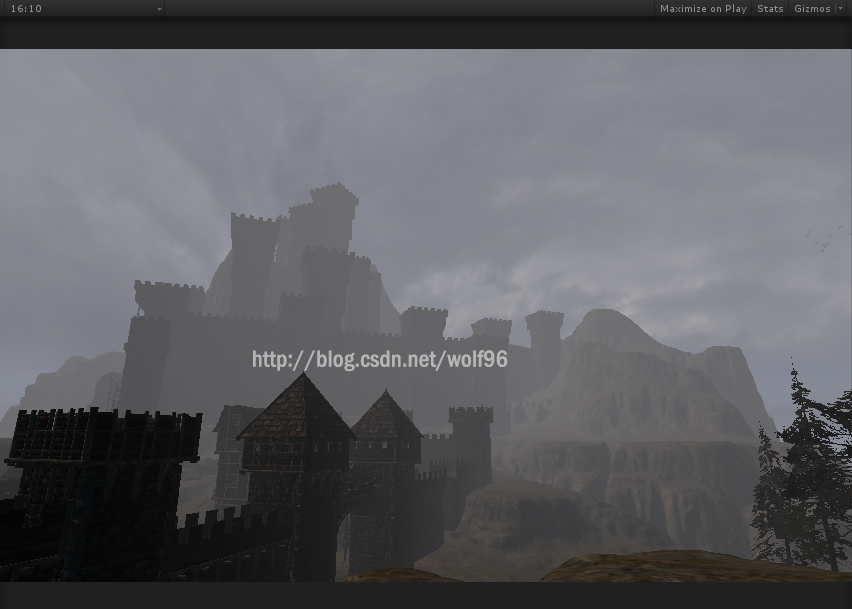
float3 L = _Sun * Fex + color.rgb *Lin;</span>实现结果
瑞利散射
米氏散射
混合散射
参考:Rendering Outdoor Light Scattering in Real Time











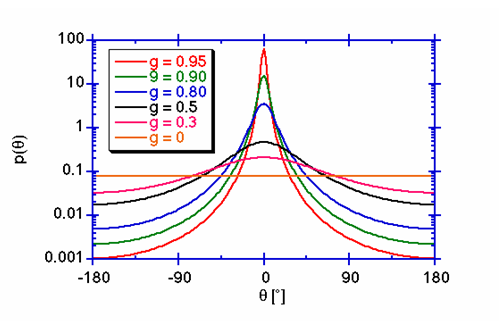

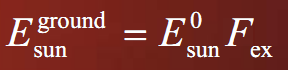

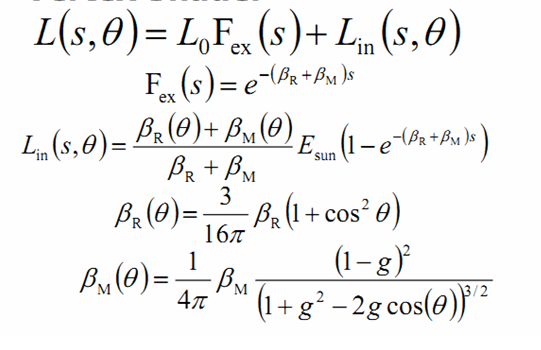














 275
275

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








