OFDM接收原理

1.基本的接收模型

$$y_n=\sum _{t=0}^{N-1}{h}_n(t)\cdot x_{n-t}+n_n$$又我们有
$$x_n=\frac{1}{\sqrt{N}}\sum _{k=1}^K{X}_k{e}^{\frac{j2\pi nk}{N}},x_{n-t}=\frac{1}{\sqrt{N}}\sum _{k=1}^K{X}_k{e}^{\frac{j2\pi nk}{N}}{e}^{-\frac{j2\pi tk}{N}}$$将$x_{n-t}$代入，可得
$$y_n=\frac{1}{\sqrt{N}}\sum _{t=0}^{N-1}{h}_n(t)\cdot \sum _{k=1}^K{X}_k{e}^{\frac{j2\pi nk}{N}}{e}^{-\frac{j2\pi tk}{N}}+n_n$$对上式进行重写,即对$h(n)$进行傅里叶变换
$$y_n=\frac{1}{\sqrt{N}}\cdot \sum _{k=1}^N{X}_k{H}_n(k)e^{\frac{j2\pi nk}{N}}+n_n$$再对$y_n$进行傅里叶变换可以得到
$$Y_k=\frac{1}{\sqrt{N}}\sum _{k=1}^K{y}_n{e}^{-\frac{j2\pi nk}{N}}$$再将$y_n$代入可得
$$Y=H\cdot X+n$$其中，列向量定义如下：
$$Y=\left[\begin{array}{c}{Y}_0\\ ⋮\\ Y_{N-1}\end{array}\right],X=\left[\begin{array}{c}{X}_0\\ ⋮\\ Y_{N-1}\end{array}\right],h=\left[\begin{array}{c}{H}_0\\ ⋮\\ H_{N-1}\end{array}\right]$$
如果信道是时不变的，那么给定的信道矩阵为对角阵。
并行信道表示如下图所示：

就像平常的信道一样。

2.循环卷积

我们假设有两个信道$h1,h2$，OFDM的图如下图所示：

信息的传输如下图所示：

这是有循环前缀的情况，若是去掉循环前缀，那么我们可以得到矩阵：$$Y=\overline{H}X$$

为什么H矩阵的第一项会是如上图所示的那样呢？
因为从未去掉循环前缀的矩阵中我们可以得到第三项，也就是去除循环前缀的第一项，是$$y_2=h_2{x}_6+h_1{x}_1$$去掉后，我们的信道矩阵第一项就得在最后加上$h_2$这一条了。

• 加入CP和去除cp，将线性卷积变为循环卷积
• 这将为我们处理信道矩阵带来巨大的便捷

3.信道的特征向量

• 一个循环矩阵可以通过DFT实现对角化，也就是说，循环矩阵的特征值和DFT相同，而循环矩阵的特征向量都是线性独立的。
• 令G代表一个$NXN$的循环矩阵

循环矩阵的特征值如下：$$\lambda =\sum _{p=0}^{N-1}g(p)\cdot e^{j\frac{2\pi }{N}kp}$$
特征值对应的向量为：

再用SVD的方法来对角化信道，得到比较好的信道性能。有$$y=\overline{H}x$$
将其对角化，得到$$y=W\cdot D\cdot W^{\ast }\cdot x$$
两边同乘$w^{-1}$,得到$$W^{-1}y=D\cdot W^{\ast }\cdot x$$
等式左边代表接收信号的傅里叶变换，右边代表经过对角阵特征值加权后的数据符号的傅里叶反变换。

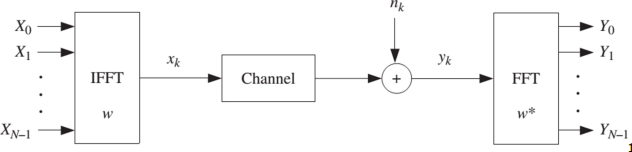
4.OFDM的优缺点

4.1优点

• 抗多径衰落能力强。
• 对于频率选择性衰落信道，OFDM可以通过子载波的动态比特分配，自适应功率分配和调制方式的改变，达到最大的信道容量
• 易于实现

4.2缺点

• 由于频谱相互重叠，所以OFDM对于频率的正交性要求很严格，因此对于传输过程中的频偏要求十分敏感，大约1/100的频偏才是可以被接受的。
• 峰值功率与平均功率之比（PAPR）很大，原理上，这将增加成本。
• 容易发生多载波互调失真，因此要求整个信号发送过程中线性很好。