一、背景
Calibration是机器人开发者永远的痛。虽然说方法说起来几十年前就有,但每一个要用摄像头的人都还是要经过一番痛苦的踩坑,没有轻轻松松拿来就效果好的包。其实人类不就是个手眼协调的先进“机器人”吗,O(∩_∩)O哈哈~

机器人视觉应用中,手眼标定是一个非常基础且关键的问题。简单来说手眼标定的目的就是获取机器人坐标系和相机坐标系的关系,最后将视觉识别的结果转移到机器人坐标系下。
手眼标定行业内分为两种形式,根据相机固定的地方不同,如果相机和机器人末端固定在一起,就称之为“眼在手”(eye in hand),如果相机固定在机器人外面的底座上,则称之为“眼在外”(eye to hand)。

眼在外

眼在手
二、手眼关系的数学描述
1. eye in hand,这种关系下,两次运动,机器人底座和标定板的关系始终不变。求解的量为相机和机器人末端坐标系的位姿关系。

2. eye to hand,这种关系下,两次运动,机器人末端和标定板的位姿关系始终不变。求解的量为相机和机器人底座坐标系之间的位姿关系。

手眼标定eye in hand 和eye to hand 的区别主要是机器人那边。一个是end相对于base,另一个是base相对于end。千万注意,对于eye to hand 这种模式,机器人的位置、姿态是末端相对于底座的信息,并非示教器上的读数。

三、AX = XB问题的求解
旋转和平移分步法求解:
- Y. Shiu, S. Ahmad Calibration of Wrist-Mounted Robotic Sensors by Solving Homogeneous Transform Equations of the Form AX = XB. In IEEE Transactions on Robotics and Automation, 5(1):16-29, 1989.
- R. Tsai, R. Lenz A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration. In IEEE Transactions on Robotics and Automation, 5(3):345-358, 1989.
迭代求解及相关资料可以看看相关网上的英文教程 Calibration and Registration Techniques for Robotics其中也有一些AX= XB的matlab代码可以使用。
ROS 下也有相关的一些package可以利用
GitHub - IFL-CAMP/easy_handeye: Automated, hardware-independent Hand-Eye Calibration
Visual Servoing Platform: Tutorial: Camera extrinsic calibration
HandEyeCalibration TUM这里也有很多手眼标定求解的参考链接
四、其他参考资料
3D 视觉之手眼标定 邱强Flyqq 微信文章
手眼标定的两种方式_wzj5530的专栏-CSDN博客_手眼标定 图不错
深入浅出地理解机器人手眼标定_二毛的博客-CSDN博客_机器人手眼标定 部分halcon代码
eye-in-hand手眼标定系统_二毛的博客-CSDN博客 halcon代码
手眼标定之9点法_GoRunningSnail的博客-CSDN博客 部分原理
UR5、Kinect2手眼标定总结_zhang970187013的博客-CSDN博客 UR5 与easy hand eye
一般用“两步法”求解基本方程,即先从基本方程上式求解出旋转部分,再代入求解出平移部分。
经典手眼标定算法之Tsai-Lenz的OpenCV实现_YunlinWang的博客-CSDN博客
============== Halcon 官方示例-手眼标定 ==================

五、Matlab下手眼标定解算
相机与机器人是eye-to-hand模式,机器人为加拿大Kinova 6轴机械臂,机器人pose为基座相对于末端的x,y,z,qx,qy,qz,qw, 单位为米。姿态使用单位四元数表示。
2017.08.29Kinova_pose_all_8_1.txt
0.4285232296,0.1977596461,-0.5595823047,0.4738016082,0.3209333657,-0.2268795901,-0.7880605703
0.2265712272,0.0261943502,-0.6661910850,0.5222343809,0.0461668455,-0.1315038186,-0.8413362107
0.1058885008,0.0527681997,-0.7419267756,0.5081638565,-0.0263721340,-0.1696570449,-0.8439730402
0.1127224767,-0.0420359377,-0.7413071786,0.5101706595,-0.0322252464,-0.1864402870,-0.8390038445
0.2592932751,-0.0329068529,-0.7162865014,0.5101641882,0.1265739325,-0.0153077050,-0.8505746380
-0.1724239544,0.0084144761,-0.6998332592,0.4989369998,-0.0973210400,-0.1244194561,-0.8521210503
-0.0534271258,0.0771779706,-0.6845820453,0.5195499916,0.0511217081,-0.1691595167,-0.8359661686
0.2598500029,0.0933230213,-0.6638257382,0.5673912325,0.1686973705,-0.1427337629,-0.7932436318pattern pose为标定板相对于相机的x,y,z,qx,qy,qz,qw, 单位为米。姿态使用单位四元数表示。
2017.08.29Pattern_pose_all_8_1.txt
0.4277459616,-0.0267754900,0.0822384718,0.3555198802,-0.2313832954,-0.6738796808,-0.6049409568
0.4610891450,-0.0089776615,0.0394863697,-0.4168581229,0.4389318994,0.4953132086,0.6230833961
0.4159190432,0.0112235849,0.0112504715,-0.3559197420,0.4898053987,0.4542453721,0.6535081871
0.4143974465,0.0094036803,0.1073298638,-0.3438949365,0.4875942762,0.4507613906,0.6639294113
0.3473267442,-0.1866610227,0.0651366494,0.4966101920,-0.4291949558,-0.5361047392,-0.5308123169
0.3883165305,-0.2249779584,0.0093256602,-0.3595692001,0.5529429756,0.4090559739,0.6305848604
0.4309364801,-0.2354261800,-0.0925819097,-0.3831460128,0.4244707870,0.5043032275,0.6470718186
0.4362292324,-0.0778107597,-0.1007970399,0.4568889439,-0.3144470665,-0.5302104578,-0.6412896427
此Matlab文件调用数据进行离线解算。Calibration and Registration Techniques for Robotics 的这部分Registering Two Sets of 6DoF Data with 1 Unknown,有code下载,下载好命名为shiu.m和tsai.m供下面程序调用就行。我这里贴出
tsai.m
function X = tsai_wechat(A,B)
% Calculates the least squares solution of
% AX = XB
%
% A New Technique for Fully Autonomous
% and Efficient 3D Robotics Hand/Eye Calibration
% Lenz Tsai
%
% Mili Shah
% July 2014
[m,n] = size(A); n = n/4;
S = zeros(3*n,3);
v = zeros(3*n,1);
%Calculate best rotation R
for i = 1:n
A1 = logm(A(1:3,4*i-3:4*i-1));
B1 = logm(B(1:3,4*i-3:4*i-1));
a = [A1(3,2) A1(1,3) A1(2,1)]'; a = a/norm(a);
b = [B1(3,2) B1(1,3) B1(2,1)]'; b = b/norm(b);
S(3*i-2:3*i,:) = skew(a+b);
v(3*i-2:3*i,:) = a-b;
end
x = S\v;
theta = 2*atan(norm(x));
x = x/norm(x);
R = (eye(3)*cos(theta) + sin(theta)*skew(x) + (1-cos(theta))*x*x')';
%Calculate best translation t
C = zeros(3*n,3);
d = zeros(3*n,1);
I = eye(3);
for i = 1:n
C(3*i-2:3*i,:) = I - A(1:3,4*i-3:4*i-1);
d(3*i-2:3*i,:) = A(1:3,4*i)-R*B(1:3,4*i);
end
t = C\d;
%Put everything together to form X
X = [R t;0 0 0 1];Jaco_handeye_test_10.m 测试程序中用到了Peter Corke老师的机器人工具箱。我的Matlab版本R2013a,利用机器人工具箱的一些转换函数(四元数的构建,欧拉角转换等),它安装和基本使用参考这里:Matlab机器人工具箱_Learning by doing-CSDN博客_matlab机器人工具箱
clear;
close all;
clc;
% Robot pose in Quatenion xyzw
JacoCartesianPose = importdata('E:\\Matlab_work\\handeye\\yake_handeye\\2017.08.29Kinova_pose_all_8_1.txt');
[m,n] = size(JacoCartesianPose); % 8* 7
A = cell(1,m); % 1*8
for i = 1: m
robotHtool_qua = Quaternion([ JacoCartesianPose(i, 7), JacoCartesianPose(i, 4), JacoCartesianPose(i, 5) , JacoCartesianPose(i, 6)]) ;
A{1,i} = transl(JacoCartesianPose(i, 1), JacoCartesianPose(i, 2), JacoCartesianPose(i, 3)) * robotHtool_qua.T;
end
% Pattern Pose(Homogeneous) stored in cell B.
patternInCamPose = importdata('E:\\Matlab_work\\handeye\\yake_handeye\\2017.08.29Pattern_pose_all_8_1.txt');
[melem,nelem] = size(patternInCamPose); % 8*7
B=cell(1,melem);
for x=1: melem
camHmarker_qua = Quaternion([ patternInCamPose(x, 7) , patternInCamPose(x, 4), patternInCamPose(x, 5) , patternInCamPose(x, 6)]) ;
B{1,x} = transl(patternInCamPose(x, 1), patternInCamPose(x, 2), patternInCamPose(x, 3)) * camHmarker_qua.T;
end
%
n2=m;
TA=cell(1,n2);
TB=cell(1,n2);
%--------------------- 8 -----------------------------------
M1=[];
M2=[];
for j=[1: m-1]% 1-7.
TA{1, j} = inv(A{1, j}) * A{1, j+1};
M1=[M1 TA{1, j}];
TB{1, j} = B{1, j} * inv(B{1, j+1});
M2=[M2 TB{1, j}];
end
% M1=[TA{1,1} TA{1,2} TA{1,3} TA{1,4} TA{1,5} TA{1,6} TA{1,7} ];
% M2=[TB{1,1} TB{1,2} TB{1,3} TB{1,4} TB{1,5} TB{1,6} TB{1,7} ];
%--------------------- 8 -----------------------------------
C_Tsai=tsai(M1, M2)
T_Tsai = (transl(C_Tsai))';
C_Tsai_rad = tr2rpy(C_Tsai);
C_Tsai_rpy_rx_ry_rz =rad2deg(C_Tsai_rad);
Q_Tsai_Qxyzw=Quaternion(C_Tsai);
fprintf('Tsai(rad) = \n%f, %f, %f, %f, %f, %f\n',T_Tsai(1,1), T_Tsai(1,2), T_Tsai(1,3), C_Tsai_rad(1,1), C_Tsai_rad(1,2), C_Tsai_rad(1,3));
fprintf('Tsai(deg) = \n%f, %f, %f, %f, %f, %f\n\n',T_Tsai(1,1), T_Tsai(1,2), T_Tsai(1,3), C_Tsai_rpy_rx_ry_rz(1,1), C_Tsai_rpy_rx_ry_rz(1,2), C_Tsai_rpy_rx_ry_rz(1,3));
fprintf('Tsai(Qxyzw) = \n %f, %f, %f, %f\n\n', Q_Tsai_Qxyzw.v(1), Q_Tsai_Qxyzw.v(2), Q_Tsai_Qxyzw.v(3), Q_Tsai_Qxyzw.s);
稍微解释一下,程序做的就是读入机器人和相机的两两姿态信息,转换为4x4 的齐次变换矩阵,送入tsai.m程序求解。
手眼标定eye in hand 和eye to hand 的区别主要是机器人那边,一个是end相对于base,另一个是base相对于end。千万注意。
====================平面九点标定法====================
当利用RGB相机或者是机器人只进行平面抓取(也即固定姿态抓取,机器人六自由度位置和姿态简化为只考虑平移,姿态人为给定并且固定,这时机器人可以移动到目标点上方),问题可以简化为平面RGB图像的目标像素点集A(x1,y1)与机器人在平面(X1,Y1)的点对关系。具体做法是相机识别像素点给到A,然后利用示教器查看机器人在基座标系下的坐标,当做B。

相机坐标和机器人坐标写成齐次的形式,投影矩阵X是一个3x3的矩阵我们需要6组对应点来求解最小配置解。利用奇异值分解SVD来求取。
D:\opencv_work\cubeSolver\cv_solver\ConsoleApplication1\CV_SVD.cpp
D:\Matlab_work\handeye\NinePoints_Calibration.m
//Solve equation:AX=b
#include <cv.h>
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main(int argc, char** argv)
{
printf("\nSolve equation:AX=b\n\n");
//Mat A = (Mat_<float>(6, 3) <<
//480.8, 639.4, 1,
//227.1, 317.5, 1,
//292.4, 781.6, 1,
//597.4, 1044.1, 1,
//557.7, 491.6, 1,
//717.8, 263.7, 1
// );// 4x3
//Mat B = (Mat_<float>(6, 3) <<
//197170, 185349, 1,
//195830, 186789, 1,
//196174, 184591, 1,
//197787, 183176, 1,
//197575, 186133, 1,
//198466, 187335, 1
// );
Mat A = (Mat_<float>(4, 3) <<
2926.36, 2607.79, 1,
587.093, 2616.89, 1,
537.031, 250.311, 1,
1160.53, 1265.21, 1);// 4x3
Mat B = (Mat_<float>(4, 3) <<
320.389, 208.197, 1,
247.77, 209.726, 1,
242.809, 283.182, 1,
263.152, 253.715, 1);
Mat X;
cout << "A=" << endl << A << endl;
cout << "B=" << endl << B << endl;
solve(A, B, X, CV_SVD);
cout << "X=" << endl << X << endl;
Mat a1 = (Mat_<float>(1, 3) << 1864, 1273, 1);
Mat b1 = a1*X;
cout << "b1=" << endl << b1 << endl;
cout << "真实值为:" << "283.265, 253.049, 1" << endl;
getchar();
return 0;
}
结果对比:左halcon C#(第三列为0,0,1,没做显示),右opencv c++,底下为Matlab结果,三者一致,算法检测通过。

=============
四轴平面机器人的手眼标定_Stones1025的博客-CSDN博客
这种方法利用点对,求仿摄变换矩阵
#include "pch.h"
#include <iostream>
#include <cv.h>
#include<opencv2/opencv.hpp>
using namespace cv;
int main(int argc, char** argv)
{
printf("\nSolve equation:AX=b\n\n");
Point2f srcTri[3];
srcTri[0] = Point2f(480.8f, 639.4f);
srcTri[1] = Point2f(227.1f, 317.5f);
srcTri[2] = Point2f(292.4f, 781.6f);
Point2f dstTri[3];
dstTri[0] = Point2f(197170.0f, 185349.0f);
dstTri[1] = Point2f(195830.0f, 186789.0f);
dstTri[2] = Point2f(196174.0f, 184591.0f);
Mat warp_mat = getAffineTransform(srcTri, dstTri);
// 计算图像坐标
std::cout << "img_corners:\n" << srcTri << std::endl;
std::cout << "robot_corners:\n" << dstTri << std::endl;
std::cout << warp_mat << std::endl;
//
//[5.284835627018051, -0.00236967559639317, 194630.5662011061;
//0.4056177440315953, -4.793119669651512, 188218.6997054448]
return 0;
}================= Eye in hand 数据及Ground truth =========================
Marker in Camera 八组数据,单位:米及弧度,姿态用的是RotVector表示
0.11725,0.05736,0.32176,0.02860,-0.1078,3.06934
0.07959,0.06930,0.29829,0.66126,-0.2127,2.99042
0.14434,0.03227,0.40377,-0.9465,-0.1744,2.80668
0.11008,0.05605,0.35730,0.12422,-1.0665,2.87604
0.1131,0.0438171,0.299624,-0.058278,-0.514154,-3.06309
0.057039,0.109464,0.415275,0.414777,0.750109,-2.49495
0.13702,0.00520,0.38190,0.26431,-0.7554,2.26885
-0.03670,-0.04433,0.237292,0.807501,-0.27347,0.614594
Robot end-effector in Base 八组数据,单位:米及弧度,姿态用的是RotVector表示
0.400422,-0.0262847,0.365594,3.12734,-0.0857978,-0.0168582
0.423347,-0.16857,0.340184,-2.73844,0.089013,0.123284
0.42540,0.19543,0.29062,2.44351,-0.1777,-0.0722
0.58088,-0.0541,0.32633,-2.9303,0.06957,0.98985
0.2760,-0.033,0.3301,3.0813,0.0724,0.6077
0.54011,0.09071,0.34623,2.62279,0.75876,-0.6927
0.57732,-0.1346,0.37990,-2.6764,1.04868,0.82177
0.27844,-0.1371,0.28799,-0.8233,2.26319,0.36110
Ground truth:Camera in end-effector
Calibration Result:
-0.005816946773 -0.997849042178 -0.065295115862 0.053457653403
0.999355366046 -0.003487653357 -0.035730779845 -0.009463725064
0.035426197714 -0.065460868457 0.997226082298 -0.045113271057
0 0 0 1
RotVector(rad): -0.023440 -0.079412 1.57466
AngVector(rad): 1.576836 <-0.014865, -0.050362, 0.998620>
AngVector(deg): 90.346026 <-0.014865, -0.050362, 0.998620>
rx_ry_rz_rw: -0.010543 -0.079412 1.574660 0.704968
rx_ry_rz_rw_norm: -0.010543 -0.035718 0.708260 0.704968
后续自己用Qt做了一个简易的手眼标定求解程序,界面供大家参考。离线读入机器人和相机数据(8组),求解手眼标定结果

眼在手,机器人末端相对于基坐标,单位:米。姿态用的是四元数Quaternion表示(8组)
0.400422, -0.0262847, 0.365594, 0.999588151, -0.02742345388, -0.00538836742, 0.006515220837
0.423347, -0.16857, 0.340184, -0.9786646936, 0.03181149865, 0.04405928123, 0.1981469805
0.4254, 0.19543, 0.29062, 0.9380939859, -0.06822124784, -0.02771848111, 0.3384630271
0.58088, -0.0541, 0.32633, -0.9468961176, 0.02248082548, 0.319859783, 0.02391807321
0.276, -0.033, 0.3301, 0.9808407319, 0.02304639892, 0.1934433235, 5.201755801e-05
0.54011, 0.09071, 0.34623, 0.9188632814, 0.2658225414, -0.2426792061, 0.1616646203
0.57732, -0.1346, 0.3799, -0.8926332014, 0.3497558607, 0.2740768143, 0.07588613509
0.27844, -0.1371, 0.28799, -0.3172132084, 0.8719953371, 0.1391299521, 0.3458941585
Marker in Camera 八组数据,单位:米。姿态用的是四元数Quaternion表示(8组)
0.11725, 0.05736, 0.32176, 0.009306078775, -0.03507675846, 0.9987244694, 0.03510629645
0.07959, 0.0693, 0.29829, 0.2152538, -0.06923824706, 0.9734435298, 0.03577095343
0.14434, 0.03227, 0.40377, -0.3177842722, -0.05855422828, 0.9423336091, 0.08713166949
0.11008, 0.05605, 0.3573, 0.04043751376, -0.347179266, 0.9362414029, 0.03582457685
0.1131, 0.0438171, 0.299624, -0.01875719888, -0.1654842107, -0.9858778323, 0.01755115881
0.057039, 0.109464, 0.415275, 0.1522703983, 0.2753754335, -0.9159308017, 0.2491041208
0.13702, 0.0052, 0.3819, 0.1025108419, -0.2929767695, 0.879958093, 0.3596246576
-0.0367, -0.04433, 0.237292, 0.3854232814, -0.1305282653, 0.2933480407, 0.8650769868
//======================== 2022
Moveit 上有个插件,利用的是 ChArUco,精度更好,也避免了棋盘格需要视野中整张看到的问题
ros-planning/moveit_calibration: Hand-eye calibration tools for robot arms. (github.com)
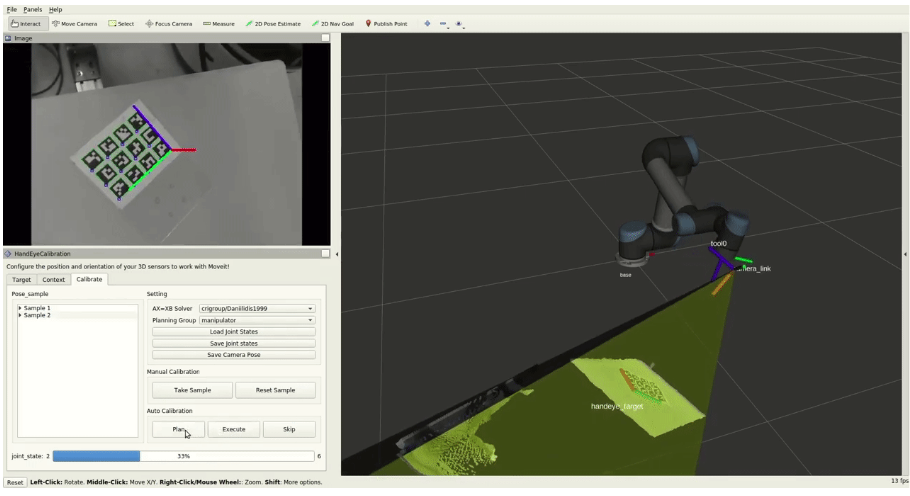
handeye-calib: 基于ROS的手眼标定程序,支持眼在手上,眼在手外。提供完整文档。欢迎关注公众号鱼香ROS。 (gitee.com)










 本文详细介绍了机器人手眼标定的过程,包括eye in hand和eye to hand两种模式,阐述了数学描述和AX=XB问题的求解方法。通过实例展示了在Matlab中进行标定解算,并提供了相关资源和参考资料,如平面九点法标定和基于ROS的解决方案。
本文详细介绍了机器人手眼标定的过程,包括eye in hand和eye to hand两种模式,阐述了数学描述和AX=XB问题的求解方法。通过实例展示了在Matlab中进行标定解算,并提供了相关资源和参考资料,如平面九点法标定和基于ROS的解决方案。

















 2423
2423

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










