1D and 2D Gaussian Derivatives

最新推荐文章于 2024-08-21 23:25:24 发布

O天涯海阁O

最新推荐文章于 2024-08-21 23:25:24 发布

阅读量932

点赞数

分类专栏：数学知识文章标签： elasticsearch 大数据 big data

原文链接：http://campar.in.tum.de/Chair/HaukeHeibelGaussianDerivatives

版权

数学知识专栏收录该内容

12 篇文章

订阅专栏

http://campar.in.tum.de/Chair/HaukeHeibelGaussianDerivatives

在这里插入图片描述

The Two-Dimensional Case
Base Function (0th order)
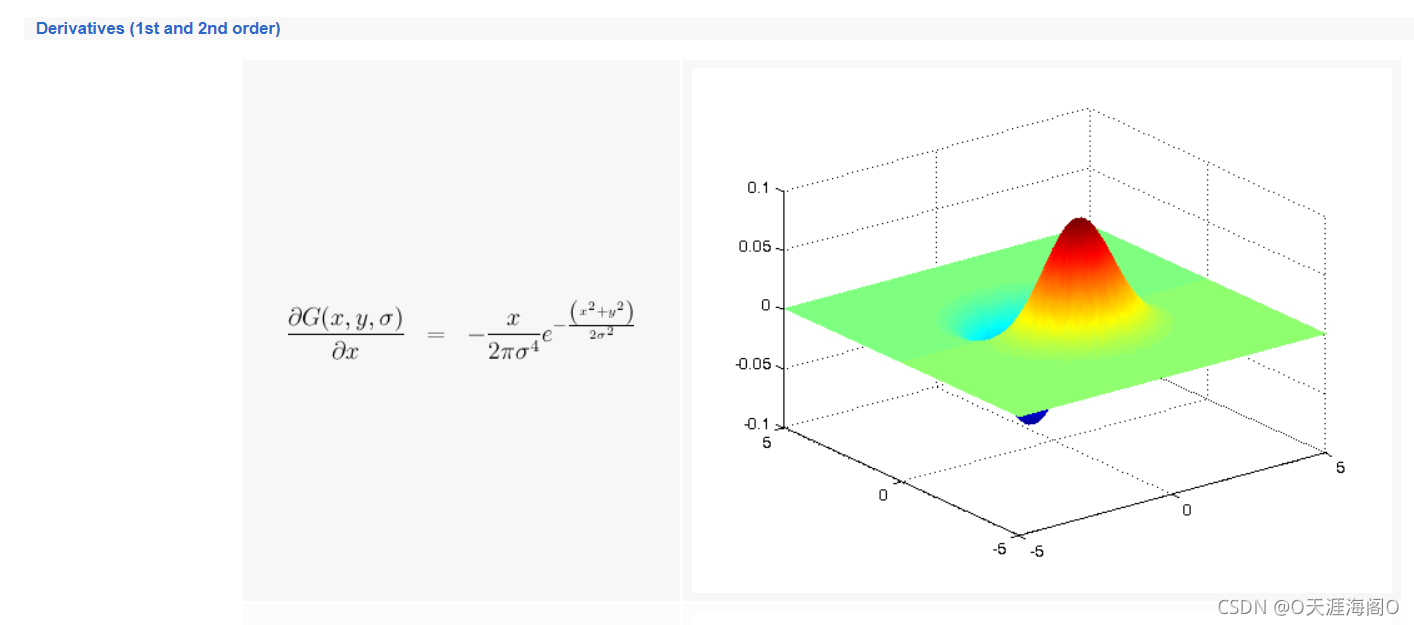
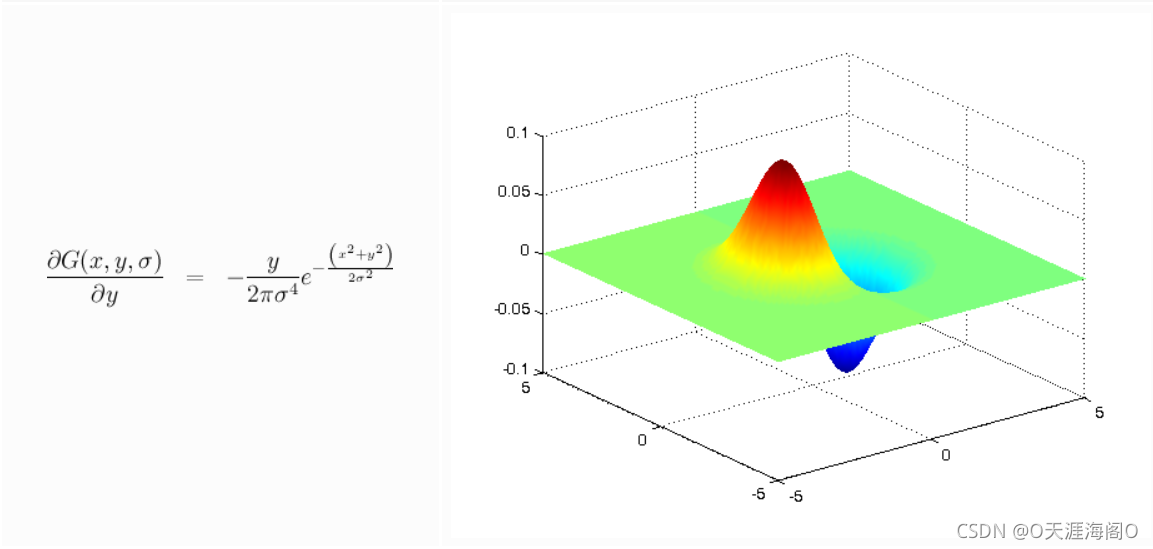
在这里插入图片描述

在这里插入图片描述

Computes discrete 1D gaussian functions

function [ gaussian ] = gaussian( x, sigma, order, normalize )
        if isempty(normalize)
            normalize = false;
        end
        
        gaussian_base = exp(-(x.*x)/(2*sigma^2));
        
        % we will do the same as ITK. this is just done to be able to
        % compare gaussian results with those coming from ITK.
        if (normalize)
            gaussian_base = sigma*gaussian_base;
        end
            
        if order == 0            
            gaussian = 1/(sigma*sqrt(2*pi)) .* gaussian_base;
        elseif order == 1
            gaussian = -x./(sigma^2*sqrt(2*pi)) .* gaussian_base;
        elseif order == 2
            gaussian = - gaussian_base ./ (sigma^3*sqrt(2*pi)) + x.*x.*gaussian_base / (sigma^5*sqrt(2*pi));
        end
end

Computes discrete 2D gaussian functions

function [ gaussian2d ] = gaussian2d( x, y, sigma, order_x, order_y, normalize )
	if (nargin<6)
        normalize = false;
    end        
        
    gaussian2d_base = exp( -(x.*x + y.*y) / (2*sigma^2) );
    
    % we will do the same as ITK. this is just done to be able to
    % compare gaussian results with those coming from ITK.
	if (normalize)
    	gaussian2d_base = sigma^2*gaussian2d_base;
	end    
    
    if (order_x == 0 && order_y ==0)
        scale = 1 / (2*pi*sigma^2);
        gaussian2d = scale .* gaussian2d_base;
    elseif (order_x == 1 && order_y == 0)
        scale = - x / (sigma^4*2*pi);
        gaussian2d = scale .* gaussian2d_base;
    elseif (order_x == 0 && order_y == 1)
        scale = - y / (sigma^4*2*pi);
        gaussian2d = scale .* gaussian2d_base;    
    elseif (order_x == 2 && order_y == 0)
        t1 = - gaussian2d_base / (sigma^4*2*pi);
        t2 = x .* x .* gaussian2d_base / (sigma^6*2*pi);
        gaussian2d = t1 + t2;
    elseif (order_x == 0 && order_y == 2)
        t1 = - gaussian2d_base / (sigma^4*2*pi);
        t2 = y .* y .* gaussian2d_base / (sigma^6*2*pi);
        gaussian2d = t1 + t2;
    elseif (order_x == 1 && order_y == 1)
       gaussian2d = x .* y .* gaussian2d_base / (2*pi*sigma^6);
    end
end