简明扼要的介绍下不同滤波方案的联系和区别,重点突出ESKF。
一、几种滤波的共同点:
1.本质上都是概率的运算,最核心的思想是贝叶斯概率,也就是先验问题与后验问题的定义与其概率计算;
2.各算法的推导过程和最终形态以及求解公式,本质上都离不开KF的经典5大公式;具体可参考贺博的”卡尔曼滤波 -- 从推导到应用“系列。
3.无论是否迭代,kF系列算法都基于马尔科夫假设,也就是只与上一帧数据进行参比计算,因此其结果精确性与稳定性相比最新的一些算法或后端图优化来说,还是有一些逊色。
二、区别:
1.KF主要是针对线性估计
2. EKF通过对目标函数的二阶泰勒式子进行截断来使非线性的内容线性化,从而完成非线性估计,但其截断误差会影响结果,持续下去也会发散;
3. UKF通过对目标函数的分布进行特征点采样,采用高斯的 σ 原则,选取特征点来模拟分布;
4. PF则是与目标函数本身关系不大,使用大量的粒子描述原目标函数的分布,经过权重筛选和重采样,不断将模拟的结果作为分布的结果输入,获得滤波的结果;
5. ESKF是一种间接的滤波法,它不是对目标函数求解,而是对系统误差状态求解,最后和名义状态进行合并,得到实际状态。
6. 计算复杂度:EKF由于雅克比矩阵的计算,其复杂度相对较高,时间消耗大,而UKF消耗受限于关键点的选取,PF除了受限于粒子数目外,还受限于采样方法;ESKF与KF是计算比较快的算法。
三、ESKF介绍:
1. ESKF的核心思想是把系统状态分为三类:
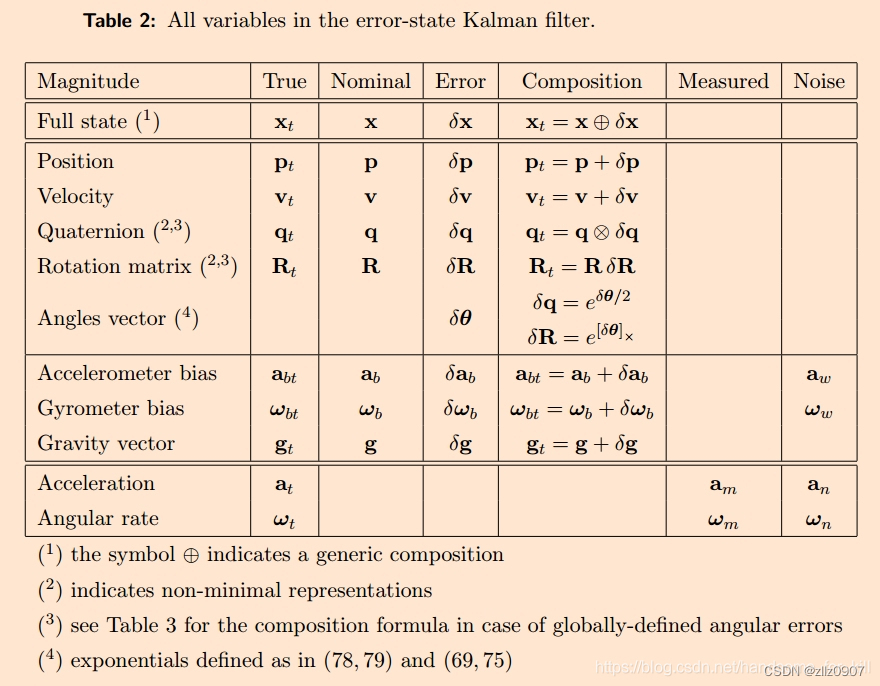
a. True State(Ground Truth):真值,指系统实际的运行状态,一般我们会在系统中假定某种输入为真值。(这一条在非线性KF系列滤波通用);
b. Nominal State:名义状态,指系统的变化情况或变化趋势。例如IMU的各轴向加速度对时间的积分可以认为是各轴向距离上的变化,一般在系统中我们认为它是非线性(这一条也是我们在非线性KF中的强关注点);
c. Error State:误差状态,真值与名义状态的差值,这个值也是非线性变化的。例如在IMU、激光、毫米波的系统中,我们可以假定激光的数据为真值,用其他两种来做融合,结果与激光做RMSE,这就可以认为是一种误差状态。
那么我们可以将任意一个状态变化过程,分割为名义变化过程和误差项,即真值为名义变化过后的结果与误差值的叠加。
2. ESKF的步骤如下:
a. 对IMU数据进行积分,获得名义状态X,注意这个X并没有考虑噪声,所以必然引入了累计误差;
b. 利用KF算法估计Error State,包括状态更新和测量更新,这个过程是考虑了噪声的,而且由于这个误差状态的方程式近似线性的,直接使用KF就可以;
c. 利用Error State修正Nominal State,获取“真值”;
d. 重置Error State,等待下一次更新;
3. 使用ESKF的优势:
a. Error State中的参数数量与运动自由度是相等的,避免了过参数化引起的协方差矩阵奇异的风险;
b. Error State总是接近于0,Kalman Filter工作在原点附近。因此,远离奇异值、万向节锁,并且保证了线性化的合理性和有效性;
c. Error State总是很小,因此二阶项都可以忽略,因此雅可比矩阵的计算会很简单,很迅速;
d. Error State的变化平缓,因此KF修正的频率不需要太高。
参考:
1. Joan Sol`a. Quaternion kinematics for the error-state KF. Sep 12, 2016.
























 255
255

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








