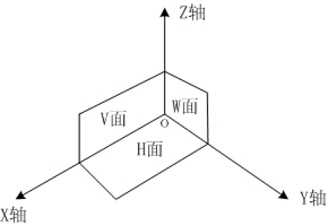
在工程上将三维坐标系OXYZ中的三个坐标平面分别设为H面(XOY平面)、V面(XOZ平面)、W面(YOZ平面)。
所谓正投影就是三维图形上各点分别向某一坐标平面作垂线,其垂足便称为各个三维点的投影点,将所有投影点按原三维图形中点与点之间的对应关系一一连起来便得到了一平面图形,该平面图形就称为三维图形在该坐标平面上的正投影。
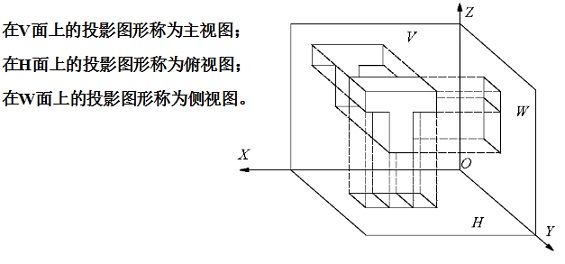
V面投影(主视图)
物体在XOZ平面上的正投影,坐标y=0,坐标x和z保持不变,其变换矩阵为:
即:[x y z 1]*TV = [x 0 z 1] = [x’ y’ z’ 1]
H面投影(俯视图)
先将物体向XOY平面作正投影(即坐标z=0),然后将得到的投影绕X轴顺时针旋转90度,使其与V面共面,再沿-Z方向平移一段距离n,以使H面投影和V面投影之间保持一段距离。变换矩阵为:
即:[x y z 1]*TH = [x 0 –y–n 1] = [x’ y’ z’ 1]
W面投影(侧视图)
先将物体向YOZ平面作正投影(即坐标x=0),然后绕Z轴逆时针旋转90度,使其与V面共面,为保证与V面投影有一段距离,再沿-X方向平移一段距离k,变换矩阵为:
即:[x y z 1]*TW = [-y-k 0 z 1] = [x’ y’ z’ 1]








 本文介绍了三维坐标系中正投影的基本概念及其在不同坐标平面上的变换矩阵,包括V面投影(主视图)、H面投影(俯视图)和W面投影(侧视图)。这些变换对于理解和应用三维图形的二维表示至关重要。
本文介绍了三维坐标系中正投影的基本概念及其在不同坐标平面上的变换矩阵,包括V面投影(主视图)、H面投影(俯视图)和W面投影(侧视图)。这些变换对于理解和应用三维图形的二维表示至关重要。

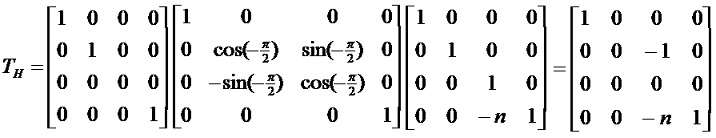

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








