分数质量-弹簧-阻尼系统研究（Matlab代码实现）

最新推荐文章于 2025-11-07 19:03:15 发布

原创最新推荐文章于 2025-11-07 19:03:15 发布 · 268 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #数据库 #sql #支持向量机

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

分数质量-弹簧-阻尼系统研究

摘要：本文聚焦于分数质量-弹簧-阻尼系统（Fractional-Order Mass-Spring-Damper System, FMSDS）的研究。传统整数阶质量-弹簧-阻尼系统在描述复杂系统阻尼特性时存在局限，而分数阶微积分凭借其记忆效应和非局部性优势，能更精准地模拟实际系统行为。本文阐述了分数阶微积分基本概念，构建FMSDS数学模型，分析其动力学特性，探讨分数阶导数对系统振动行为的影响，并展望该系统在工程领域的潜在应用。

关键词：分数阶微积分；质量-弹簧-阻尼系统；动力学分析；分数阶导数；工程应用

一、引言

近年来，国内外专家开始将环形弹簧引入到结构减震领域，对其开展了初步的研究。Filiatrault 等设计了一种含有常规环形弹簧的减震装置，并基于振动台试验考察了其减震性能。Khoo 等研制了一种钢框架基于环形弹簧的钢框架结构耗能节点。Fang 等提出了一种含有超弹性环形弹簧的钢框架结构自复位耗能型梁柱节点。Issa 等研发了一种活塞型环形弹簧自复位耗能支撑。以上研究表明，环形弹簧是一种兼具耗能和自复位特性的减震部件，可用于新型自复位控制系统的研制。

尽管国内外学者对基于环形弹簧的建筑结构减震控制开展了初步的研究，但是，环形弹簧减震器的研究基础仍然十分薄弱，相关的理论和试验研究偏少。本文研究分数质量-弹簧-阻尼器系统（FMSDS）数学模型的数值解。

质量-弹簧-阻尼系统（Mass-Spring-Damper System, MSDS）作为经典的力学模型，在振动控制、机械工程、土木工程等众多领域有着广泛应用。传统MSDS采用整数阶微分方程描述，但在实际应用中，许多复杂系统呈现出非理想的阻尼特性，如材料的黏弹性行为、结构的复杂连接以及流体的非牛顿性质等，这些特性难以用传统整数阶模型精确刻画。

分数阶微积分作为整数阶微积分的推广，近年来受到学术界广泛关注。它具有记忆效应和非局部性，能更精准地描述复杂系统的阻尼特性。分数阶导数可理解为过去状态的加权平均，使分数阶模型能够捕捉系统历史的影响，从而更好地模拟实际系统行为。因此，研究分数质量-弹簧-阻尼系统（FMSDS）的动力学特性，探索分数阶导数对系统振动行为的影响，具有重要的理论意义和实际应用价值。

二、分数阶微积分基本概念

分数阶微积分将微分和积分的阶数推广到非整数域，目前存在多种定义分数阶导数和积分的方法，常用的有Riemann-Liouville定义、Grünwald-Letnikov定义和Caputo定义。

（一）Riemann-Liouville定义

对于函数 f(t)，Riemann-Liouville定义的分数阶积分和导数分别为：

（二）Grünwald-Letnikov定义

Grünwald-Letnikov定义的分数阶导数表示为：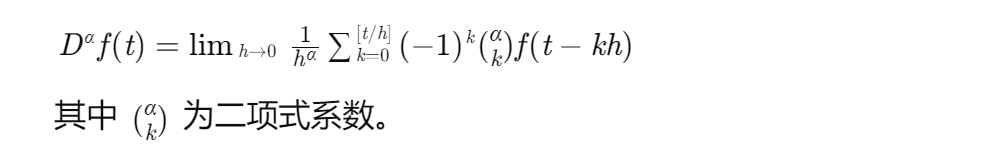

（三）Caputo定义

Caputo定义的分数阶导数为：

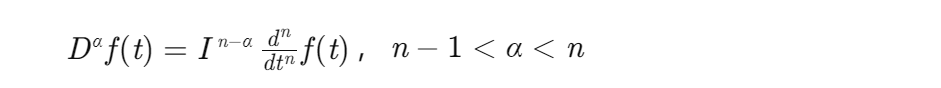
Caputo定义与Riemann-Liouville定义的主要区别在于求导和积分的顺序。Caputo定义允许在 t=0 处具有整数阶导数的初始条件，在工程应用中更为方便，本文采用Caputo定义来描述分数阶导数。

三、FMSDS数学模型构建

四、FMSDS动力学分析

FMSDS的动力学分析主要包括求解运动方程以及分析系统的振动特性和稳定性。由于分数阶微分方程通常难以获得解析解，一般采用数值方法进行求解，如广义Adams-Bashforth-Moulton预测-校正算法等。

（一）分数阶导数对系统振动频率的影响

研究结果表明，分数阶导数的阶数 α 对系统的振动频率有显著影响。随着 α 的减小，系统的振动频率会略微降低。这是因为分数阶导数引入了记忆效应，使系统对过去状态的响应更加敏感，从而降低了系统的振动频率。例如，在某些具有黏弹性材料的结构中，采用分数阶模型能更准确地模拟其振动频率特性，相较于传统整数阶模型，能更好地反映实际结构的振动情况。

（二）分数阶导数对系统阻尼特性的影响

分数阶导数能够更灵活地调整系统的阻尼特性。传统整数阶模型中，阻尼系数 c 是一个固定的参数，难以精确描述复杂系统的阻尼行为。而在FMSDS中，分数阶导数的阶数 α 和阻尼系数 c 共同作用，可以模拟出多种不同的阻尼特性。例如，当 α 取不同值时，系统可以表现出类似欠阻尼、临界阻尼和过阻尼的不同振动响应，但与整数阶模型相比，其阻尼特性更加丰富和复杂，能更好地适应不同实际系统的需求。

（三）分数阶导数对系统稳定性的影响

系统的稳定性是系统正常运行的重要前提。分数阶导数的引入对系统的稳定性产生了新的影响。通过分析系统的特征方程或利用数值模拟方法，可以研究不同参数条件下系统的稳定性。研究发现，分数阶导数的阶数 α 和系统参数（如质量 m、阻尼系数 c、弹簧劲度系数 k 等）之间存在复杂的相互作用关系，共同影响着系统的稳定性。在某些情况下，适当的分数阶导数阶数可以使系统更加稳定，而在另一些情况下，不当的参数组合可能导致系统出现不稳定现象。因此，在设计FMSDS时，需要综合考虑分数阶导数阶数和系统参数的选择，以确保系统具有良好的稳定性。

五、FMSDS在工程领域的潜在应用

（一）振动控制领域

在机械工程中，许多设备在运行过程中会产生振动，过大的振动不仅会影响设备的性能和寿命，还可能产生噪声污染。FMSDS可以作为一种有效的振动控制模型，通过调整分数阶导数的阶数和系统参数，设计出合适的振动控制器，实现对机械振动的有效抑制。例如，在汽车悬挂系统中，采用FMSDS模型可以更好地模拟车辆在不同路况下的振动特性，从而设计出更优的悬挂系统参数，提高车辆的行驶平顺性和舒适性。

（二）结构抗震设计

在土木工程领域，建筑物的抗震设计至关重要。FMSDS可以用于模拟建筑物在地震作用下的振动响应，通过考虑材料的黏弹性等复杂特性，更准确地预测建筑物在地震中的受力情况和变形情况。基于FMSDS模型的分析结果，可以优化建筑物的结构设计，合理设置阻尼器等减震装置，提高建筑物的抗震能力，保障人们的生命财产安全。

（三）生物医学工程

在生物医学工程中，FMSDS也有潜在的应用价值。例如，在研究人体组织的力学特性时，人体组织往往表现出复杂的黏弹性行为，传统整数阶模型难以准确描述。FMSDS可以更好地模拟人体组织的力学响应，为生物医学研究和临床治疗提供更准确的模型支持。例如，在人工关节的设计中，利用FMSDS模型可以更好地模拟关节软骨的力学特性，设计出更符合人体生理需求的人工关节，提高患者的生活质量。

六、结论与展望

本文对分数质量-弹簧-阻尼系统进行了深入研究，构建了FMSDS的数学模型，分析了其动力学特性，探讨了分数阶导数对系统振动行为的影响，并展望了该系统在工程领域的潜在应用。研究结果表明，分数阶微积分能够为质量-弹簧-阻尼系统的建模和分析提供更强大的工具，分数阶导数的引入使系统能够更精确地描述复杂系统的阻尼特性，具有更丰富的动力学行为。

然而，目前FMSDS的研究仍处于发展阶段，还存在一些有待进一步研究的问题。例如，如何更高效地求解分数阶微分方程，提高数值计算的精度和速度；如何更准确地确定分数阶导数的阶数和系统参数，以更好地模拟实际系统；如何将FMSDS与其他先进的控制理论和方法相结合，实现对复杂系统的更有效控制等。未来的研究可以围绕这些问题展开，进一步推动FMSDS理论的发展和应用，为工程实践提供更可靠的理论支持和技术保障。

📚2 运行结果

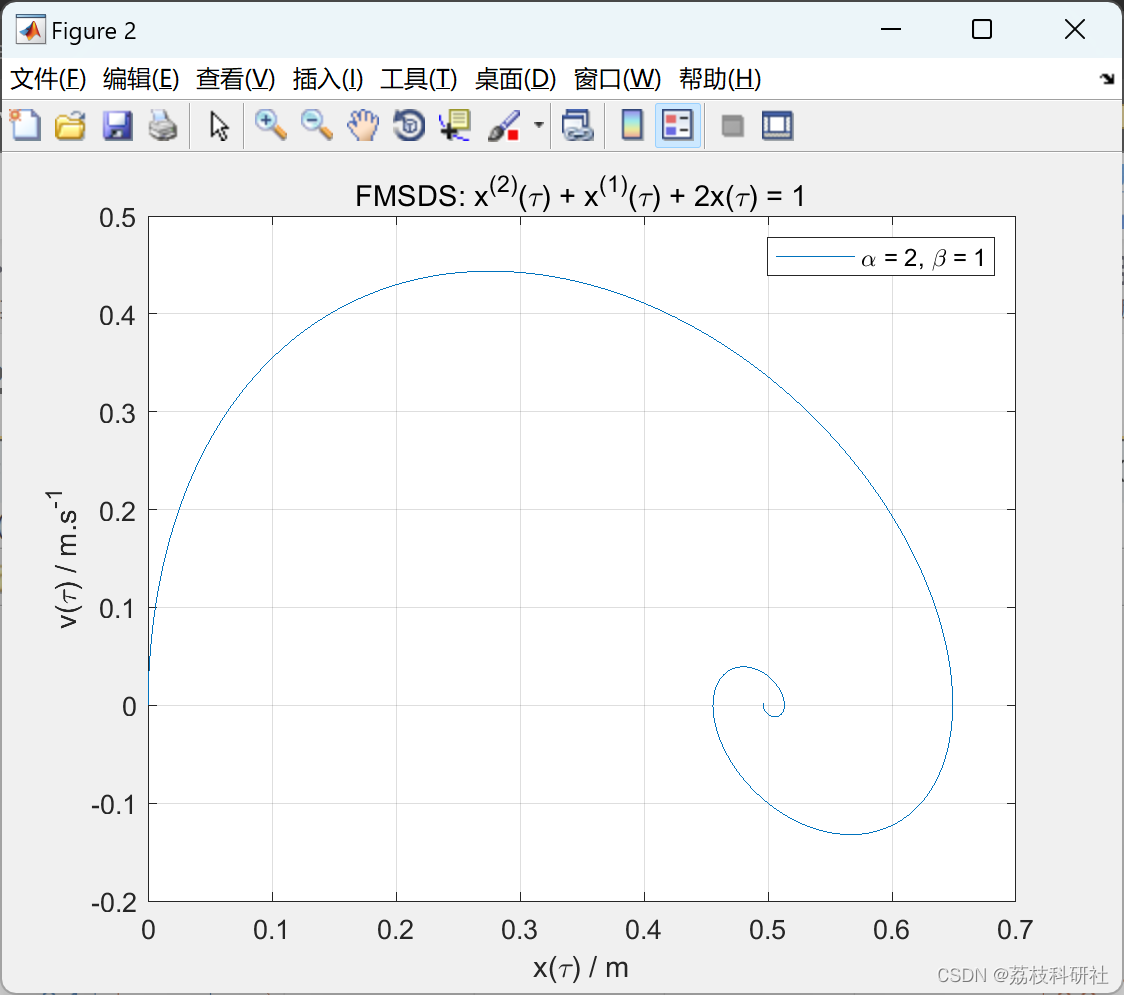
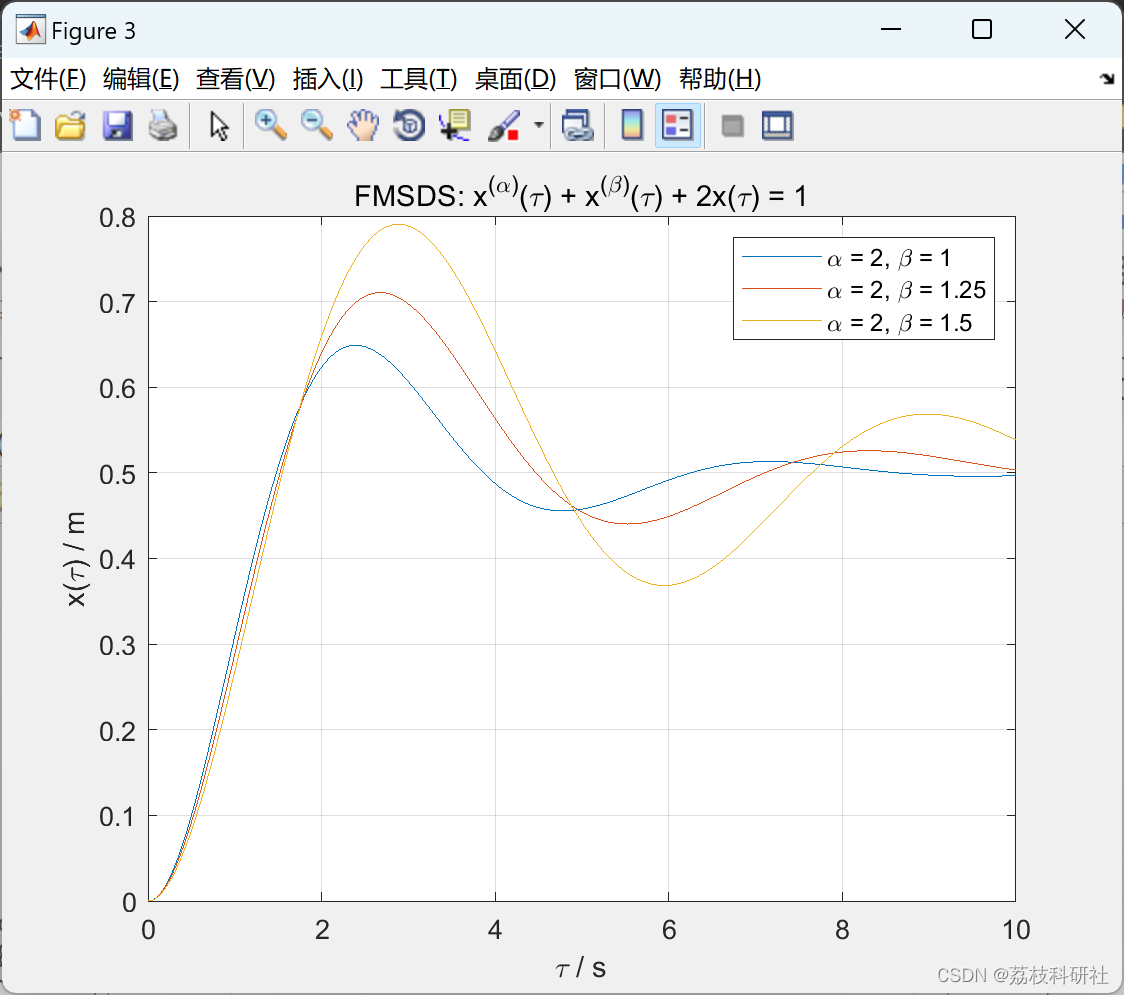
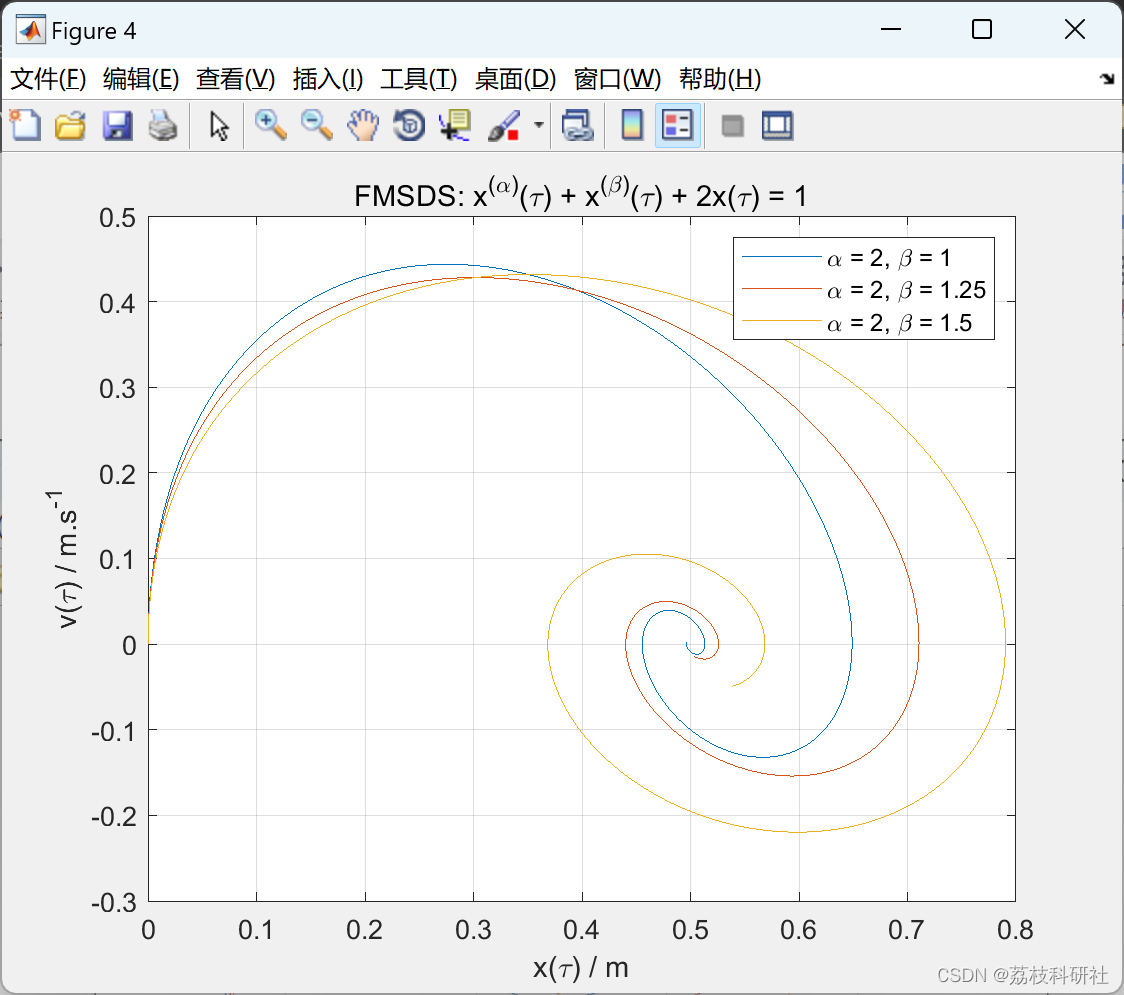
部分代码：

function[t,x,v]= FMSDS(m,b,k,alpha,beta,tau,dtau,x0,v0,f)
%
% DESCRIPTION:
%
% Function returns numerical solution of the
% Fraction Mass-Spring-Damper System (FMSDS)
% using Grunwald-Letnikov derivative definition.
%
% |
% /| Damper --------
% /| -- | |
% /|--- |-------| Mass | Force
% /| -- b | m |<--------> f
% /| Spring | |
% /|-/\/\/\/\---| |
% /| k --------
% /| | Displacement, x
% /|<------------------------------>
% /| | Velocity, v
% 0
%
% Fractional differential equation:
%
% d^alpha d^beta
% m ---------- x(t) + b -------- x(t) + k x(t) = f for 0 <= t <= tau
% d t^alpha d^beta alpha > beta
%
% Initial conditions:
% x(0) = x0
% x'(0) = v(0) = v0
%
% Grunwald-Letnikov definition:
%
% Nf
% sum b_j.y(t-j.dtau)
% d^alpha j=0
% --------- y(t) = -------------------
% d t^alpha dtau^alpha
%
% Difference equation :
%
% p p
% sum bc_j.x(p-j) sum cc_j.x(p-j)
% j=0 j=0
% m --------------- + b --------------- + k.x(p) = f
% dtau^alpha dtau^beta
%
% or
% p
% m.dtau^(-alpha) ( bc_0.x(p) + sum bc_j.x(p-j) ) +
% j=1
%
% p
% + b.dtau^(-beta) ( cc_0.x(p) + sum cc_j.x(p-j) ) + k.x(p) = f
% j=1
%
% or
% p p
% x(p)=(f-m.dtau^(-alpha) sum bc_j.x(p-j)-b.dtau^(-beta) sum cc_j.x(p-j))/
% j=1 j=1
%
% (m.dtau^(-alpha).bc_0 + b.dtau^(-beta).cc_0 + k)
%
% INPUTS:
% m - mass [ kg ]
% b - damper coefficient [ kg/s ]
% k - stiffness (or spring constant) [ kg/s^2 ]
% alpha - fractional-order derivative [ - ]
% beta - fractional-order derivative [ - ]
% tau - simulation time [ s ]
% dtau - time step [ s ]
% x0 - initial displacement [ m ]
% v0 - initial velocity [ m/s ]
% f - force [ N ]
%
% OUTPUTS:
% t - vector of time [ s ]
% x - vector of distance [ m ]
% v - vector of velocity [ m/s ]
%
% AUXILIARY VARIABLES:
% n - length of time vector
% p, i, j - index
% bc, cc - binomial coefficients
% s1, s2 - sum

%
n = tau/dtau+1;

t(1) = 0.0;
x(1) = x0;
v(1) = v0;

t(2) = dtau;
x(2) = x(1) + dtau*v(1);
v(2) = ( x(2) - x(1) )/dtau;

p = 1;
for i = 3:n
p = p + 1;
t(i) = (i-1)*dtau;

bc = zeros(1,p+1);
cc = zeros(1,p+1);
bc(1) = 1;
cc(1) = 1;
for j = 2:p+1
bc(j) = (1 - (1+alpha)/(j-1))*bc(j-1);
cc(j) = (1 - (1+beta)/(j-1))*cc(j-1);
end

s1 = 0;
s2 = 0;
for j = 2:p+1
s1 = s1 + bc(j)*x(p+2-j);
s2 = s2 + cc(j)*x(p+2-j);
end

x(i) = ( f - m*dtau^(-alpha)*s1 - b*dtau^(-beta)*s2 )/...
( m*dtau^(-alpha)*bc(1) + b*dtau^(-beta)*cc(1) + k);
v(i) = ( x(i) - x(i-1) )/dtau;
end
end