动手学运动规划:1.1 车辆运动学:自行车模型

七岁的那一年，抓住那只蝉，以为能抓住夏天。—如烟 五月天

🏰代码及环境配置：请参考0.2 环境配置和代码运行 | 自动驾驶小白说!

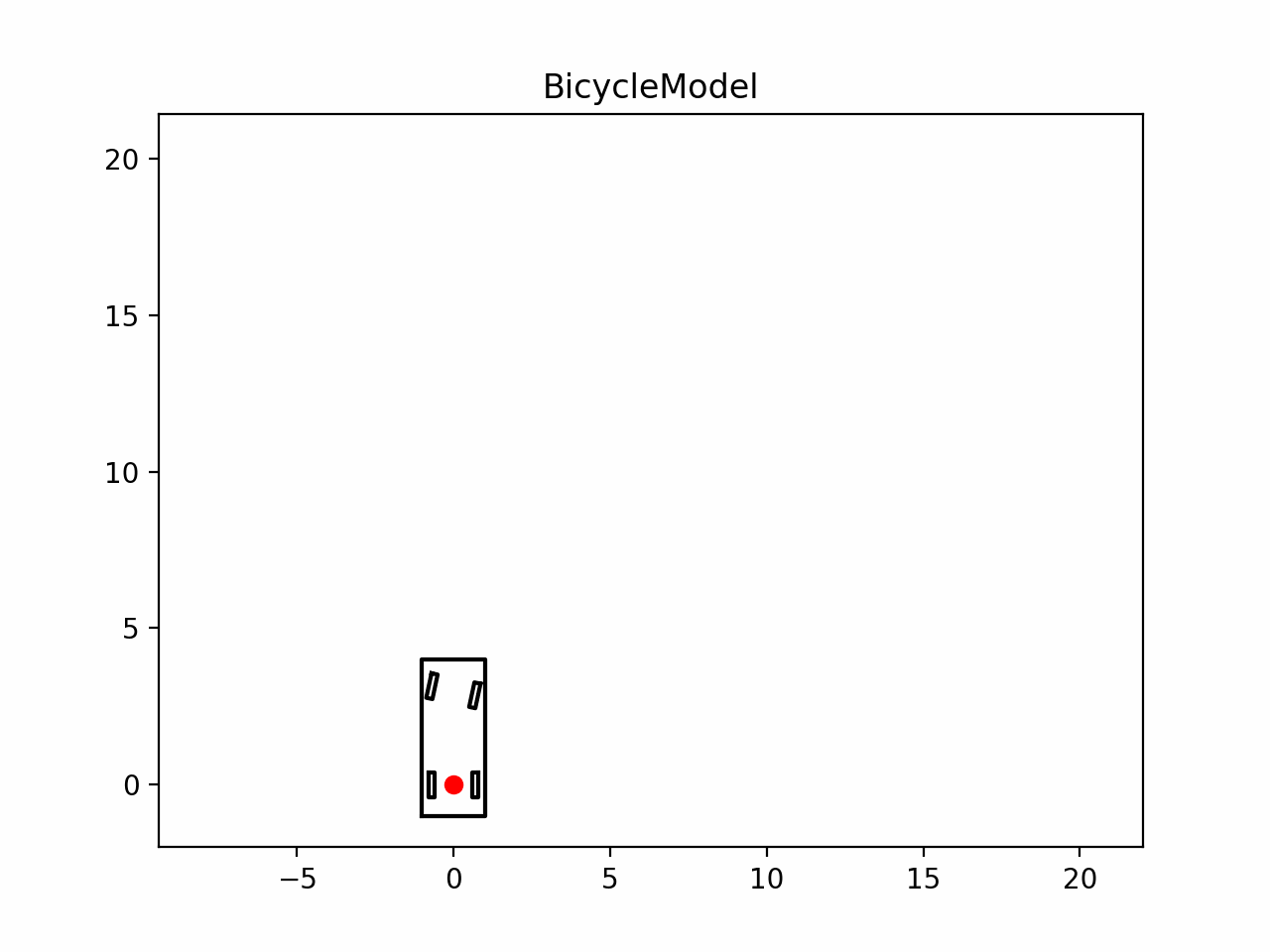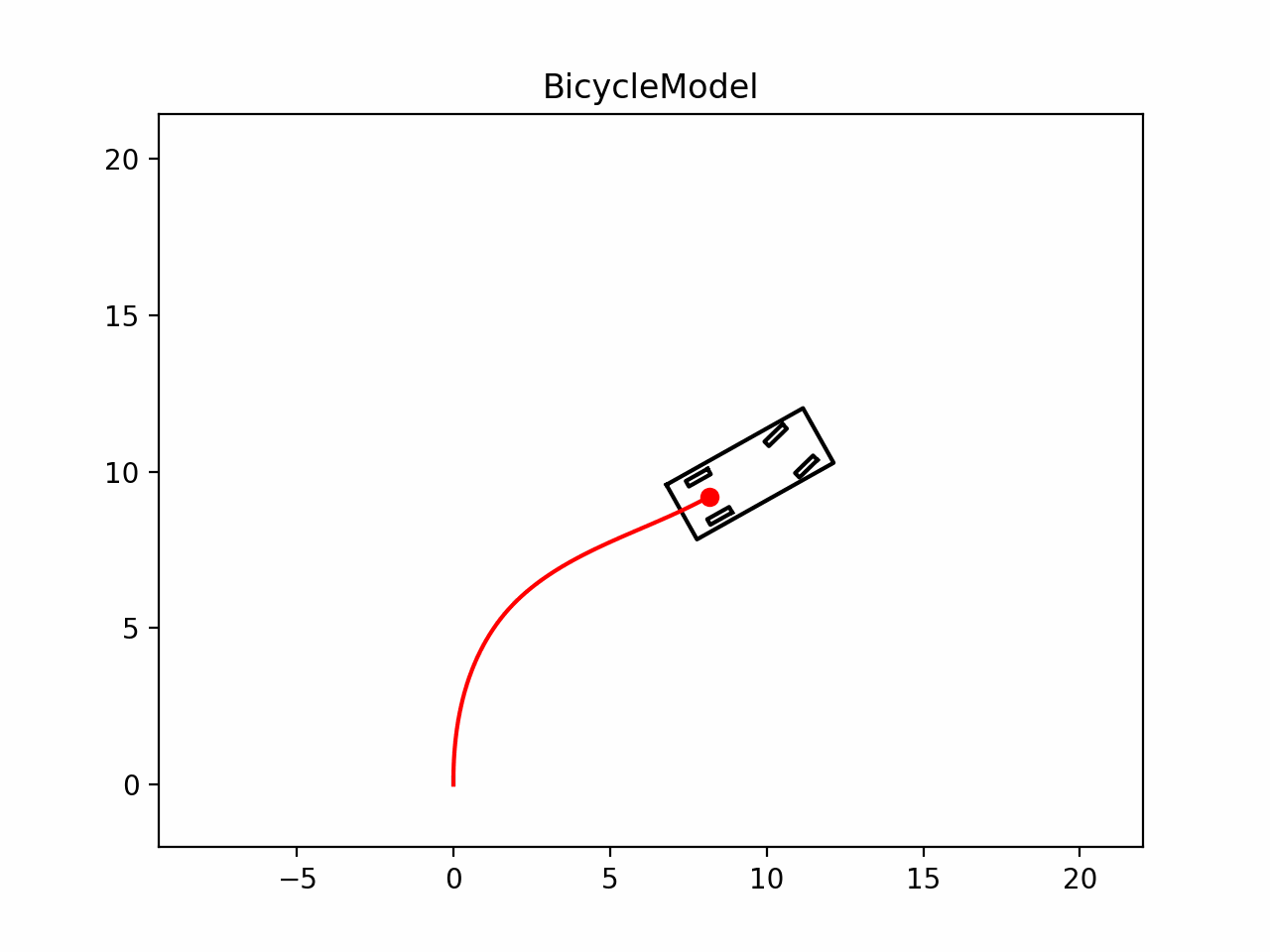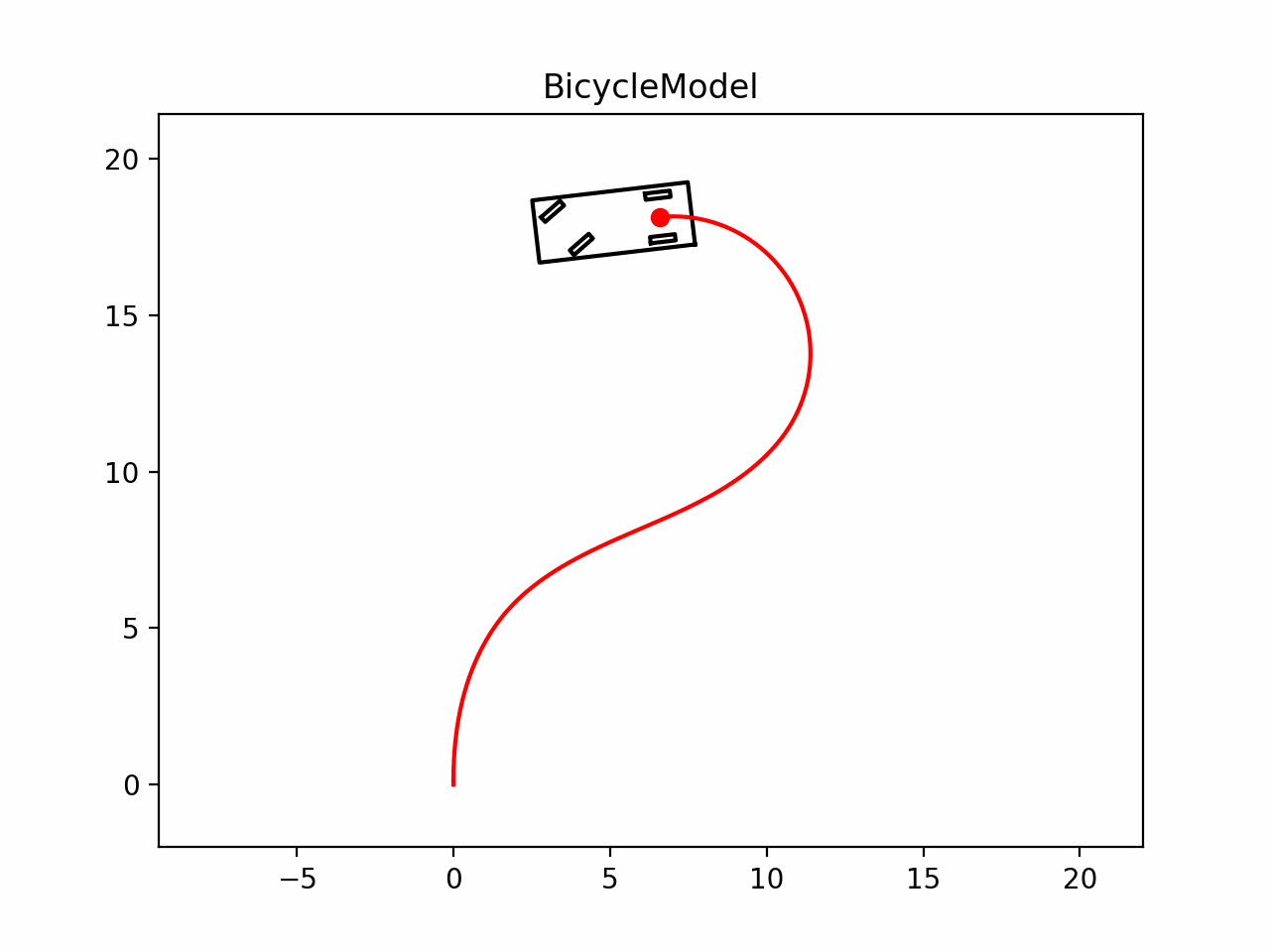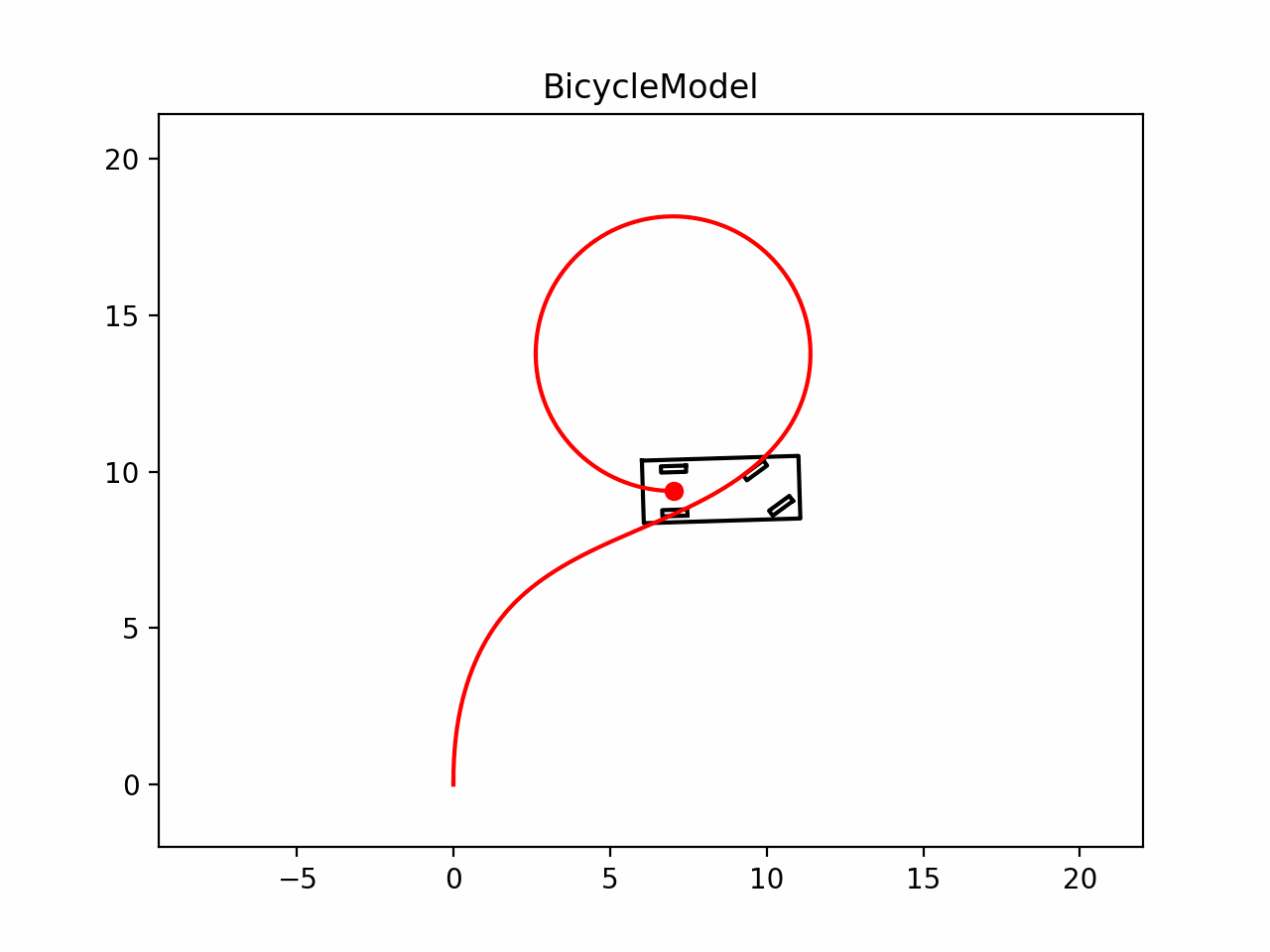
要进行轨迹规划算法,首先我们要建立运动学模型来描述车辆的运动.但是真实世界中车辆的运动是复杂的,为了描述和预测车辆在二维平面上的运动,需要对车辆的运动进行简化.运动学模型基于一系列假设，如车辆行驶速度变化缓慢、车身和悬架系统为刚性、车辆运动和转向由前轮驱动等，从而将复杂的车辆动态特性简化为更易于处理的形式.有这几种常见的运动学模型:

• 自行车模型(Bicycle Model)
• 阿克曼转向模型(Ackermann steering geometry)

我们将分两节介绍这两种模型,本节介绍自行车模型

在进行运动规划时,大部分情况为了减少计算量,我们常用自行车进行相关状态转移.自行车模型是一种简单且有效的简化方式,它基于几个基本假设:

• 车辆只有前、后两个车轮，且后轮为从动轮（即不转向）。
• 忽略车辆的垂直方向运动，只考虑二维平面内的运动。
• 车辆低速运动，此时滑移角可以忽略不计。

自行车模型将车辆的运动简化为一个两轮模型,即前转向轮和后从动轮,他们位于车辆的中轴线上.自行车模型可以基于不同的参考点(前轴中心,质心,后轴中心),规划算法一般采取后轴中心为参考点,所以我们主要介绍后轴中心的自行车模型.

1.1.1 以后轴中心为参考点的自行车模型

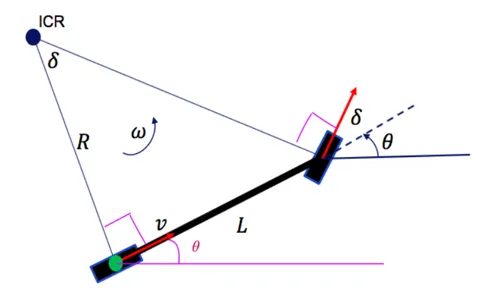
(1) 基本参数

• $v:$车辆速度。
• $(X,Y):$车辆质心位置.
• $O:$车辆瞬时转向中心.
• $R:$车辆瞬时转向半径.
• $\theta :$航向角,车辆当前位置与横坐标的夹角，即车辆的行驶方向。
• $\omega :$车辆绕瞬时转向中心旋转的角速度。
• $\delta :$前轮转角,车辆前轮相对于车辆纵轴的转角。
• $L:$轴距,前后轮之间的距离。
• $\Delta t$:时间步长

(2) 速度分解

首先，将速度v分解为横向和纵向分量:

• 横向速度分量： $v_x=v\ast cos(\theta )$
• 纵向速度分量：$v_y=v\ast sin(\theta )$

(3) 航向角变化率

航向角变化率$\dot{\theta }$,可以近似认为是角速度,于是可以推导出它的表达:

$$\begin{array}{rl}\dot{\theta }& \approx \omega \\ & =\frac{v}{R}\\ & =\frac{v}{L}\tan (\delta )\end{array}$$

(4) 状态转移方程

这样就得到了完整的状态转移方程

$$\begin{array}{rl}{x}_{r_{i+1}}& =x_{r_i}+v_{x_i}\Delta t\\ y_{r_{i+1}}& =y_{r_i}+v_{y_i}\Delta t\\ {\theta }_{i+1}& ={\theta }_i+\dot{\theta }\Delta t\approx \theta +\frac{v}{L}\tan (\delta )\Delta t\end{array}$$

1.1.2 以前轴中心的为参考点自行车模型

与后轴中心的推导类似,不在赘述. 状态转移方程:

$$\begin{array}{rl}{\dot{x}}_{f_{i+1}}& =v_{x_i}\Delta t\\ {\dot{y}}_{f_{i+1}}& =v_{y_i}\Delta t\\ \dot{\theta }& =v\ast \frac{\sin (\delta )}{L}\end{array}$$

1.1.3 以质心为参考点的自行车模型

质心的自行车模型多了一个$\beta$角,推导如下:

$$\begin{array}{rl}\tan (\beta )& =\frac{l_r}{S}\\ \beta & ={\tan }^{-1}\left(l_r\frac{\tan (\delta )}{L}\right)\end{array}$$

航向角变化率推导如下:

$$\begin{array}{rl}S& =\frac{L}{\tan (\delta )}\\ R& =\frac{S}{\cos (\beta )}\\ & =\frac{L}{\tan (\delta )\cos (\beta )}\\ \dot{\theta }& =v\ast \frac{\tan (\delta )\cos (\beta )}{L}\end{array}$$

最终完整的状态转移方程如下:

$$\begin{array}{rl}{\dot{x}}_{c_{i+1}}& =v_{x_i}\Delta t\\ {\dot{y}}_{c_{i+1}}& =v_{y_i}\Delta t\\ \dot{\theta }& =v\ast \frac{\tan (\delta )\ast cos(\beta )}{L}\\ \beta & ={\tan }^{-1}\left(l_r\frac{\tan (\delta )}{L}\right)\end{array}$$

1.1.4 有后轮转向的以质心为参考点的自行车模型

有一些车辆后轮也可以转向, 这里我们也进行状态转移推导.

(1) 基本参数

• $v:$车辆速度。
• $(X,Y):$车辆质心位置.
• $O:$车辆瞬时转向中心.
• $R:$车辆瞬时转向半径.
• $\beta :$
• $\psi :$航向角, 车辆当前位置与横坐标的夹角，即车辆的行驶方向。
• $l_f,l_r:$前悬,后悬长度
• ${\delta }_f,{\delta }_r:$前轮转角, 后轮转角

(2) 航向角变化率

$$\begin{array}{c}\frac{\sin \left({\delta }_f-\beta \right)}{{\ell }_f}=\frac{\sin \left(\frac{\pi }{2}-{\delta }_f\right)}{R}\\ \frac{\sin \left(\beta -{\delta }_r\right)}{{\ell }_r}=\frac{\sin \left(\frac{\pi }{2}+{\delta }_r\right)}{R}\end{array}$$

展开两式可得:

$$\begin{array}{c}\frac{\sin {\delta }_f\cos \beta -\sin \beta \cos {\delta }_f}{{\ell }_f}=\frac{\cos {\delta }_f}{R}\\ \frac{\cos {\delta }_r\sin \beta -\cos \beta \sin {\delta }_r}{{\ell }_r}=\frac{\cos {\delta }_r}{R}\end{array}$$

联立两式可得:

$$\begin{array}{c}(\tan {\delta }_f-\tan {\delta }_r)\cos \beta =\frac{{\ell }_f+{\ell }_r}{R}\end{array}$$

航向角变化率约等于角速度,可得:

$$\begin{array}{rl}\dot{\psi }& =\frac{v}{R}\\ & =\frac{v\cos \beta }{{\ell }_f+{\ell }_r}\left(\tan {\delta }_f-\tan {\delta }_r\right)\end{array}$$

(3) 状态转移方程

$$\begin{array}{rl}& \dot{X}=V\cos (\psi +\beta )\\ & \dot{Y}=V\sin (\psi +\beta )\\ & \dot{\psi }=\frac{V\cos \beta }{{\ell }_f+{\ell }_r}\left(\tan {\delta }_f-\tan {\delta }_r\right)\\ \beta & ={\tan }^{-1}\left(\frac{{\ell }_f\tan {\delta }_r+{\ell }_r\tan {\delta }_f}{{\ell }_f+{\ell }_r}\right)\end{array}$$

下一节, 我们会解析和运行代码.

---

🏎️自动驾驶小白说官网：https://www.helloxiaobai.cn

🐮GitHub代码仓：请前往官网获取!

🌠代码配合官网教程食用更佳！

🚀知乎，微信，知识星球全平台同号！