前面第二章数学模型有提到频域的频率特性。频率特性也是系统数学模型的一种表达形式。
频域分析法是应用频率特性研究线性系统 的一种图解方法。
目录
1. 知识梳理&逻辑图
2. 频率特性的几何表示
都是根据开环传递函数画开环特性曲线
2.1 典型环节频率特性曲线的绘制
典型环节：
比例环节频率特性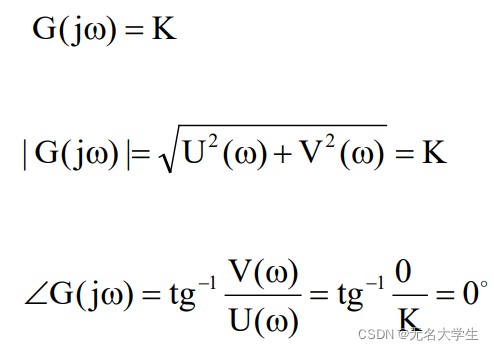
积分环节频率特性
纯微分环节频率特性
惯性环节频率特性 （低通滤波特性）：
一阶微分频率特性 （高频放大，抑制噪声能力的下降）：
振荡环节 和 二阶微分环节 频率特性较复杂，就不在这放了。
2.2 幅相频率特性曲线——Nyquist图
在极坐标复平面上画出ω值由零变化到 无穷大时的G(j ω)矢量，把矢端边成曲线。
根据G(s)写出G(jw)
将开环传递函数表示成若干典型环节的串联形式
幅频特性=组成系统的各典型环节的幅频特性之乘积。
相频特性=组成系统的各典型环节的相频特性之代数和。
绘制的时候：求A(0)、 ϕ(0)；A(∞)、 ϕ(∞)。并补充必要的特征点(如与坐标轴的交点)，根据A(ω)、 ϕ(ω) 的变化趋势，画出Nyquist图的大致形状。
举几个例子，已知系统的开环传递函数，试绘制系统的开环Nyquist图。
开环含有v个积分环节系统，Nyquist曲线起自幅角为 -v90° 的无穷远处。
2.3 对数频率特性图-Bode图
将开环传递函数表示成若干典型环节的串联形式
幅频特性=组成系统的各典型环节的对数幅频特性之代数和。
相频特性=组成系统的各典型环节的相频特性之代数和。
下表非常重要，书上P214，用这个画波特图
具体绘制方法：结合例题看即可
低频段不考虑惯性、振荡、比例微分环节
举个典型例子：
还有反过来的，给对数幅频渐近特性曲线，让确定系统的传递函数。
2.4 对数幅相曲线-尼克尔斯图
3. 频域稳定判据
3.1 奈奎斯特稳定判据（奈式判据）
奈奎斯特稳定判据的数学基础是复变函数理论中的幅角原理。
系统稳定的充要条件: 闭合曲线ΓGH逆时针包围 (-1, j0)点的圈数R等于开环传递函数的正实部极点数P。
1) N为半闭合曲线ΓGH穿越(-1, j0)点左侧负实轴的次数
2) N+ 表示正穿越的次数和（从上向下穿越）
3) N- 表示负穿越的次数和（从下向上穿越）
闭环系统正实部极点数为： Z=P-R=P-2N
更多具体内容，自己学习教材中例 5-8, 5-9
小栗子：
3.2对数频率稳定判据
奈奎斯特判据是基于复平面的半闭合曲线ΓGH判断系统 的闭环稳定性。 把曲线ΓGH转换为对数坐标下的曲线，可得对数频率稳定判据。
Nyquist图与Bode图的对应关系：
（-1, j0)点以左实轴的穿越点 ——> L(ω)>0范围内的与－180°线的穿越点。
小栗子：
4. 稳定裕度
当ΓGH穿过(-1, j0) 点时，闭环系统临界稳定。
闭合曲线ΓGH与临界点(-1, j0) 的远近程度，可用来表示闭环系统的相对稳定性。
为了使控制系统能可靠地工作，不但要求它能稳定， 而且还希望具有一定的相对稳定性。
频域的相对稳定性即稳定裕度，常用相角裕度r和幅值裕度h来度量。
稳定性裕量可以定量地确定系统离开稳定边界的远近，是评价系统稳定性好坏的性能指标，是系统 动态设计的重要依据之一。
为了得到满意的性能，相位裕度应当在30°- 60°，增益 裕度应当大于6分贝。
4.1 相位裕度\相角裕度
设系统的截止频率为 ωc，
截止频率 ωc，G(jω)H (jω) 轨迹与单位圆交点
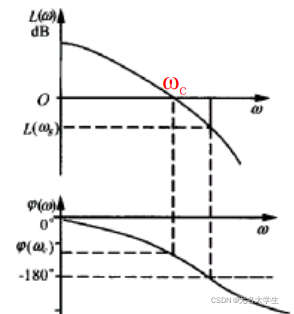截止频率 ωc， L(jω)与0分贝线 的交点。
，其实就是减&负号，负负得正
相角裕度的含义：对于闭环稳定系统，如果开环相频特性再滞后γ度，则系统将变为临界稳定。
为了使最小相位系统稳定，相位裕度必须为正。
4.2 增益裕度\幅值裕度
设系统的相位穿越频率ωx，
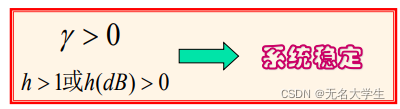
4.3 稳定裕度判断系统稳定
5. 闭环系统的频域性能指标
5.1 控制系统的频带宽度
带宽频率ωb：当闭环幅频特性下降到频率为零时的分贝值 以下3分贝时，对应的频率。
带宽（Bandwidth）定义：频率范围(0,ωb)
扫一扫
3624
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
