定积分之积分上限函数分段问题

前序.积分上限函数分段问题总结结论

1.由于 积分区间不满足”上限>下限“而分段
结论：积分上限函数要保证，这个x的范围最小值大于a，否则分段。 分段原则：中间段为x范围的最小值。（为保证“上限范围”始终大于“下限范围”）
注：如果为”积分下限函“数就先转为上限（加负号）在判断是否分段。

2.由于被积表达式在不同区间段不同，而分段。
即：f(x)在x不同范围表达式不同
正常分。（例题3）

1.解释结论（积分区间不满足分段）

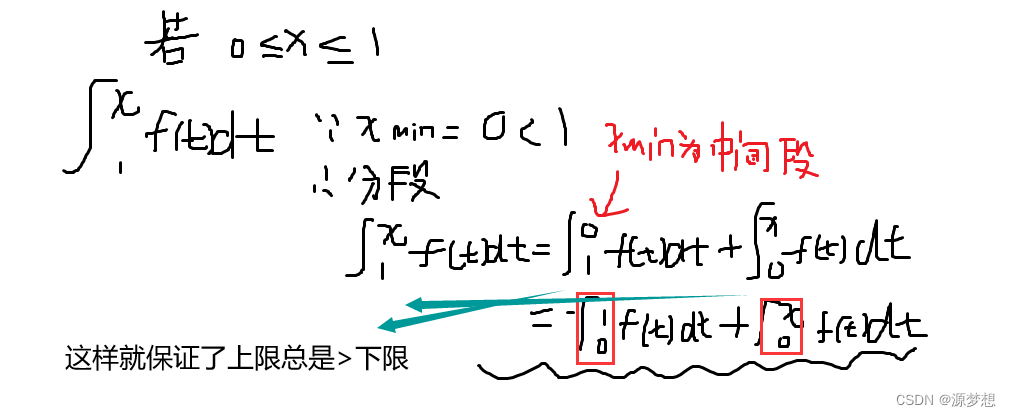
2.相关例题精选1（积分区间不满足而分段）

3.相关例题精选2（积分区间不满足而分段）

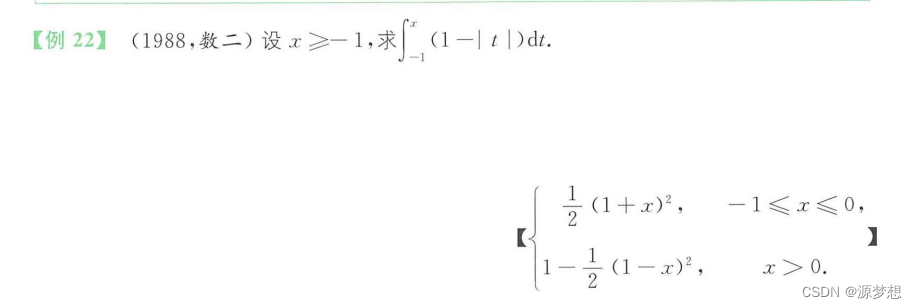
4.相关例题精选3（由于被积表达式的不同而分段）