迭代法求黎卡提（Riccati）方程的解

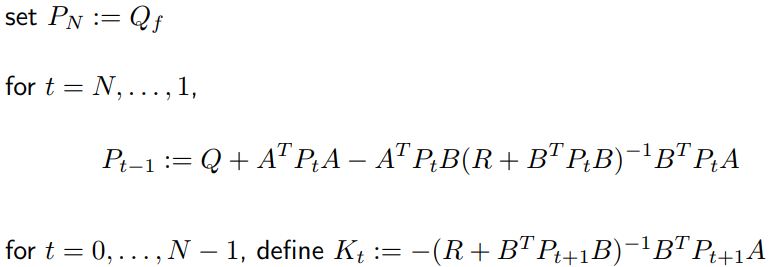
根据上述迭代法求解P，P为Riccati方程的解，然而用LQR需要计算K，再将K算出。

（迭代过程中 ，我们可以将此算法和dlqr函数求解的参数进行对比，当误差小于我们设置的允许误差我们就可以把此算法替换掉dlar函数）

P=Q
while(err > tolerance && iteration_num < max_num_iteration)
{
    iteration_num++;
    P_1 = Q + A^T*P*A - A^T*P*B(R+B^T*P*B)^(-1)*B^T*P*A;
    err = fabs(P_1 - P);
    P = P_1;
}

if(iteration_num < max_num_iteration)
{
    K = -(R + B^T * P *B)^(-1)*B^T*P*A
}