PBR理论基础1：辐射度与BRDF

Jaihk662

已于 2022-09-22 17:20:12 修改

阅读量2.7k

点赞数 1

分类专栏： # 渲染道法文章标签： PBR

于 2021-03-27 18:01:35 首次发布

本文链接：https://blog.csdn.net/Jaihk662/article/details/115263804

版权

渲染道法专栏收录该内容

8 篇文章 8 订阅

订阅专栏

前置：UnityShader9：光照基础回顾

一、反射等式(Reflection Equation)

定义：

$\mathbf{v}$ ：观察视角
$\mathbf{I}$ ：入射方向
$\mathbf{n}$ ：表面法向量

有基于物理的反射等式： $L_{o}(\mathbf{v})=\int_{\Omega} f(\mathbf{I}, \mathbf{v}) \times L_{i}(\mathbf{I})(\mathbf{n} \cdot \mathbf{I}) d \omega_{i}$ ，其为渲染方程的一个实例：其中 $L_{o}(\mathbf{v})$ 和 $L_{i}(\mathbf{I})$ 分别代表出射辐射率和入射辐射率； $f(\mathbf{I}, \mathbf{v})$ 为 BRDF 值，表示了不同方向的入射光对观察方向 $\mathbf{v}$ 的权重分布； $(\mathbf{n} \cdot \mathbf{I})$ 为表面投影结果。 $\int_{\Omega} f(w_i)d \omega_{i}$ 为极坐标半球球域积分

此函数意为：已知观察点和观察方向，可得到观察点的出射辐射率为不同方向的入射辐射率计算考虑 BRDF 叠加后的结果

辐射率：单位面积单位方向上光源的辐射通量，通常用 $L$ 表示，是一种量化光的方法，包含对颜色和亮度的评估，这在后面第二节辐射度学中也有介绍
关于 BRDF $f(\mathbf{I}, \mathbf{v})$ 的更直观理解是：当一束光沿着入射方向 $\mathbf{I}$ 到达表面某点时， $f(\mathbf{I}, \mathbf{v})$ 表示有多少部分的能量被反射到的观察方向 $\mathbf{v}$ 上，这在后面第三节中 BRDF 中也有介绍

关于精确光源(punctual light sources)

精确光源意指那些方向、大小、性质完全确定的光源，也就是之前所说的单一点光源、聚光灯、平行光这些。一个好消息是：对于游戏中的渲染，一般情况下只需要考虑这些精确光源，也就是说可以拿去反射等式中的积分部分（推导部分省略）：

$L_{o}(\mathbf{v})=\pi f\left(\mathbf{I}_{c}, \mathbf{v}\right) \times c_{l i g h t}\left(\mathbf{n} \cdot \mathbf{I}_{c}\right)$

这样对于场景中的多个光源，只需要将光源方向 $\mathbf{I}_{c}$ 和光源颜色 $c_{light}$ 代入计算后累加就好

先提反射等式是因为这是一个不错的切入点

二、辐射度学(Radiometry)

由于非相关专业研究，仅应用，所以这一块尽可能通俗易懂，就没那么细致了

能量(Energy)

这个很简单，符号 $Q$ ，单位焦耳 $J$ ，每个光子都有一定能量

功率(Power)

这个也很常见，瓦特 $W$ ，单位焦耳/秒 $J / s$ ，对于辐射率，也称作为辐射通量(Radiant Flux)，指单位时间内通过表面或者空间区域的能量的总和，符号 $\Phi$ ，定义为 $\Phi=\frac{d Q}{d t}$ ，RGB 值正是对辐射通量的描述

辐照度(Irradiance)与辐出度(Radiant Existance)

指单位时间内到达单位面积的辐射能量，也就是到达单位面积的辐射通量 $\Phi$ ，符号 $E$ ，定义为 $E=\frac{d \Phi}{d A}$ ，单位 $W / m^{2}$

辐出度和辐照度类似，不过一个是到达表面，一个是离开表面，符号为 $M$

立体角(Solid Angle)与光表示

基本上上过学的都知道弧度这个概念，立体角就可以理解为是弧度的三维扩展，符号 $w$ ，单位为立体弧度(Steradian) $sr$ ，单位球的表面积是 $4\pi$ ，所以整个球面的立体角也是 $4\pi$

可以用一个向量和一个立体角来表示一束光线，向量表示这束光线的指向，立体角表示这束光线投射在单位球上的面积，也就是光束的粗细。往往我们会对这个立体角进行微分，这就对应着前一节中的 $d \omega_{i}$ ，由此可以引申出

$\mathbf{I}$ 辐射强度(Radiant Intensity)，通过单位立体角的辐射通量，它可以用于度量通过一个点的通量的密度，符号 $I$ ，定义为 $I=\frac{d \Phi}{d \omega}$ ，单位 $W / sr$
$\mathbf{L}$ 辐射率(Radiance)：每单位面积下每单位立体角的辐射通量密度，也就是从一个微小面积表面出发，射向某个微小方向的通量，符号 $L$ ，定义为 $L=\frac{d \Phi}{d \omega d A^{\perp}}$ ，单位 $W / m^{2} s r$ ，其中 $d A^{\perp}$ 为微分面积 $dA$ 在垂直于光线方向的投影

辐射率正是我们眼睛看到的物体上对应表面的颜色，在基于物理着色时，计算表面一点的颜色也就是计算它的辐射率

三、双向反射分布函数(Bidirectional Reflectance Distribution Function)

关于 BRDF 前一节也提到过： BRDF $f(\mathbf{I}, \mathbf{v})$ 更直观理解是：当一束光沿着入射方向 $\mathbf{I}$ 到达表面某点时， $f(\mathbf{I}, \mathbf{v})$ 表示有多少部分的能量被反射到的观察方向 $\mathbf{v}$ 上。再细致一点：对于 BRDF 的全称双向反射分布函数，其中的双向指的就是 $\mathbf{v}$ 和 $\mathbf{I}$ ，可以说：当给定入射角度后，BRDF 能够给出所有出射方向上的反射和散射光线的相对分布情况；又或者是给定观察方向（即出射方向）后， BRDF 能够给出从所有入射方向到该出射方向的光线分布

假设一个平面的表面绝对光滑（比如镜面），那么对于所有的入射光线 $w_i$ （其中一束除外）而言 BRDF 函数都会返回 0，只有一束与出射光线 $w_0$ 拥有相同角度的光线会得到 1.0 这个返回值。一般情况下，只需要考虑各向同性(isotropic)的 BRDF，此时绕着表面法线旋转入射方向或观察方向并不会影响到 BRDF 的结果

基于经验 or 基于物理？

在前置章节中，已经提到过了一些基于经验的 BRDF，对于基于物理的 BRDF，需要满足以下两个条件：

交换律： $f(\mathbf{I}, \mathbf{v})=f(\mathbf{v}, \mathbf{I})$
反射能量 ≤ 入射光能： $\forall \mathbf{I}, \int_{\Omega} f(\mathbf{I}, \mathbf{v})(\mathbf{n} \cdot \mathbf{I}) d \omega_{o} \leqslant 1$

BRDF 的本质

了解了上一节部分辐射度学的内容后，各向同性的 BRDF 的推导就相对容易了：

可以得到表面（观察点）反射到 $\mathbf{v}$ 方向的反射光的微分辐射率为 $d L_{o}(v)$ ，这仅考虑了特定的光源方向 $\mathbf{I}$ ，以及次表面上来自入射光方向 $\mathbf{I}$ 的微分辐照度 $d E(l)$

那么就有 BRDF： $f(\mathbf{I}, \mathbf{v})=\frac{d L_{o}(v)}{d E(l)}$

表面对不同频率的光反射率可能不一样，因此BRDF和光的频率有关，图形学中将BRDF表示为RGB向量，三个分量各有自己的 BRDF 函数。不过这里可以暂时不考虑的那么细致

有些地方会将第 $i$ 个光源的光源方向 $\mathbf{I}$ 表示为表面与立体角 $\left(p, \omega_{1}\right)$ ，将观察方向 $\mathbf{v}$ 表示为表面与反射立体角 $\left(p, \omega_{o}\right)$ ，这样描述下的 BRDF 就为

$f_{r}\left(p, \omega_{o}, \omega_{i}\right)=\frac{d L_{o}\left(p, \omega_{o}\right)}{d E\left(p, \omega_{i}\right)}$

BRDF 与反射等式

根据上面的内容，可以很轻松的得出：观察点表面 $p$ 的辐照度 $E$ 为所有入射辐射率计算叠加后的结果，也就是 $E(p)=\int_{\Omega} L_{i}(p, \omega) (\mathbf{n} \cdot \mathbf{I})d \omega=\int_{\Omega} L_{i}(p, \omega) \cos \theta_{i} d \omega$ ，至于这个 $\cos \theta_{i}$ 的来源，正是 $d A^{\perp}$ 到 $dA$ 的转换产生

考虑到表面 $p$ 的辐照度正是半球上任一光线 $w_i$ 的辐射率积分，就有 $d E\left(p, \omega_{i}\right)=L_{i}\left(p, \omega_{i}\right) \cos \theta_{i} d \omega_{i}$

代入到 BRDF 中，可以得到： $f_{r}\left(p, \omega_{o}, \omega_{i}\right)=\frac{d L_{o}\left(p, \omega_{o}\right)}{d E\left(p, \omega_{i}\right)}=\frac{d L_{o}\left(p, \omega_{o}\right)}{L_{i}\left(p, \omega_{i}\right) \cos \theta_{i} d \omega_{i}}$

此时 BRDF 乘上辐射率，就可以得到前面的反射等式： $L_{o}\left(p, \omega_{o}\right)=\int_{\Omega} f_{r}\left(p, \omega_{i}, \omega_{o}\right) L_{i}\left(p, \omega_{i}\right) \cos \theta_{i} d \omega_{i}$ ，完美！

当然了，这上面的定义是不能直接拿来计算表面反射辐射率的，还需要建立一个能模拟真实光照的模型，这个就不在这一章讲了

四、扩展(Extra)

1)：辐照度的衰减与间距

前面提到过辐照度就是指单位时间内到达单位面积的辐射能量，也就是到达单位面积的辐射通量 $\Phi$ ，符号 $E$ ，定义为 $E=\frac{d \Phi}{d A}$ ，单位 $W / m^{2}$ ，而无论是辐照度还是辐出度都被称为辐射通量密度(Radiant Flux Density)

处理通量密度时还需要考虑到表面朝向和光线方向的角度，假设照射到表面时，光线间距为 $d$ ，那么根据下图就可以得到：当且仅当光线垂直表面照射时，通量密度最大，当光线倾斜照射表面时，间距就变为 $\frac{d }{\cos \theta}$ ，此时间距变大通量密度降低，定义 $E_{L}=\frac{d\Phi}{dA^{\perp}}=\frac{d\Phi}{dA \frac{1}{\cos \theta_{i}}}$

季节的变化正是这个原理：光照角度越来越大，从而导致通量密度降低，辐照度降低

除了角度，还有距离，假设有这样的一个场景：有两个个球包住了一个点光源，从内到外分别为 AB，它们的圆心正是点光源的中心，这样点亮光源后穿过球 A 和球 B 的辐射通量必然是相同的 $\Phi$ ，而它们的面积却不相同。因此可以得出：通量密度与距离的平方成反比，离光源越远，通量密度越低，这也是光照衰减的本质，此时通量密度 $E=\frac{\Phi}{4 \pi r^{2}}$

2)：完整的渲染方程

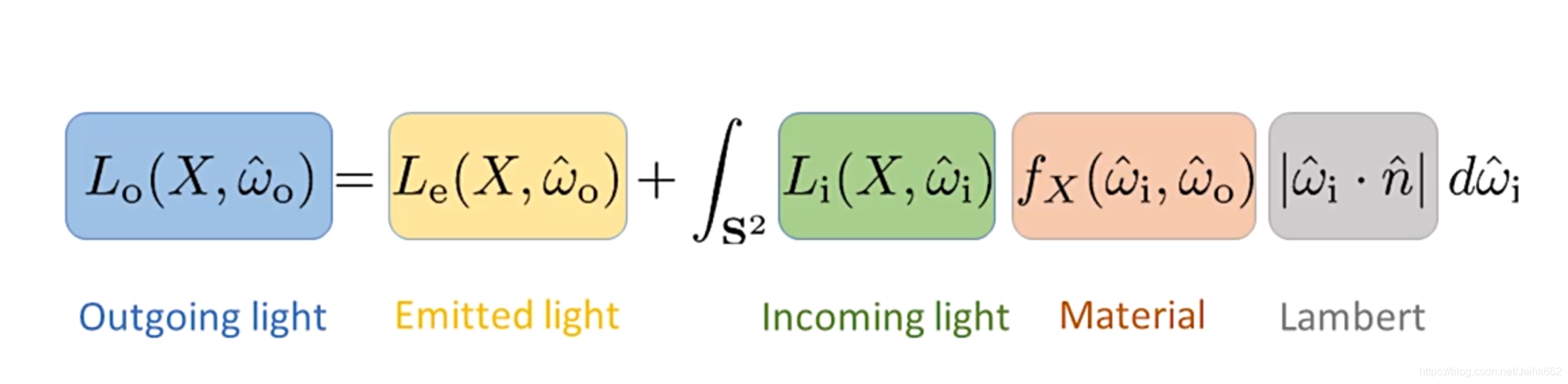
参考：

Jaihk662

关注

1
点赞
踩
7

收藏

觉得还不错? 一键收藏
0
评论
PBR理论基础1：辐射度与BRDF

前置：UnityShader9：光照基础回顾一、反射等式(reflection equation)定义：：观察视角：入射方向：表面法向量有基于物理的反射等式：，其为渲染方程的一个实例其中和分别代表出射辐射率和入射辐射率，为圆域积分...
复制链接

扫一扫