参考:
[1] 张振虎博客DDIM
[2] https://www.bilibili.com/video/BV1Ra4y1F73C/?spm_id_from=333.337.search-card.all.click
1 DDPM简单回顾
DDPM的核心思想是构建一个马尔可夫链式结构,逐步往 x 0 x_0 x0添加不同强度的高斯噪声,令其最终变成标准正态分布,这个过程又叫扩散过程。逆向阶段是降噪的过程,目的是为了估计降噪转换核 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p(xt−1∣xt),就可以从一个正态分布的高斯噪声 x T x_T xT逐步降噪生成近似于真实图像数据的概率分布,就可以去采样生成一张新图像了。
整个网络的概率分布可以由
p
(
x
0
:
T
)
p(x_{0:T})
p(x0:T)表示,根据链式法则,扩散过程可以表示为:
p
(
x
0
:
T
)
=
q
(
x
0
)
∏
t
=
1
T
q
(
x
t
∣
x
t
−
1
)
p(x_{0:T})=q(x_0)\prod_{t=1}^T q(x_t|x_{t-1})
p(x0:T)=q(x0)t=1∏Tq(xt∣xt−1)
前向扩散过程的转换核
p
(
x
t
∣
x
t
−
1
)
p(x_t|x_{t-1})
p(xt∣xt−1)是线性高斯转换,概率密度为
p
(
x
t
∣
x
t
−
1
)
=
N
(
α
t
x
t
−
1
,
1
−
α
t
I
)
p(x_t|x_{t-1}) = N(\sqrt{\alpha_t}x_{t-1},\sqrt{1-\alpha_t}I)
p(xt∣xt−1)=N(αtxt−1,1−αtI)
既在
x
t
−
1
x_{t-1}
xt−1的基础上添加高斯噪声得到
x
t
x_t
xt,高斯噪声的均值为0,方差为
1
−
α
t
1-\alpha_t
1−αt。再利用条件高斯概率的计算技巧,可以得到
q
(
x
t
∣
x
0
)
=
N
(
α
ˉ
t
x
0
,
1
−
α
t
ϵ
)
q(x_t|x_0) = N(\sqrt{\bar\alpha_t}x_0,\sqrt{1-\alpha_t}\epsilon)
q(xt∣x0)=N(αˉtx0,1−αtϵ)
逆向过程的联合概率可以表示为
p
(
x
0
:
T
)
=
p
(
x
T
)
∏
t
=
1
T
p
(
x
t
−
1
∣
x
t
)
p(x_{0:T})=p(x_T)\prod_{t=1}^Tp(x_{t-1}|x_t)
p(x0:T)=p(xT)t=1∏Tp(xt−1∣xt)
我们的主要目标就是估计降噪的转换核
p
(
x
t
−
1
∣
x
t
)
p(x_{t-1}|x_t)
p(xt−1∣xt)的近似表示,根据似然最大理论,我们要极大化观测数据
x
0
x_0
x0的对数似然(
x
1
:
T
x_{1:T}
x1:T均为隐变量),既
l
o
g
p
(
x
0
)
=
l
o
g
∫
p
(
x
0
:
T
)
d
x
1
:
T
log\space p(x_0) = log\int p(x_{0:T})dx_{1:T}
log p(x0)=log∫p(x0:T)dx1:T
但正是因为隐变量的积分形式,导致无法直接极大化对数似然。但可以利用詹森不等式对该形式进行等价替换,既
E
q
(
x
0
)
[
l
o
g
p
(
x
0
)
]
≥
E
q
(
x
1
:
T
∣
x
0
)
[
l
o
g
p
(
x
0
:
T
)
q
(
x
1
:
T
∣
x
0
)
]
⇒
E
q
(
x
1
∣
x
0
)
[
l
o
g
p
θ
(
x
0
∣
x
1
)
]
−
∑
t
=
2
T
E
q
(
x
t
∣
x
0
)
[
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
]
\begin{aligned} E_{q(x_0)}[log\space p(x_0)]&\ge E_{q(x_{1:T}|x_0)}[log\frac{p(x_{0:T)}}{q(x_{1:T}|x_0)}]\\ &\Rightarrow E_{q(x_1|x_0)}[log p_\theta(x_0|x_1)]-\sum_{t=2}^T E_{q(x_t|x_0)}[KL(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)] \end{aligned}
Eq(x0)[log p(x0)]≥Eq(x1:T∣x0)[logq(x1:T∣x0)p(x0:T)]⇒Eq(x1∣x0)[logpθ(x0∣x1)]−t=2∑TEq(xt∣x0)[KL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt)]
代入各项之后可以得到最终的优化目标是一个均方误差,既
L
:
=
∑
t
=
1
T
C
E
q
(
x
t
∣
x
0
)
[
∣
∣
ϵ
t
−
ϵ
^
θ
(
x
t
,
t
)
∣
∣
2
]
L := \sum_{t=1}^TC E_{q(x_t|x_0)}[|| \epsilon_t-\hat\epsilon_\theta(x_t,t)||^2]
L:=t=1∑TCEq(xt∣x0)[∣∣ϵt−ϵ^θ(xt,t)∣∣2]
2 DDIM解决了什么
2.1 DDPM的问题和可能解决方法
众所周知,DDPM的一个缺点就是其采样生成的过程十分缓慢,明显且主要的一个原因就是,降噪采样过程的TimeSteps通常是非常大的,在DDPM原论文中, T = 1000 T=1000 T=1000。而降噪过程是一步一步降噪的。那么
(1) 是否能令
T
T
T更小一些?
答: 不可以。 由DDPM可知,
x
t
=
α
t
x
t
−
1
+
1
−
α
t
ϵ
,
ϵ
∼
N
(
0
,
1
)
x
t
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
,
ϵ
∼
N
(
0
,
1
)
x_t = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}\epsilon, \epsilon\sim N(0,1)\\ x_t = \sqrt{\bar\alpha_t}x_{0}+\sqrt{1-\bar\alpha_t}\epsilon, \epsilon\sim N(0,1)
xt=αtxt−1+1−αtϵ,ϵ∼N(0,1)xt=αˉtx0+1−αˉtϵ,ϵ∼N(0,1)
而
β
\beta
β的值介于(0.02,0.0001)之间,随着
t
t
t增大,
β
1
<
β
2
<
.
.
.
<
β
t
\beta_1<\beta_2<...<\beta_t
β1<β2<...<βt,也就是
α
1
>
.
.
.
>
α
t
\alpha_1>...>\alpha_t
α1>...>αt,也就是
t
t
t越大,
α
ˉ
t
\bar\alpha_t
αˉt越小(因为
α
\alpha
α都小于1)
也就是说,只有
t
t
t非常大的时候,
α
ˉ
t
\sqrt{\bar\alpha_t}
αˉt才能非常小,
1
−
α
ˉ
t
\sqrt{1-\bar\alpha_t}
1−αˉt才能接近于1,我们得到的
x
t
x_t
xt才能近似于
ϵ
∼
N
(
0
,
1
)
\epsilon \sim N(0,1)
ϵ∼N(0,1)。 所以不可以。
(2) 是否能跳步采样呢?
答: 同样也不可以,我们的模型的最终要拟合的概率分布
p
(
x
t
−
1
∣
x
t
,
x
0
)
=
p
(
x
t
∣
x
t
−
1
,
x
0
)
p
(
x
t
−
1
∣
x
0
)
p
(
x
t
∣
x
0
)
p(x_{t-1}|x_t,x_0)=\frac{p(x_t|x_{t-1},x_0)p(x_{t-1}|x_0)}{p(x_t|x_0)}
p(xt−1∣xt,x0)=p(xt∣x0)p(xt∣xt−1,x0)p(xt−1∣x0)
都是基于马尔科夫链才得到的,如果我们跳步采样,那就是不遵循马尔科夫过程,那么以上公式也就不成立。
ps. 为什么说我们的最终目标是拟合上边这个后验分布呢?我们的模型不是输出噪声吗?我们的模型输出噪声 ϵ θ \epsilon_\theta ϵθ,随后我们会根据 x ^ 0 = x t − 1 − α ˉ t ϵ θ α ˉ t \hat x_0 = \frac{x_t-\sqrt{1-\bar\alpha_t}\epsilon_\theta}{\sqrt{\bar\alpha_t}} x^0=αˉtxt−1−αˉtϵθ的式子去得到 x ^ 0 \hat x_0 x^0,然后我们根据 p ( x t − 1 ∣ x t , x 0 ) p(x_{t-1}|x_t,x_0) p(xt−1∣xt,x0)的均值公式代入 x t , x ^ 0 x_t,\hat x_0 xt,x^0去计算出 μ θ \mu_\theta μθ,我们这个 μ θ \mu_\theta μθ才是模型的输出,也就是该概率分布的期望。
2.2 去马尔可夫过程
再来看
p
(
x
t
−
1
∣
x
t
,
x
0
)
p(x_{t-1}|x_t,x_0)
p(xt−1∣xt,x0),我们需要知道前提条件
x
0
x_0
x0和
x
t
x_t
xt,而
x
0
x_0
x0是我们的观测数据,
x
t
x_t
xt可以由
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)得到,所以说
x
t
x_t
xt也不依赖于
x
t
−
1
x_{t-1}
xt−1。那么
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)是如何得来的呢?它是由联合概率的边际化得到的,也就是:
q
(
x
t
∣
x
0
)
=
∫
q
(
x
1
:
t
∣
x
0
)
d
x
1
:
t
−
1
q(x_t|x_0)=\int q(x_{1:t}|x_0)dx_{1:t-1}
q(xt∣x0)=∫q(x1:t∣x0)dx1:t−1
在DDPM论文中,对其分解是利用马尔科夫链的形式分解的,但无论如何分解,最终都是将积分形式去掉,还有很多种不同的分解方法,但无论如何分解,最终的
q
(
x
t
∣
x
0
)
q(x_t|x_0)
q(xt∣x0)的结构都是一样的,所以前向过程的马尔科夫链不是必须的。
我们只要保持 p ( x t − 1 ∣ x t , x 0 ) p(x_{t-1}|x_t,x_0) p(xt−1∣xt,x0)和 q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0)的形式和DDPM保持一致,我们就可以构建一个非马尔可夫链的DDPM等价模型,也就可以实现跳步采样操作了。
以下为正式推导过程
我们可以设
s
≤
k
−
1
s\le k-1
s≤k−1(如果
s
=
k
−
1
s=k-1
s=k−1的话实际上就相当于
t
,
t
−
1
t,t-1
t,t−1了),为了保持形式不变,我们有:
p
(
x
s
∣
x
k
,
x
0
)
=
p
(
x
k
∣
x
s
,
x
0
)
p
(
x
s
∣
x
0
)
p
(
x
k
∣
x
0
)
p(x_s|x_k,x_0)=\frac{p(x_k|x_s,x_0)p(x_s|x_0)}{p(x_k|x_0)}
p(xs∣xk,x0)=p(xk∣x0)p(xk∣xs,x0)p(xs∣x0)
且已知DDPM中,
p
(
x
t
−
1
∣
x
t
,
x
0
)
p(x_{t-1}|x_t,x_0)
p(xt−1∣xt,x0)的均值和
x
t
,
x
0
x_t,x_0
xt,x0有关,所以我们可以设
p
(
x
s
∣
x
k
,
x
0
)
=
N
(
x
s
;
k
x
0
+
m
x
k
,
σ
2
I
)
p(x_s|x_k,x_0) = N(x_s; kx_0+mx_k, \sigma^2I)
p(xs∣xk,x0)=N(xs;kx0+mxk,σ2I)
其中
k
,
m
,
σ
k,m,\sigma
k,m,σ均为未知量。对于非马尔可夫过程,
p
(
x
t
∣
x
0
)
p(x_t|x_0)
p(xt∣x0)也是成立的。所以有:
x
s
=
k
x
0
+
m
x
k
+
σ
ϵ
1
=
k
x
0
+
m
(
α
ˉ
k
x
0
+
1
−
α
ˉ
k
ϵ
2
)
+
σ
ϵ
1
=
(
k
+
m
α
ˉ
k
)
x
0
+
m
1
−
α
ˉ
k
ϵ
2
+
σ
ϵ
1
=
(
k
+
m
α
ˉ
k
)
x
0
+
m
2
(
1
−
α
ˉ
k
)
+
σ
2
ϵ
=
α
ˉ
s
x
0
+
1
−
α
ˉ
s
ϵ
\begin{aligned} x_s &= kx_0+mx_k+\sigma\epsilon_1\\ &= kx_0+m(\sqrt{\bar\alpha_k}x_0+\sqrt{1-\bar\alpha_k}\epsilon_2)+\sigma\epsilon_1\\ &=(k+m\sqrt{\bar\alpha_k})x_0 + m\sqrt{1-\bar\alpha_k}\epsilon_2+\sigma\epsilon_1\\ &=(k+m\sqrt{\bar\alpha_k})x_0 +\sqrt{m^2(1-\bar\alpha_k)+\sigma^2}\epsilon\\ &= \sqrt{\bar\alpha_s}x_0 + \sqrt{1-\bar\alpha_s}\epsilon \end{aligned}
xs=kx0+mxk+σϵ1=kx0+m(αˉkx0+1−αˉkϵ2)+σϵ1=(k+mαˉk)x0+m1−αˉkϵ2+σϵ1=(k+mαˉk)x0+m2(1−αˉk)+σ2ϵ=αˉsx0+1−αˉsϵ
所以我们可以得到:
m
=
1
−
α
ˉ
s
−
σ
2
1
−
α
ˉ
k
k
=
α
ˉ
s
−
α
ˉ
k
(
1
−
α
ˉ
s
−
σ
2
)
1
−
α
ˉ
k
\begin{aligned} m &= \sqrt{\frac{1-\bar\alpha_s-\sigma^2}{1-\bar\alpha_k}}\\ k &= \sqrt{\bar\alpha_s}-\sqrt{\frac{\bar\alpha_k(1-\bar\alpha_s-\sigma^2)}{1-\bar\alpha_k}} \end{aligned}
mk=1−αˉk1−αˉs−σ2=αˉs−1−αˉkαˉk(1−αˉs−σ2)
将其代入到
μ
p
=
k
x
0
+
m
x
k
\mu_p = kx_0+mx_k
μp=kx0+mxk,得
μ
p
=
α
ˉ
s
x
0
+
1
−
α
ˉ
s
−
σ
2
1
−
α
ˉ
k
(
x
k
−
α
ˉ
k
x
0
)
\mu_p = \sqrt{\bar\alpha_s}x_0+\sqrt{\frac{1-\bar\alpha_s-\sigma^2}{1-\bar\alpha_k}}(x_k-\sqrt{\bar\alpha_k}x_0)
μp=αˉsx0+1−αˉk1−αˉs−σ2(xk−αˉkx0)
所以我们最终得到非马尔可夫链的后验分布
p
(
x
s
∣
x
k
,
x
0
)
∼
N
(
α
ˉ
s
x
0
+
1
−
α
ˉ
s
−
σ
2
1
−
α
ˉ
k
(
x
k
−
α
ˉ
k
x
0
)
,
σ
2
I
)
p(x_s|x_k,x_0)\sim N( \sqrt{\bar\alpha_s}x_0+\sqrt{\frac{1-\bar\alpha_s-\sigma^2}{1-\bar\alpha_k}}(x_k-\sqrt{\bar\alpha_k}x_0),\sigma^2 I)
p(xs∣xk,x0)∼N(αˉsx0+1−αˉk1−αˉs−σ2(xk−αˉkx0),σ2I)
同样,我们将
x
^
0
=
x
k
−
1
−
α
ˉ
k
ϵ
^
k
(
x
k
,
k
)
α
ˉ
k
\hat x_0=\frac{x_k -\sqrt{1-\bar\alpha_k}\hat\epsilon_k(x_k,k)}{\sqrt{\bar\alpha_k}}
x^0=αˉkxk−1−αˉkϵ^k(xk,k)代入上式,我们可以得到
x
s
x_s
xs的采样公式:
x
s
=
α
ˉ
s
x
0
+
1
−
α
ˉ
s
−
σ
2
x
k
−
α
ˉ
k
x
0
1
−
α
ˉ
k
+
σ
ϵ
k
∗
=
α
ˉ
s
(
x
k
−
1
−
α
ˉ
k
ϵ
^
k
(
x
k
,
k
)
α
ˉ
k
)
+
1
−
α
ˉ
s
−
σ
2
ϵ
^
k
+
σ
ϵ
k
∗
\begin{aligned} x_s &= \sqrt{\bar\alpha_s}x_0+\sqrt{1-\bar\alpha_s-\sigma^2}\frac{x_k-\sqrt{\bar\alpha_k}x_0}{\sqrt{1-\bar\alpha_k}}+\sigma\epsilon_k^*\\ &= \sqrt{\bar\alpha_s}(\frac{x_k -\sqrt{1-\bar\alpha_k}\hat\epsilon_k(x_k,k)}{\sqrt{\bar\alpha_k}})+\sqrt{1-\bar\alpha_s-\sigma^2}\hat\epsilon_k+\sigma\epsilon_k^* \end{aligned}
xs=αˉsx0+1−αˉs−σ21−αˉkxk−αˉkx0+σϵk∗=αˉs(αˉkxk−1−αˉkϵ^k(xk,k))+1−αˉs−σ2ϵ^k+σϵk∗
其中
ϵ
^
k
\hat\epsilon_k
ϵ^k为预测的噪声,
ϵ
k
∗
\epsilon_k^*
ϵk∗为随机采样的标准高斯噪声。又或者符号变为以下:
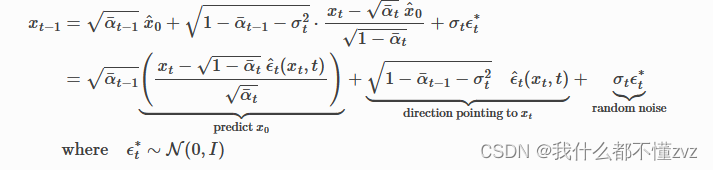
2.3 标准差的选取
当标准差设为 σ 2 = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t \sigma^2 = \frac{(1-\alpha_t)(1-\bar\alpha_{t-1})}{1-\bar\alpha_t} σ2=1−αˉt(1−αt)(1−αˉt−1) (DDPM的形式)
这时DDIM就退化为了DDPM,推导公式如下:

可见DDPM的期望和DDIM的期望一致,所以说DDPM是DDIM的特例。
当标准差设为 σ 2 = 0 \sigma^2 =0 σ2=0
直观来说,就是采样公式的随机噪声项 σ ϵ k ∗ \sigma\epsilon_k^* σϵk∗没了,相当于 x s x_s xs等于 p ( x s ∣ x k , x 0 ) p(x_s|x_k,x_0) p(xs∣xk,x0)的期望。这意味着:
- x s x_s xs不再是从 p ( x s ∣ x k , x 0 ) p(x_s|x_k,x_0) p(xs∣xk,x0)随机采样,而是采样其均值,又其满足高斯分布,也就是采样概率密度分布的最高点,也就是最大概率的采样点。
- 没有了随机噪声项,整个式子也就变成了确定性等式计算。
那么它是如何加速采样的呢?(以下是从随机性的直观角度,论文是从子序列角度)
方差不为0,相当于 x t x_t xt到 x t − 1 x_{t-1} xt−1的每一步都是随机采样,随机性不可控,会走很多弯路,相当于从 x T x_T xT到 x 0 x_0 x0,虽然目的地方向(期望)是确定的,但是总是在该方向上加上一点随机噪声,自然到达 x 0 x_0 x0的步长会大一些。
方差为0时,笔直地沿着期望的方向走,自然就更快了。
基于分数的生成模型,分数等价于
p
(
x
t
)
p(x_t)
p(xt)的梯度,既沿着
p
(
x
0
)
p(x_0)
p(x0)的方向。我们可以知道梯度和噪声之间的关系:
∇
l
o
g
p
(
x
t
)
=
−
1
1
−
α
ˉ
t
ϵ
^
t
(
x
t
,
t
)
\nabla log\space p(x_t) = -\frac{1}{\sqrt{1-\bar\alpha_t}}\hat\epsilon_t(x_t,t)
∇log p(xt)=−1−αˉt1ϵ^t(xt,t)
所以
x
^
0
\hat x_0
x^0可以用该公式替代掉噪声:
x
^
0
=
x
k
+
(
1
−
α
ˉ
k
)
∇
l
o
g
p
(
x
k
)
α
ˉ
k
\hat x_0=\frac{x_k +(1-\bar\alpha_k)\nabla log p(x_k)}{\sqrt{\bar\alpha_k}}
x^0=αˉkxk+(1−αˉk)∇logp(xk)
再将这一项代入
x
s
x_s
xs的采样公式里
x
s
=
α
ˉ
s
x
^
0
+
1
−
α
ˉ
s
−
σ
2
x
k
−
α
ˉ
k
x
^
0
1
−
α
ˉ
k
+
σ
ϵ
k
∗
=
α
ˉ
s
x
k
+
(
1
−
α
ˉ
k
)
∇
l
o
g
p
(
x
k
)
α
ˉ
k
+
1
−
α
ˉ
s
−
σ
2
[
x
k
+
α
ˉ
k
(
x
k
+
(
1
−
α
ˉ
k
)
∇
l
o
g
p
(
x
k
)
α
ˉ
k
)
]
+
σ
ϵ
k
∗
=
.
.
.
(
懒得推了)
=
α
ˉ
s
α
ˉ
k
x
k
+
(
α
ˉ
s
α
ˉ
k
(
1
−
α
ˉ
k
)
−
1
−
α
ˉ
s
−
σ
2
α
ˉ
k
)
∇
l
o
g
p
(
x
k
)
+
σ
ϵ
k
∗
:
=
A
x
k
+
B
∇
l
o
g
p
(
x
k
)
+
σ
ϵ
k
∗
\begin{aligned} x_s &= \sqrt{\bar\alpha_s}\hat x_0 +\sqrt{1-\bar\alpha_s-\sigma^2}\frac{x_k-\sqrt{\bar\alpha_k}\hat x_0}{\sqrt{1-\bar\alpha_k}}+\sigma\epsilon_k^*\\ &= \sqrt{\bar\alpha_s}\frac{x_k +(1-\bar\alpha_k)\nabla log p(x_k)}{\sqrt{\bar\alpha_k}}\\ &+ \sqrt{1-\bar\alpha_s-\sigma^2}[x_k +\sqrt{\bar\alpha_k}(\frac{x_k+(1-\bar\alpha_k)\nabla log p(x_k)}{\sqrt{\bar\alpha_k}})] +\sigma\epsilon_k^*\\ &= ...(懒得推了)\\ &= \sqrt{\frac{\bar\alpha_s}{\bar\alpha_k}}x_k +(\sqrt{\frac{\bar\alpha_s}{\bar\alpha_k}}(1-\bar\alpha_k)-\sqrt{1-\bar\alpha_s-\sigma^2}\bar\alpha_k)\nabla log p(x_k) +\sigma\epsilon_k^* \\&:= Ax_k +B\nabla logp(x_k)+\sigma\epsilon_k^* \end{aligned}
xs=αˉsx^0+1−αˉs−σ21−αˉkxk−αˉkx^0+σϵk∗=αˉsαˉkxk+(1−αˉk)∇logp(xk)+1−αˉs−σ2[xk+αˉk(αˉkxk+(1−αˉk)∇logp(xk))]+σϵk∗=...(懒得推了)=αˉkαˉsxk+(αˉkαˉs(1−αˉk)−1−αˉs−σ2αˉk)∇logp(xk)+σϵk∗:=Axk+B∇logp(xk)+σϵk∗
这就是梯度下降,
σ
=
0
\sigma=0
σ=0,则收敛速度变快

3 小结(不同的地方)
- 采样间距:采样间距可以设置为间隔50步采样等;
- 采样公式:
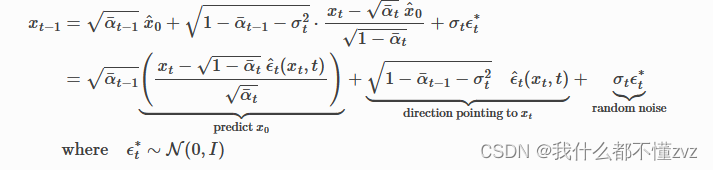






















 6281
6281











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








