【opencv机器学习】SVM 初探

最新推荐文章于 2024-08-23 00:54:06 发布

苏源流

最新推荐文章于 2024-08-23 00:54:06 发布

阅读量1.2k

点赞数

分类专栏：机器学习计算机视觉，图像处理文章标签：机器学习 svm opencv 计算机视觉支持向量机

本文链接：https://blog.csdn.net/KYJL888/article/details/69950659

版权

计算机视觉，图像处理同时被 2 个专栏收录

78 篇文章 34 订阅

订阅专栏

机器学习

8 篇文章 0 订阅

订阅专栏

1 学习参考

支持向量机(SVM)介绍

网址参考 http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/ml/introduction_to_svm/introduction_to_svm.html

支持向量机对线性不可分数据的处理

网址参考 http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/ml/non_linear_svms/non_linear_svms.html#nonlinearsvms

支持向量机(SVM)介绍

目标

本文档尝试解答如下问题:

如何使用OpenCV函数 CvSVM::train 训练一个SVM分类器，以及用 CvSVM::predict 测试训练结果。

什么是支持向量机(SVM)?

支持向量机 (SVM) 是一个类分类器，正式的定义是一个能够将不同类样本在样本空间分隔的超平面。换句话说，给定一些标记(label)好的训练样本 (监督式学习), SVM算法输出一个最优化的分隔超平面。

如何来界定一个超平面是不是最优的呢? 考虑如下问题：

假设给定一些分属于两类的2维点，这些点可以通过直线分割，我们要找到一条最优的分割线.

Note

在这个示例中，我们考虑卡迪尔平面内的点与线，而不是高维的向量与超平面。这一简化是为了让我们以更加直觉的方式建立起对SVM概念的理解，但是其基本的原理同样适用于更高维的样本分类情形。

在上面的图中，你可以直觉的观察到有多种可能的直线可以将样本分开。那是不是某条直线比其他的更加合适呢? 我们可以凭直觉来定义一条评价直线好坏的标准:

距离样本太近的直线不是最优的，因为这样的直线对噪声敏感度高，泛化性较差。因此我们的目标是找到一条直线，离所有点的距离最远。

由此， SVM算法的实质是找出一个能够将某个值最大化的超平面，这个值就是超平面离所有训练样本的最小距离。这个最小距离用SVM术语来说叫做 间隔(margin) 。概括一下，最优分割超平面 最大化 训练数据的间隔。

如何计算最优超平面?

下面的公式定义了超平面的表达式:

$f(x) = \beta_{0} + \beta^{T} x,$

$\beta$ 叫做 权重向量 ， $\beta_{0}$ 叫做 偏置(bias) 。

See also

关于超平面的更加详细的说明可以参考T. Hastie, R. Tibshirani 和 J. H. Friedman的书籍 Elements of Statistical Learning ， section 4.5 (Seperating Hyperplanes)。

最优超平面可以有无数种表达方式，即通过任意的缩放 $\beta$ 和 $\beta_{0}$ 。习惯上我们使用以下方式来表达最优超平面

$|\beta_{0} + \beta^{T} x| = 1$

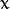式中 $x$ 表示离超平面最近的那些点。这些点被称为 支持向量**。该超平面也称为 **canonical 超平面.

通过几何学的知识，我们知道点 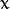$x$ 到超平面 $(\beta, \beta_{0})$ 的距离为:

$\mathrm{distance} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||}.$

特别的，对于 canonical 超平面, 表达式中的分子为1，因此支持向量到canonical 超平面的距离是

$\mathrm{distance}_{\text{ support vectors}} = \frac{|\beta_{0} + \beta^{T} x|}{||\beta||} = \frac{1}{||\beta||}.$

刚才我们介绍了间隔(margin),这里表示为 $M$ , 它的取值是最近距离的2倍:

$M = \frac{2}{||\beta||}$

最后最大化 $M$ 转化为在附加限制条件下最小化函数 $L(\beta)$ 。限制条件隐含超平面将所有训练样本 $x_{i}$ 正确分类的条件,

$\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \text{ subject to } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \text{ } \forall i,$

式中 $y_{i}$ 表示样本的类别标记。

这是一个拉格朗日优化问题，可以通过拉格朗日乘数法得到最优超平面的权重向量 $\beta$ 和偏置 $\beta_{0}$ 。

2 源码路径

支持向量机(SVM)介绍

\opencv\sources\samples\cpp\tutorial_code\ml\introduction_to_svm

测试所用操作系统： Windows 7 64bit
测试所用IDE版本：Visual Studio 2010

//--------------------------------------【程序说明】-------------------------------------------
//		程序描述：来自OpenCV安装目录下Samples文件夹中的官方示例程序-支持向量机SVM引导
//-------------------------------------------------------

//---------------------------------【头文件、命名空间包含部分】----------------------------
//		描述：包含程序所使用的头文件和命名空间
//-------------------------------------------------------------------------------------------------
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/ml/ml.hpp>
using namespace cv;


//-----------------------------------【main( )函数】--------------------------------------------
//		描述：控制台应用程序的入口函数，我们的程序从这里开始
//-------------------------------------------------------------------------------------------------
int main()
{
	// 视觉表达数据的设置（Data for visual representation）
	int width = 512, height = 512;
	Mat image = Mat::zeros(height, width, CV_8UC3);

	//建立训练数据（ Set up training data）
	//本例中的训练样本由分属于两个类别的2维点组成， 其中一类包含一个样本点，另一类包含三个点。
	//函数 CvSVM::train 要求训练数据储存于float类型的 Mat 结构中， 因此我们定义了以下矩阵:
	float labels[4] = {1.0, -1.0, -1.0, -1.0};
	Mat labelsMat(3, 1, CV_32FC1, labels);

	float trainingData[4][2] = { {501, 10}, {255, 10}, {501, 255}, {10, 501} };
	Mat trainingDataMat(3, 2, CV_32FC1, trainingData);


	//设置支持向量机的参数（Set up SVM's parameters）
	CvSVMParams params;
	params.svm_type    = CvSVM::C_SVC;
	params.kernel_type = CvSVM::LINEAR;
	params.term_crit   = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);

	// 训练支持向量机（Train the SVM）
	CvSVM SVM;
	SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params);

	Vec3b green(0,255,0), blue (255,0,0);
	//显示由SVM给出的决定区域 （Show the decision regions given by the SVM）
	for (int i = 0; i < image.rows; ++i)
		for (int j = 0; j < image.cols; ++j)
		{
			Mat sampleMat = (Mat_<float>(1,2) << i,j);
			float response = SVM.predict(sampleMat);

			if (response == 1)
				image.at<Vec3b>(j, i)  = green;
			else if (response == -1) 
				image.at<Vec3b>(j, i)  = blue;
		}

		//显示训练数据 （Show the training data）
		int thickness = -1;
		int lineType = 8;
		circle( image, Point(501,  10), 5, Scalar(  0,   0,   0), thickness, lineType);
		circle( image, Point(255,  10), 5, Scalar(255, 255, 255), thickness, lineType);
		circle( image, Point(501, 255), 5, Scalar(255, 255, 255), thickness, lineType);
		circle( image, Point( 10, 501), 5, Scalar(255, 255, 255), thickness, lineType);

		//显示支持向量 （Show support vectors）
		thickness = 2;
		lineType  = 8;
		int c     = SVM.get_support_vector_count();

		for (int i = 0; i < c; ++i)
		{
			const float* v = SVM.get_support_vector(i);
			circle( image,  Point( (int) v[0], (int) v[1]),   6,  Scalar(128, 128, 128), thickness, lineType);
		}

		imwrite("result.png", image);        // 保存图像

		imshow("SVM Simple Example", image); // 显示图像
		waitKey(0);

}

解释
1. 建立训练样本
本例中的训练样本由分属于两个类别的2维点组成，其中一类包含一个样本点，另一类包含三个点。
float labels[4] = {1.0, -1.0, -1.0, -1.0}; float trainingData[4][2] = {{501, 10}, {255, 10}, {501, 255}, {10, 501}};
函数 CvSVM::train 要求训练数据储存于float类型的 Mat 结构中，因此我们定义了以下矩阵:
Mat trainingDataMat(3, 2, CV_32FC1, trainingData); Mat labelsMat (3, 1, CV_32FC1, labels);
1. 设置SVM参数
  
  此教程中，我们以可线性分割的分属两类的训练样本简单讲解了SVM的基本原理。然而，SVM的实际应用情形可能复杂得多 (比如非线性分割数据问题，SVM核函数的选择问题等等)。总而言之，我们需要在训练之前对SVM做一些参数设定。这些参数保存在类 CvSVMParams 中。
  CvSVMParams params; params.svm_type = CvSVM::C_SVC; params.kernel_type = CvSVM::LINEAR; params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);
  - SVM类型. 这里我们选择了 CvSVM::C_SVC 类型，该类型可以用于n-类分类问题 (n $\geq$ 2)。这个参数定义在 CvSVMParams.svm_type 属性中.
    
    Note
    
    CvSVM::C_SVC 类型的重要特征是它可以处理非完美分类的问题 (及训练数据不可以完全的线性分割)。在本例中这一特征的意义并不大，因为我们的数据是可以线性分割的，我们这里选择它是因为它是最常被使用的SVM类型。
  - SVM 核类型. 我们没有讨论核函数，因为对于本例的样本，核函数的讨论没有必要。然而，有必要简单说一下核函数背后的主要思想，核函数的目的是为了将训练样本映射到更有利于可线性分割的样本集。映射的结果是增加了样本向量的维度，这一过程通过核函数完成。此处我们选择的核函数类型是 CvSVM::LINEAR 表示不需要进行映射。该参数由 CvSVMParams.kernel_type 属性定义。
  - 算法终止条件. SVM训练的过程就是一个通过迭代方式解决约束条件下的二次优化问题，这里我们指定一个最大迭代次数和容许误差，以允许算法在适当的条件下停止计算。该参数定义在 cvTermCriteria 结构中。
2. 训练支持向量机
  
  调用函数 CvSVM::train 来建立SVM模型。
  CvSVM SVM; SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params);
3. SVM区域分割
函数 CvSVM::predict 通过重建训练完毕的支持向量机来将输入的样本分类。本例中我们通过该函数给向量空间着色，及将图像中的每个像素当作卡迪尔平面上的一点，每一点的着色取决于SVM对该点的分类类别：绿色表示标记为1的点，蓝色表示标记为-1的点。
Vec3b green(0,255,0), blue (255,0,0); for (int i = 0; i < image.rows; ++i) for (int j = 0; j < image.cols; ++j) { Mat sampleMat = (Mat_<float>(1,2) << i,j); float response = SVM.predict(sampleMat); if (response == 1) image.at<Vec3b>(j, i) = green; else if (response == -1) image.at<Vec3b>(j, i) = blue; }
1. 支持向量
  
  这里用了几个函数来获取支持向量的信息。函数 CvSVM::get_support_vector_count 输出支持向量的数量，函数 CvSVM::get_support_vector 根据输入支持向量的索引来获取指定位置的支持向量。通过这一方法我们找到训练样本的支持向量并突出显示它们。
  int c = SVM.get_support_vector_count(); for (int i = 0; i < c; ++i) { const float* v = SVM.get_support_vector(i); // get and then highlight with grayscale circle( image, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thickness, lineType); }
结果
- 程序创建了一张图像，在其中显示了训练样本，其中一个类显示为白色圆圈，另一个类显示为黑色圆圈。
- 训练得到SVM，并将图像的每一个像素分类。分类的结果将图像分为蓝绿两部分，中间线就是最优分割超平面。
- 最后支持向量通过灰色边框加重显示。
。

支持向量机对线性不可分数据的处理

\opencv\sources\samples\cpp\tutorial_code\ml\non_linear_svms

支持向量机对线性不可分数据的处理

目标

本文档尝试解答如下问题:

在训练数据线性不可分时，如何定义此情形下支持向量机的最优化问题。
如何设置 CvSVMParams 中的参数来解决此类问题。

动机

为什么需要将支持向量机优化问题扩展到线性不可分的情形？在多数计算机视觉运用中，我们需要的不仅仅是一个简单的SVM线性分类器，我们需要更加强大的工具来解决 训练数据无法用一个超平面分割 的情形。

我们以人脸识别来做一个例子，训练数据包含一组人脸图像和一组非人脸图像(除了人脸之外的任何物体)。这些训练数据超级复杂，以至于为每个样本找到一个合适的表达 (特征向量) 以让它们能够线性分割是非常困难的。

最优化问题的扩展

还记得我们用支持向量机来找到一个最优超平面。既然现在训练数据线性不可分，我们必须承认这个最优超平面会将一些样本划分到错误的类别中。在这种情形下的优化问题，需要将 错分类(misclassification) 当作一个变量来考虑。新的模型需要包含原来线性可分情形下的最优化条件，即最大间隔(margin), 以及在线性不可分时分类错误最小化。

我们还是从最大化间隔这一条件来推导我们的最优化问题的模型(这在 前一节 已经讨论了):

$\min_{\beta, \beta_{0}} L(\beta) = \frac{1}{2}||\beta||^{2} \text{ subject to } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 \text{ } \forall i$

在这个模型中加入错分类变量有多种方法。比如，我们可以最小化一个函数，该函数定义为在原来模型的基础上再加上一个常量乘以样本被错误分类的次数:

$\min ||\beta||^{2} + C \text{(\# misclassication errors)}$

然而，这并不是一个好的解决方案，其中一个原因是它没有考虑错分类的样本距离同类样本所属区域的大小。因此一个更好的方法是考虑 错分类样本离同类区域的距离:

$\min ||\beta||^{2} + C \text{(distance of misclassified samples to their correct regions)}$

这里为每一个样本定义一个新的参数 $\xi_{i}$ ，这个参数包含对应样本离同类区域的距离。下图显示了两类线性不可分的样本，以及一个分割超平面和错分类样本距离同类区域的距离。

Samples misclassified and their distances to their correct regions

Note

图中只显示了错分类样本的距离，其余样本由于已经处于同类区域内部所以距离为零。

红色和蓝色直线表示各自区域的边际间隔，每个 $\xi_{i}$ 表示从错分类样本到同类区域边际间隔的距离。

最后我们得到最优问题的最终模型:

$\min_{\beta, \beta_{0}} L(\beta) = ||\beta||^{2} + C \sum_{i} {\xi_{i}} \text{ subject to } y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 - \xi_{i} \text{ and } \xi_{i} \geq 0 \text{ } \forall i$

关于参数C的选择，明显的取决于训练样本的分布情况。尽管并不存在一个普遍的答案，但是记住下面几点规则还是有用的:

C比较大时分类错误率较小，但是间隔也较小。在这种情形下，错分类对模型函数产生较大的影响，既然优化的目的是为了最小化这个模型函数，那么错分类的情形必然会受到抑制。
C比较小时间隔较大，但是分类错误率也较大。在这种情形下，模型函数中错分类之和这一项对优化过程的影响变小，优化过程将更加关注于寻找到一个能产生较大间隔的超平面。

//--------------------------------------【程序说明】-------------------------------------------
//		程序描述：来自OpenCV安装目录下Samples文件夹中的官方示例程序-支持向量机SVM之处理线性不可分数据
//---------------------------------------------------



//---------------------------------【头文件、命名空间包含部分】----------------------------
//		描述：包含程序所使用的头文件和命名空间
//------------------------------------------------------------------------------------------------
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/ml/ml.hpp>

#define NTRAINING_SAMPLES   100         // 每类训练样本的数量
#define FRAC_LINEAR_SEP     0.9f        //  部分(Fraction)线性可分的样本组成部分

using namespace cv;
using namespace std;


//-----------------------------------【main( )函数】--------------------------------------------
//		描述：控制台应用程序的入口函数，我们的程序从这里开始
//-------------------------------------------------------------------------------------------------
int main()
{
	//设置视觉表达的参数
	const int WIDTH = 512, HEIGHT = 512;
	Mat I = Mat::zeros(HEIGHT, WIDTH, CV_8UC3);

	//--------------------- 【1】随机建立训练数据 ---------------------------------------
	Mat trainData(2*NTRAINING_SAMPLES, 2, CV_32FC1);
	Mat labels   (2*NTRAINING_SAMPLES, 1, CV_32FC1);

	RNG rng(100); // 随机生成值

	//建立训练数据的线性可分的组成部分
	int nLinearSamples = (int) (FRAC_LINEAR_SEP * NTRAINING_SAMPLES);

	// 为Class1生成随机点
	Mat trainClass = trainData.rowRange(0, nLinearSamples);
	// 点的x坐标为[0,0.4)
	Mat c = trainClass.colRange(0, 1);
	rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(0.4 * WIDTH));
	// 点的Y坐标为[0,1)
	c = trainClass.colRange(1,2);
	rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

	// 为Class2生成随机点
	trainClass = trainData.rowRange(2*NTRAINING_SAMPLES-nLinearSamples, 2*NTRAINING_SAMPLES);
	// 点的x坐标为[0.6, 1]
	c = trainClass.colRange(0 , 1); 
	rng.fill(c, RNG::UNIFORM, Scalar(0.6*WIDTH), Scalar(WIDTH));
	// 点的Y坐标为[0, 1)
	c = trainClass.colRange(1,2);
	rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

	//------------------建立训练数据的非线性可分组成部分 ---------------

	// 随机生成Class1和Class2的点
	trainClass = trainData.rowRange(  nLinearSamples, 2*NTRAINING_SAMPLES-nLinearSamples);
	// 点的x坐标为[0.4, 0.6)
	c = trainClass.colRange(0,1);
	rng.fill(c, RNG::UNIFORM, Scalar(0.4*WIDTH), Scalar(0.6*WIDTH)); 
	// 点的y坐标为[0, 1)
	c = trainClass.colRange(1,2);
	rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

	//-------------------------设置类标签 ---------------------------------
	labels.rowRange(                0,   NTRAINING_SAMPLES).setTo(1);  // Class 1
	labels.rowRange(NTRAINING_SAMPLES, 2*NTRAINING_SAMPLES).setTo(2);  // Class 2

	//------------------------ 2. 设置支持向量机的参数 --------------------
	CvSVMParams params;
	params.svm_type    = SVM::C_SVC;
	params.C           = 0.1;
	params.kernel_type = SVM::LINEAR;
	params.term_crit   = TermCriteria(CV_TERMCRIT_ITER, (int)1e7, 1e-6);

	//------------------------ 3. 训练支持向量机 ----------------------------------------------------
	cout << "Starting training process" << endl;
	CvSVM svm;
	svm.train(trainData, labels, Mat(), Mat(), params);
	cout << "Finished training process" << endl;

	//------------------------ 4. 标出决策区域（decision regions） ----------------------------------------
	Vec3b green(0,100,0), blue (100,0,0);
	for (int i = 0; i < I.rows; ++i)
		for (int j = 0; j < I.cols; ++j)
		{
			Mat sampleMat = (Mat_<float>(1,2) << i, j);
			float response = svm.predict(sampleMat);

			if      (response == 1)    I.at<Vec3b>(j, i)  = green;
			else if (response == 2)    I.at<Vec3b>(j, i)  = blue;
		}

		//----------------------- 5. 显示训练数据（training data） --------------------------------------------
		int thick = -1;
		int lineType = 8;
		float px, py;
		// Class 1
		for (int i = 0; i < NTRAINING_SAMPLES; ++i)
		{
			px = trainData.at<float>(i,0);
			py = trainData.at<float>(i,1);
			circle(I, Point( (int) px,  (int) py ), 3, Scalar(0, 255, 0), thick, lineType);
		}
		// Class 2
		for (int i = NTRAINING_SAMPLES; i <2*NTRAINING_SAMPLES; ++i)
		{
			px = trainData.at<float>(i,0);
			py = trainData.at<float>(i,1);
			circle(I, Point( (int) px, (int) py ), 3, Scalar(255, 0, 0), thick, lineType);
		}

		//------------------------- 6. 显示支持向量（support vectors） --------------------------------------------
		thick = 2;
		lineType  = 8;
		int x     = svm.get_support_vector_count();

		for (int i = 0; i < x; ++i)
		{
			const float* v = svm.get_support_vector(i);
			circle( I,  Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thick, lineType);
		}

		imwrite("result.png", I);                      //保存图像到文件
		imshow("SVM for Non-Linear Training Data", I); // 显示最终窗口
		waitKey(0);
}

解释

建立训练样本

本例中的训练样本由分属于两个类别的2维点组成。为了让程序更加吸引人，我们用均匀概率密度函数(PDF)随机生成样本.

我们将样本的生成代码分成两部分。

在第一部分我们生成两类线性可分样本

 
    // class 1 随机样本生成
Mat trainClass = trainData.rowRange(0, nLinearSamples);
// x 坐标范围 [0, 0.4)
Mat c = trainClass.colRange(0, 1);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(0.4 * WIDTH));
// y 坐标范围 [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));

// class 2 随机样本生成
trainClass = trainData.rowRange(2*NTRAINING_SAMPLES-nLinearSamples, 2*NTRAINING_SAMPLES);
// x 坐标范围 [0.6, 1]
c = trainClass.colRange(0 , 1);
rng.fill(c, RNG::UNIFORM, Scalar(0.6*WIDTH), Scalar(WIDTH));
// y 坐标范围 [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));
 
   

在第二部分我们同时生成重叠分布线性不可分的两类样本.

 
    // classes 1 ， 2 随机样本生成
trainClass = trainData.rowRange(  nLinearSamples, 2*NTRAINING_SAMPLES-nLinearSamples);
// x 坐标范围  [0.4, 0.6)
c = trainClass.colRange(0,1);
rng.fill(c, RNG::UNIFORM, Scalar(0.4*WIDTH), Scalar(0.6*WIDTH));
// y 坐标范围  [0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(1), Scalar(HEIGHT));
 
   

设置SVM参数

See also

前一节 支持向量机(SVM)介绍 提到了类 CvSVMParams 中的一些参数需要在训练SVM之前设置。
CvSVMParams params;
params.svm_type    = SVM::C_SVC;
params.C              = 0.1;
params.kernel_type = SVM::LINEAR;
params.term_crit   = TermCriteria(CV_TERMCRIT_ITER, (int)1e7, 1e-6);
这里的设置和 前一节 的设置有两处不一样的地方

CvSVM::C_SVC. 此处取值较小，目的是优化时不过分惩罚分类错误。这样做的目的是为了得到一个与直觉预期比较接近的分隔线。您可以通过调整该参数来加深你对问题的理解。

Note

这里在两类之间重叠区域的点比较少，缩小 FRAC_LINEAR_SEP 会增加不可分区域的点数，此时 CvSVM::C_SVC 参数的调整对结果的影响深远。

算法终止条件. 最大迭代次数需要显著增加来容许非线性可分的训练数据，这里的最大迭代设置是前一节的10的5次方倍。

训练支持向量机

调用函数 CvSVM::train 来建立SVM模型。注意训练过程可能耗时比较长，您需要多一点耐心来等待。
CvSVM svm;
svm.train(trainData, labels, Mat(), Mat(), params);

SVM区域分割

函数 CvSVM::predict 通过重建训练完毕的支持向量机来将输入的样本分类。本例中我们通过该函数给向量空间着色，即将图像中的每个像素当作卡迪尔平面上的一点，每一点的着色取决于SVM对该点的分类类别：深绿色表示分类为1的点，深蓝色表示分类为2的点。
Vec3b green(0,100,0), blue (100,0,0);
for (int i = 0; i < I.rows; ++i)
     for (int j = 0; j < I.cols; ++j)
     {
          Mat sampleMat = (Mat_<float>(1,2) << i, j);
          float response = svm.predict(sampleMat);

          if      (response == 1)    I.at<Vec3b>(j, i)  = green;
          else if (response == 2)    I.at<Vec3b>(j, i)  = blue;
     }

显示训练样本

函数 circle 被用来显示训练样本。标记为1的样本用浅绿表示，标记为2的样本用浅蓝表示。

 
    int thick = -1;
int lineType = 8;
float px, py;
// Class 1
for (int i = 0; i < NTRAINING_SAMPLES; ++i)
{
     px = trainData.at<float>(i,0);
     py = trainData.at<float>(i,1);
     circle(I, Point( (int) px,  (int) py ), 3, Scalar(0, 255, 0), thick, lineType);
}
// Class 2
for (int i = NTRAINING_SAMPLES; i <2*NTRAINING_SAMPLES; ++i)
{
     px = trainData.at<float>(i,0);
     py = trainData.at<float>(i,1);
     circle(I, Point( (int) px, (int) py ), 3, Scalar(255, 0, 0), thick, lineType);
}
 
   

支持向量

这里用了几个函数来获取支持向量的信息。函数 CvSVM::get_support_vector_count 输出支持向量的数量，函数 CvSVM::get_support_vector 根据输入支持向量的索引来获取指定位置的支持向量。通过这一方法我们找到训练样本的支持向量并突出显示它们。
thick = 2;
lineType  = 8;
int x     = svm.get_support_vector_count();

for (int i = 0; i < x; ++i)
{
     const float* v = svm.get_support_vector(i);
     circle(     I,  Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thick, lineType);
}

结果

程序创建了一张图像，在其中显示了训练样本，其中一个类显示为浅绿色圆圈，另一个类显示为浅蓝色圆圈。
训练得到SVM，并将图像的每一个像素分类。分类的结果将图像分为蓝绿两部分，中间线就是最优分割超平面。由于样本非线性可分，自然就有一些被错分类的样本。一些绿色点被划分到蓝色区域，一些蓝色点被划分到绿色区域。
最后支持向量通过灰色边框加重显示。

Note

这里在两类之间重叠区域的点比较少，缩小 FRAC_LINEAR_SEP 会增加不可分区域的点数，此时 CvSVM::C_SVC 参数的调整对结果的影响深远。

#define FRAC_LINEAR_SEP 0.4f // 部分(Fraction)线性可分的样本组成部分

CvSVMParams params;
params.svm_type = SVM::C_SVC;
params.C = 1;
params.kernel_type = SVM::LINEAR;
params.term_crit = TermCriteria(CV_TERMCRIT_ITER, (int)1e7, 1e-6);

params.kernel_type = CvSVM::RBF;

params.kernel_type =CvSVM::SIGMOID ;

params.C = 0.01;

params.term_crit = TermCriteria(CV_TERMCRIT_ITER, (int)1e2, 1e-3);

Opencv中的SVM参数优化

参考 http://www.itnose.net/detail/6095711.html

SVM（支持向量机）是机器学习算法里用得最多的算法。SVM最常用的是用于分类，不过SVM也可以用于回归，我的实验中就是用SVM来实现SVR（支持向量回归）。对于功能这么强的算法，opencv中自然也是有集成好了，我们可以直接调用。

网上讲opencv中SVM使用的文章有很多，但讲SVM参数优化的文章却很少。所以在这里不重点讲怎么使用SVM，而是谈谈怎样通过opencv中自带的库优化SVM中的各参数。

相信用SVM做过实验的人都知道，SVM的各参数对实验结果有很大的影响，比如C，gama，P，coef等等。下面就是CvSVMParams类的原型。

C++: CvSVMParams::CvSVMParams()

C++: CvSVMParams::CvSVMParams(int svm_type,

int kernel_type,

double degree,

double gamma,

double coef0,

double Cvalue,

double nu,

double p,

CvMat* class_weights,

CvTermCriteria term_crit

　　　　　　　　)

构造函数的参数(一共10个)：

<1> svm_type:指定SVM的类型(5种)：

CvSVM::C_SVC : C类支持向量分类机。 n类分组 (n≥2)，允许用异常值惩罚因子C进行不完全分类。
CvSVM::NU_SVC : 类支持向量分类机。n类似然不完全分类的分类器。参数为取代C（其值在区间【0，1】中，nu越大，决策边界越平滑）。
CvSVM::ONE_CLASS : 单分类器，所有的训练数据提取自同一个类里，然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
CvSVM::EPS_SVR : 类支持向量回归机。训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
CvSVM::NU_SVR : 类支持向量回归机。代替了 p。

<2>kernel_type:SVM的内核类型(4种)：

CvSVM::LINEAR : 线性内核，没有任何向映射至高维空间，线性区分（或回归）在原始特征空间中被完成，这是最快的选择。

CvSVM::POLY : 多项式内核：

CvSVM::RBF : 基于径向的函数，对于大多数情况都是一个较好的选择：

CvSVM::SIGMOID : Sigmoid函数内核：

<3> degree:内核函数（POLY）的参数degree。

<4> gamma:内核函数（POLY/ RBF/ SIGMOID）的参数 opencv,svm,优化,参数4

。

<5> coef0:内核函数（POLY/ SIGMOID）的参数coef0。

<6> Cvalue:SVM类型（C_SVC/ EPS_SVR/ NU_SVR）的参数C。

<7> nu:SVM类型（NU_SVC/ ONE_CLASS/ NU_SVR）的参数。

<8> p:SVM类型（EPS_SVR）的参数 opencv,svm,优化,参数6

。

<9> class_weights:C_SVC中的可选权重，赋给指定的类，乘以C以后变成 opencv,svm,优化,参数7

。所以这些权重影响不同类别的错误分类惩罚项。权重越大，某一类别的误分类数据的惩罚项就越大。

<10> term_crit:SVM的迭代训练过程的中止条件，解决部分受约束二次最优问题。您可以指定的公差和/或最大迭代次数。

当然对于一个特定的SVM训练器，里面的所有参数不一定全用。比如我用的svm_type为EPS_SVR，那么我要用到的参数主要就是p,c,gama这三个参数。下面是设置参数的代码

	CvSVMParams param;  
	param.svm_type = CvSVM::EPS_SVR;  //我的实验是用SVR作回归分析，可能大部分人的实验是用SVM来分类，方法都一样
	param.kernel_type = CvSVM::RBF;  
	param.C = 1;  
	param.p = 5e-3;  
	param.gamma = 0.01;  
	param.term_crit = cvTermCriteria(CV_TERMCRIT_EPS, 100, 5e-3);

设置参数后就可以用CvSVM.train()进行训练了，下面是train的原型

C++: bool CvSVM::train(const Mat& trainData,
　　　　　　const Mat& responses,
const Mat& varIdx=Mat(),
const Mat& sampleIdx=Mat(),
CvSVMParams params=CvSVMParams()
)

我在用train完成训练预测时出现了过拟合的情况，即对于训练集的数据有很好的预测结果，但对不在训练集的测试集预测值都一样。于是我开始调整参数，调了半天也没个好结果。

后面我发现其实opencv中SVM类是提供了优化参数值功能的，瞬间感觉世界美好了。下面讲讲具体的做法。

要让svm自动优化参数，那么训练时就不能再用train函数了，而应该用train_auto函数。下面是train_auto的函数原型

C++: bool CvSVM::train_auto(const Mat& trainData,

　　　　　　　　const Mat& responses,

const Mat& varIdx,

const Mat& sampleIdx,

CvSVMParams params,

int k_fold=10,

CvParamGrid Cgrid=CvSVM::get_default_grid(CvSVM::C),

CvParamGrid gammaGrid=CvSVM::get_default_grid(CvSVM::GAMMA),

CvParamGrid pGrid=CvSVM::get_default_grid(CvSVM::P),

CvParamGrid nuGrid=CvSVM::get_default_grid(CvSVM::NU),

CvParamGrid coeffGrid=CvSVM::get_default_grid(CvSVM::COEF),

CvParamGrid degreeGrid=CvSVM::get_default_grid(CvSVM::DEGREE),

bool balanced=false

)

自动训练函数的参数注释(13个)

前5个参数参考构造函数的参数注释。
k_fold: 交叉验证参数。训练集被分成k_fold的自子集。其中一个子集是用来测试模型，其他子集则成为训练集。所以，SVM算法复杂度是执行k_fold的次数。
*Grid: (6个)对应的SVM迭代网格参数。
balanced: 如果是true则这是一个2类分类问题。这将会创建更多的平衡交叉验证子集。
自动训练函数的使用说明

这个方法根据CvSVMParams中的最佳参数C, gamma, p, nu, coef0, degree自动训练SVM模型。
参数被认为是最佳的交叉验证，其测试集预估错误最小。
如果没有需要优化的参数，相应的网格步骤应该被设置为小于或等于1的值。例如，为了避免gamma的优化，设置gamma_grid.step = 0，gamma_grid.min_val， gamma_grid.max_val 为任意数值。所以params.gamma 由gamma得出。
最后，如果参数优化是必需的，但是相应的网格却不确定，你可能需要调用函数CvSVM::get_default_grid()，创建一个网格。例如，对于gamma，调用CvSVM::get_default_grid(CvSVM::GAMMA)。

该函数为分类运行 (params.svm_type=CvSVM::C_SVC 或者 params.svm_type=CvSVM::NU_SVC) 和为回归运行 (params.svm_type=CvSVM::EPS_SVR 或者 params.svm_type=CvSVM::NU_SVR)效果一样好。如果params.svm_type=CvSVM::ONE_CLASS，没有优化，并指定执行一般的SVM。

这里需要注意的是，对于需要的优化的参数虽然train_auto可以自动选择最优值，但在代码中也要先赋初始值，要不然编译能通过，但运行时会报错。下面是示例代码

	CvSVMParams param;  
	param.svm_type = CvSVM::EPS_SVR;  
	param.kernel_type = CvSVM::RBF;  
	param.C = 1;  //给参数赋初始值
	param.p = 5e-3;  //给参数赋初始值
	param.gamma = 0.01;  //给参数赋初始值
	param.term_crit = cvTermCriteria(CV_TERMCRIT_EPS, 100, 5e-3); 
	//对不用的参数step设为0
	CvParamGrid nuGrid = CvParamGrid(1,1,0.0);
	CvParamGrid coeffGrid = CvParamGrid(1,1,0.0);
	CvParamGrid degreeGrid = CvParamGrid(1,1,0.0);

	CvSVM regressor;
	regressor.train_auto(PCA_training,tr_label,NULL,NULL,param,
		10,
		regressor.get_default_grid(CvSVM::C),
		regressor.get_default_grid(CvSVM::GAMMA),
		regressor.get_default_grid(CvSVM::P),
		nuGrid,
		coeffGrid,
		degreeGrid);

用上面的代码的就可以自动训练优化出参数了，最后想查看优化后的参数值可以使用CvSVMParams params_re = regressor.get_params()函数来获得各优化后的参数值。

CvSVMParams params_re = regressor.get_params();
	regressor.save("training_srv.xml");
	float C = params_re.C;
	float P = params_re.p;
	float gamma = params_re.gamma;
	printf("\nParms: C = %f, P = %f,gamma = %f \n",C,P,gamma);

参考http://blog.csdn.net/yang_xian521/article/details/6969904

1）设置训练样本集

需要两组数据，一组是数据的类别，一组是数据的向量信息。

2）设置SVM参数

利用CvSVMParams类实现类内的成员变量svm_type表示SVM类型：

CvSVM：：C_SVC C-SVC

CvSVM：：NU_SVC v-SVC

CvSVM：：ONE_CLASS 一类SVM

CvSVM：：EPS_SVR e-SVR

CvSVM：：NU_SVR v-SVR

成员变量kernel_type表示核函数的类型：

CvSVM：：LINEAR 线性：u‘v

CvSVM：：POLY 多项式：(r*u'v + coef0)^degree

CvSVM：：RBF RBF函数：exp(-r|u-v|^2)

CvSVM：：SIGMOID sigmoid函数：tanh(r*u'v + coef0)

成员变量degree针对多项式核函数degree的设置，gamma针对多项式/rbf/sigmoid核函数的设置，coef0针对多项式/sigmoid核函数的设置，Cvalue为损失函数，在C-SVC、e-SVR、v-SVR中有效，nu设置v-SVC、一类SVM和v-SVR参数，p为设置e-SVR中损失函数的值，class_weightsC_SVC的权重，term_crit为SVM训练过程的终止条件。其中默认值degree = 0，gamma = 1，coef0 = 0，Cvalue = 1，nu = 0，p = 0，class_weights = 0