StarNet（2024 CVPR）

论文标题	Rewrite the Stars
论文作者	Xu Ma, Xiyang Dai, Yue Bai, Yizhou Wang, Yun Fu
发表日期	2024年03月01日
GB引用	> Ma Xu, Dai Xiyang, Bai Yue, et al. Rewrite the Stars[J]. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2024: 5694-5703.
DOI	10.1109/CVPR52733.2024.00544

论文地址：https://arxiv.org/pdf/2403.19967

摘要

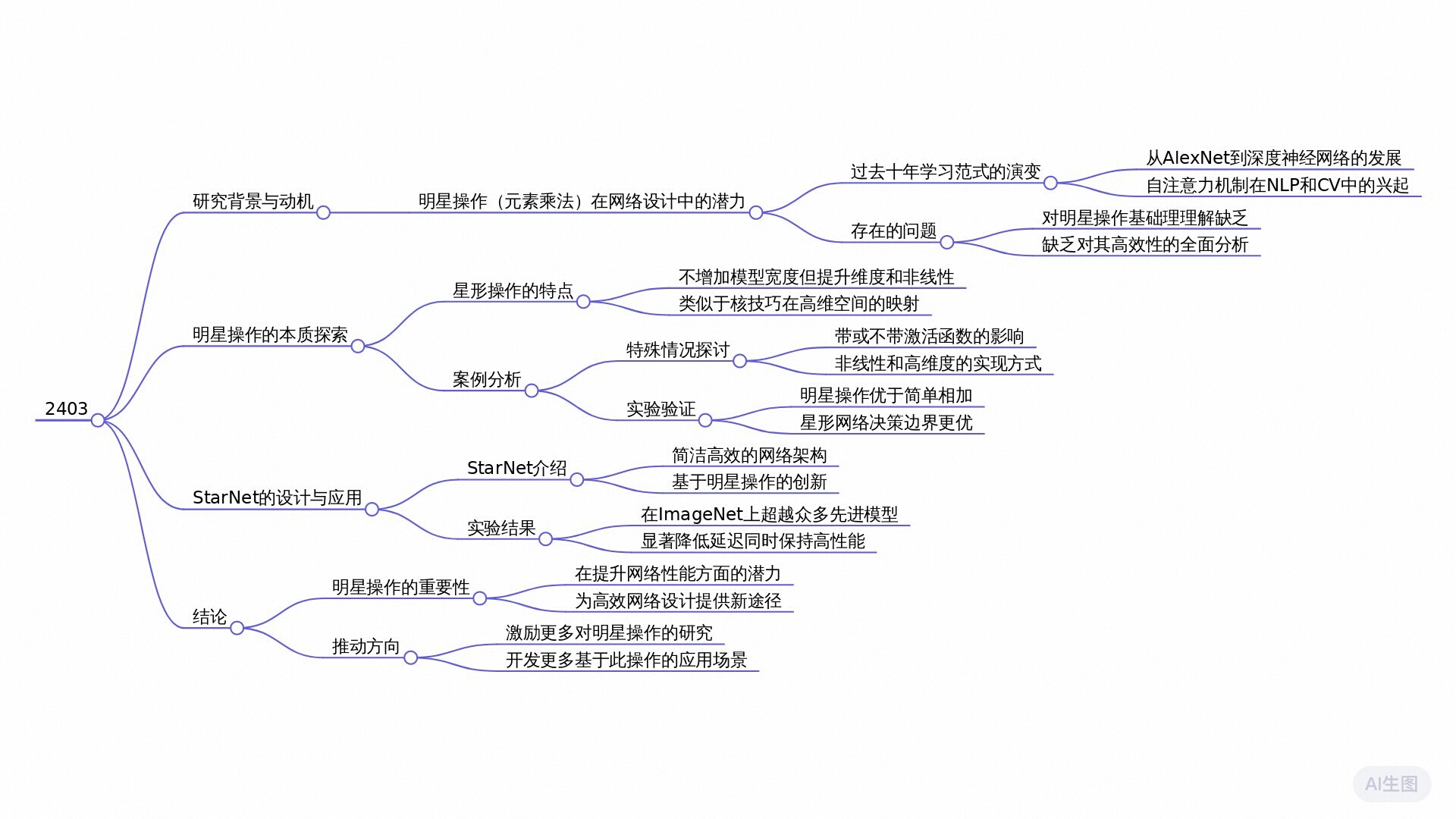
本研究探讨了“星操作”在神经网络设计中的应用，该操作通过逐元素相乘将输入映射到高维非线性特征空间。研究发现，这种操作在保持紧凑结构的同时，能显著提升模型性能和降低延迟。研究引入了StarNet模型，展示了其在不同任务中优于其他高效模型的表现。实验结果表明，星操作不仅提升了模型的准确性，还增强了其在低延迟设备上的表现。

全文摘要

该论文题为《Rewrite the Stars》，主要研究了在网络设计中“星操作”（元素逐个相乘）的潜力。尽管该操作的直观性得到广泛认可，但其理论基础仍然未被深入探讨。研究表明，星操作能够将输入映射到高维、非线性的特征空间，这一特性与核函数的原理相似，但无需扩大网络宽度。

论文提出了一种名为StarNet的高效模型原型，该模型在保持较小结构和低延迟的同时，展现出卓越的性能。研究结果显示，相较于传统的求和操作，星操作在不同宽度和深度的网络中，均能显著提高模型的准确性。这表明星操作在设计高效神经网络中具有优越性，特别适合用于资源受限的应用场景。

论文的独特之处在于其系统性地揭示了星操作所带来的显著优势，并通过理论和实证分析证明了其在隐式高维特征空间中的有效性。论文呼吁进一步探索星操作在不同任务中的应用潜力，提供了可用的代码以便研究者进行试验。

研究问题

为什么星操作（元素乘法）能够比传统的加法操作更有效地提高网络性能，并且能够在低维度空间中实现高维度特征的映射？

研究方法

实验研究： 通过构建名为DemoNet的网络，并在其中应用星操作或求和操作来融合特征，从而验证星操作的有效性和优越性。实验结果显示，无论网络深度和宽度如何变化，星操作始终优于求和操作。

定量研究： 通过对不同宽度和深度下的DemoNet进行实验，系统地收集和分析数据，展示了星操作在提高网络性能方面的显著优势。具体表现为表2和表3中星操作相对于求和操作的准确性提升。

混合方法研究： 结合定性分析和定量数据，从多个角度探讨星操作的特性和优势。例如，通过决策边界比较和激活函数去除实验，进一步证实了星操作的有效性。

现象学研究： 深入分析星操作在隐式高维空间中的表现，揭示其背后的数学原理和非线性特性。通过将星操作与多项式核函数进行类比，展示了其生成高维非线性特征空间的能力。

模拟研究： 通过构建StarNet网络原型，模拟星操作在实际应用中的表现，验证其在高效网络设计中的潜力。StarNet在多种硬件平台上的实验结果表明，星操作不仅提高了网络性能，还降低了计算复杂度。

研究思路

这篇论文的研究思路是围绕“星操作”（element-wise multiplication）在网络设计中的潜在能力展开的。研究者们尝试揭示星操作如何能够将输入映射到高维非线性特征空间，这一特性类似于核技巧，但不需要扩展网络宽度。研究的核心内容及其主要框架、方法、技术路线和创新点如下：

研究的理论基础是星操作的能力，具体表现为其能够在相对低维的空间内，通过元素级乘法（星操作）实现高维特征的表示。论文指出，星操作的工作方式可以被视为多项式核函数的一种实现方式。这使得研究者们能在不增加计算资源的情况下，通过堆叠多个层级，逐渐生成接近无限维度的特征。这一理论框架为后续网络模型（StarNet）的构建提供了基础。

具体方法和技术路线：

星操作分析：对星操作的数学性质进行详细分析，指出其能够在一层中生成约 $(d\sqrt{2}{)}^2$ 线性无关的特征表示。这是通过分析星操作的形式（ $\left(\begin{array}{c}{\mathrm{W}}_1^{\mathrm{T}}\mathrm{X}+{\mathrm{B}}_1\end{array}\right)\star \left(\begin{array}{c}{\mathrm{W}}_2^{\mathrm{T}}\mathrm{X}+{\mathrm{B}}_2\end{array}\right)$）实现的。

多层堆叠的能力：研究者们通过递归方式推导出，随着网络层数的增加，隐式特征空间将以指数方式增长，得出每一层的输出特征空间维度的表达式。

模型构建：在理论分析的基础上，研究者们提出了StarNet作为一个实证模型。StarNet的设计非常简单并直观，专注于在有效预算和紧凑结构下实现高效性能。

实验验证：通过一系列实验，验证星操作相较于传统的求和操作在性能上的优势，并测试StarNet在多个基准数据集上的表现。

重写 Stars 操作

我们从重写星号操作开始，以明确展示它实现 极高维度 的能力。然后我们证明在多层之后，星号可以显著增加隐式维度到接近无穷大。随后进行了讨论。

一层中的 Star 操作

在单层神经网络中，星号操作通常写为 $\left(\begin{array}{c}{\mathrm{W}}_1^{\mathrm{T}}\mathrm{X}+{\mathrm{B}}_1\end{array}\right)\ast \left(\begin{array}{c}{\mathrm{W}}_2^{\mathrm{T}}\mathrm{X}+{\mathrm{B}}_2\end{array}\right)$，表示通过逐元素乘法融合两个线性变换特征。为了方便，我们将权重矩阵和偏差合并为一个实体，记作 $\mathrm{W}=\left[\begin{array}{c}\mathrm{W}\\ \mathrm{B}\end{array}\right]$ ，类似地， $\mathrm{X}=\left[\begin{array}{c}\mathrm{X}\\ 1\end{array}\right]$ ，结果为星操作 $\left({\mathrm{W}}_1^{\mathrm{T}}\mathrm{X}\right)\ast \left({\mathrm{W}}_2^{\mathrm{T}}\mathrm{X}\right)$ 。为了简化分析，我们关注只涉及一个输出通道变换和单个输入元素的情况。具体来说，我们定义 $w_1,w_2,x\in {\mathbb{R}}^{(d+1)\times 1}$，其中 $d$ 是输入通道数。它可以很容易地扩展到多个输出通道 ${\mathrm{W}}_1,{\mathrm{W}}_2\in {\mathbb{R}}^{(d+1)\times \left(d^{\prime }+1\right)}$ 和处理多个特征元素，其中 $\mathrm{X}\in {\mathbb{R}}^{(d+1)\times n}$。

通常，我们可以重写星号操作为：

$w_1^{\mathrm{T}}x\ast w_2^{\mathrm{T}}x(1)$

= ( ∑ i = 1 d + 1 w 1 i x i ) ∗ ( ∑ j = 1 d + 1