【智能算法】布谷鸟搜索算法（CS)原理及实现

---

1.背景

2009年，Yang等人受到布谷鸟繁衍自然行为影响，提出了布谷鸟搜索算法(Cuckoo Search，CS)。

2.算法原理

2.1算法思想

布谷鸟繁衍特点寄生，将卵产在其他鸟类的巢穴中。一般情况下，布谷鸟蛋的孵化速度比寄主蛋快。一旦第一只布谷鸟雏鸟孵化，它会迅速推出其他蛋，增加寄主对它的食物供给。研究还指出，杜鹃雏鸟可以模仿寄主雏鸟的叫声，以获取更多被喂食的机会。（适应度越高，蛋获得能量越高）
三条理想化假设：

• 布谷鸟每次产下一枚蛋，随机进入寄主巢穴
• 具有最优质蛋的巢穴将会被保留（适应度最高）
• 寄主巢穴固定，有一定概率$Pa$发现布谷鸟蛋，寄主可以消灭该蛋或放弃旧巢另建新巢

2.2算法过程

群体位置初始化:
$$x=lb+rand\ast (ub-lb)$$
其中，$ub,lb$分别代表布谷鸟上下位置边界。
局部探索：
$$x_i^{t+1}=x_i^t+\alpha s\otimes H(p_a-ϵ)\otimes (x_j^t-x_k^t)$$
全局探索：
$$x_i^{t+1}=x_i^t+\alpha L(s,\lambda )$$
其中，$L(s,\lambda )$表示Lévy飞行：
$$L(s,\lambda )=\frac{\lambda \Gamma (\lambda )\sin (\pi \lambda /2)}{\pi }\frac{1}{s^{1+\lambda }},(s\gg s_0>0)$$
Lévy 飞行生成随机数应包括两个步骤：随机方向的选择和服从 Lévy 分布的步长的生成。方向服从均匀分布，步长由Mantegna算法给出：
$$s=\frac{U}{|V{|}^{1/\lambda }}$$
其中，$U\sim N(0,{\sigma }^2),V\sim N(0,1)$。方差表述为：
$${\sigma }^2=[\frac{\Gamma (1+\lambda )}{\lambda \Gamma ((1+\lambda )/2)}\cdot \frac{\sin (\pi \lambda /2)}{2^{(\lambda -1)/2}}{]}^{1/\lambda }$$
伪代码

3.代码实现

% 布谷鸟算法                   
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = CS(pop, maxIter,lb,ub,dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 控制参数
pa=0.25; 
%% 初始化种群
nest = zeros(pop, dim);
for i = 1:dim
    nest(:,i) = lb(i) + (ub(i) - lb(i)) * rand(pop, 1);
end
%% 计算适应度
fitness = zeros(1, pop);
for i = 1:pop
    fitness(i) = fobj(nest(i,:));
end
%% 记录
[SortFitness, SortIdx] = sort(fitness);
Best_fitness = SortFitness(1);
Best_pos = nest(SortIdx(1),:);
%% 迭代
for iter=1:maxIter
    % Levy飞行获得新解
     new_nest=get_cuckoos(nest,Best_pos,lb,ub);   
     [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness, fobj);
    % Pa概率遗弃
      new_nest=empty_nests(nest,lb,ub,pa) ;
    
      [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness, fobj);
 
    if fnew<Best_fitness
        Best_fitness=fnew;
        Best_pos=best;
    end
    
    Iter_curve(iter) = Best_fitness;
    History_best{iter} = Best_pos;
    History_pos{iter} = new_nest;
end 
end
%% Levy飞行
function nest=get_cuckoos(nest,best,Lb,Ub)
n=size(nest,1);
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);

for j=1:n
    s=nest(j,:);
    % Levy飞行步长求解
    u=randn(size(s))*sigma;
    v=randn(size(s));
    step=u./abs(v).^(1/beta);
     
    stepsize=0.01*step.*(s-best);
    s=s+stepsize.*randn(size(s));
    % 边界限制
   nest(j,:)=simplebounds(s,Lb,Ub);
end
end
%%
function [fmin,best,nest,fitness]=get_best_nest(nest,newnest,fitness,fobj)
for j=1:size(nest,1)
    fnew=fobj(newnest(j,:));
    if fnew<=fitness(j)
       fitness(j)=fnew;
       nest(j,:)=newnest(j,:);
    end
end
[fmin,K]=min(fitness) ;
best=nest(K,:);
end
%% 替换巢
function new_nest=empty_nests(nest,Lb,Ub,pa)
n=size(nest,1);
K=rand(size(nest))>pa;

%% 通过偏置/选择性随机游走的新解决方案
stepsize=rand*(nest(randperm(n),:)-nest(randperm(n),:));
new_nest=nest+stepsize.*K;
for j=1:size(new_nest,1)
    s=new_nest(j,:);
  new_nest(j,:)=simplebounds(s,Lb,Ub);  
end
end
% 边界限制
function s=simplebounds(s,Lb,Ub)
  ns_tmp=s;
  I=ns_tmp<Lb;
  ns_tmp(I)=Lb(I);
  
  J=ns_tmp>Ub;
  ns_tmp(J)=Ub(J);
  s=ns_tmp;
end

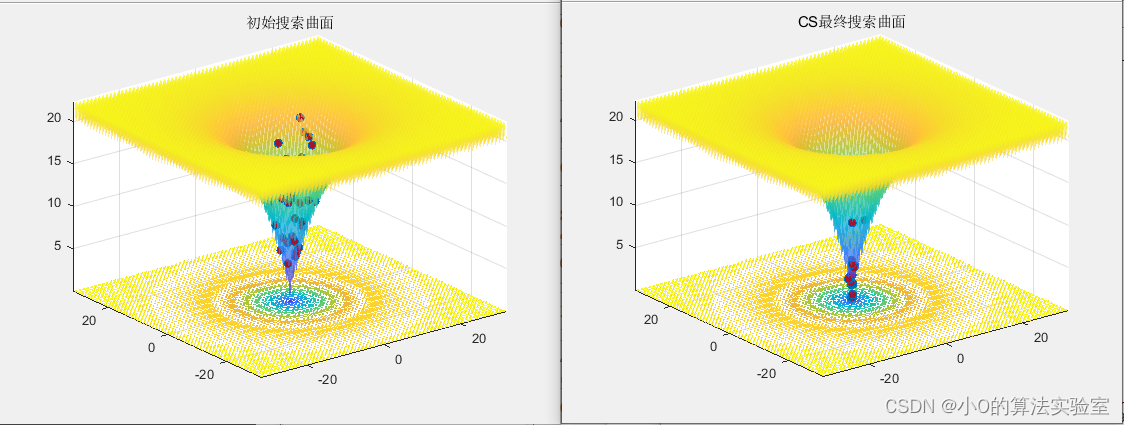
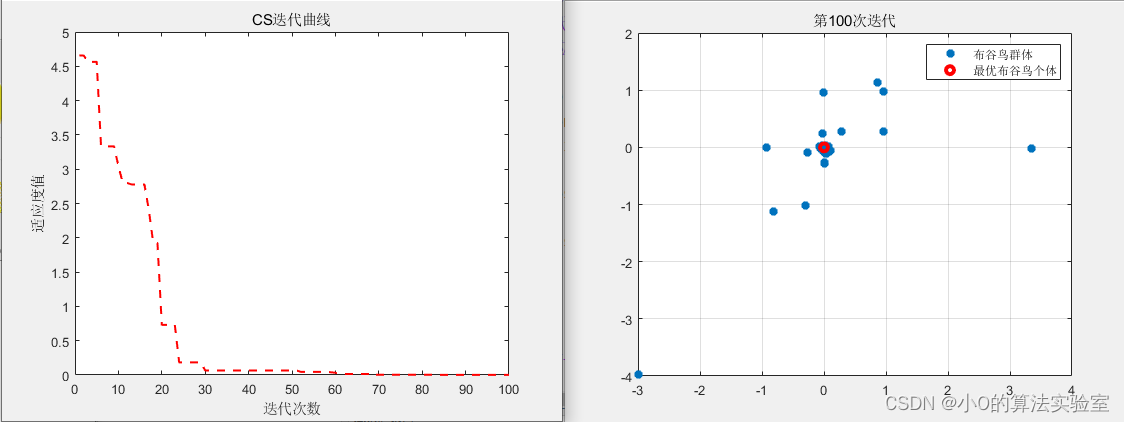
优化问题
以CEC2005测试函数为例

4.参考文献

【1】Yang X S, Deb S. Cuckoo search via Lévy flights[C]//2009 World congress on nature & biologically inspired computing (NaBIC). Ieee, 2009: 210-214.
【2】Mantegna RN. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic process. Phys Rev E 1994;49(5):4677–83.