【智能算法】麻雀搜索算法（SSA）原理及实现

小O的算法实验室

已于 2024-03-10 22:32:58 修改

阅读量1.3w

点赞数 53

分类专栏：智能算法文章标签：算法

于 2024-03-06 23:09:46 首次发布

本文链接：https://blog.csdn.net/Logic_9527/article/details/136519209

版权

智能算法专栏收录该内容

476 篇文章

订阅专栏

在这里插入图片描述

1.背景

2020年，Xue等人受麻雀觅食行为和逃避觅食者自然行为启发，提出了麻雀搜索算法(Sparrow Search Algorithm, SSA)。

2.算法原理

2.1算法思想

自然界中麻雀主要有觅食和反觅食两种行为：

觅食：麻雀中分为探索者和追随者，能够寻找较好食物的麻雀（适应度函数较高）为探索者，其余麻雀为追随者受到探索者方向影响
反觅食：麻雀群体中一定比例的麻雀会进行侦察，当发现觅食者来临时会做出相应的行为

2.2算法过程

群体位置初始化:
$X = l b + r an d * (u b - l b)$
其中， $u b, l b$ 分别代表种群上下位置边界。
探索者位置更新：
$x_{i}^{t+1}=\begin{cases}x_{i}^{t}*\exp{(\frac{-i}{\alpha *iter_{\max}})},R_{2}<ST\\x_{i}^{t}+Q,R_{2}\geq ST\end{cases}$
其中， $R_2,ST$ 分别为安全值和预警值。当 $R_2<ST$ 时，麻雀进行全局搜索觅食；当 $R_2\geq ST$ 时，麻雀以正态分布进行随机游走。
追随者位置更新：
$x_{i}^{t+1}=\begin{cases}Q\cdot\exp\left(\frac{x_{\text{worst}}^t-x_{i}^t}{i^2}\right),i>n/2\\x_{p}^{t+1}+|x_{i}^t-x_{p}^{t+1}|*A^+,\text{otherwise}\end{cases}$
当 $i > n /2$ 时，适应度较低的麻雀没有获取到食物，因此需要获得更多食物；其他情况说明，麻雀在当前最优位置附近随机寻找一个位置。
侦察预警：
$x_{i}^{t+1}=\begin{cases}xb_{i}^{t}+\beta *(x_{i}^{t}-xb_{i}^{t}),f_{i}\neq f_{g}\\ x_{i}^{t}+K\Bigg(\frac{x_{i}^t-xw_{i}^t}{\mid f_i-f_w\mid+\varepsilon}\Bigg),f_{i}=f_{g}\end{cases}$
当 $f_i \neq f_g$ ，麻雀正处于种群的边缘，容易受到觅食者攻击，此时朝着最优麻雀飞行；当 $f_i=f_g$ 时，此时麻雀处于危险位置，远离最差麻雀位置。
伪代码
在这里插入图片描述

3.代码实现

% 麻雀优化算法
function [Best_pos,Best_fitness ,Iter_curve,History_pos, History_best] = SSA(pop, M,c,d,dim,fobj )
%input
%pop 种群数量
%dim 问题维数
%c 变量上边界最大值
%d 变量下边界最小值
%fobj 适应度函数
%M 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优麻雀位置
%% 参数
P_percent = 0.2; %探索者比例
pNum = round(pop *  P_percent);
lb= c.*ones( 1,dim );    %约束上限
ub= d.*ones( 1,dim );    %约束下限
%% 位置初始化
for i = 1 : pop    
    x(i, :) = lb + (ub - lb) .* rand( 1, dim );  
    fit(i) = fobj(x(i, :)) ;              
end
% 以下找到最小值对应的麻雀群
pFit = fit;                      
pX = x;    
[ Best_fitness, bestI ] = min( fit ); 
Best_pos = x( bestI, : );            
%% 迭代
for t = 1 : M      
  [ ans, sortIndex ] = sort(pFit);
     
  [fmax,B]=max( pFit );
   worse= x(B,:);         %找到最差的个体      

   r2=rand(1);
 if(r2<0.8)
    for i = 1 : pNum                                                        % Equation (3)
         r1=rand(1);
        x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M)); %将种群按适应度排序后更新 
        x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );  %将种群限制在约束范围内
        fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );   
    end
  else
  for i = 1 : pNum            
  x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
  x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
  fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );       
  end      
end
 [ fMMin, bestII ] = min( fit );      
  bestXX = x( bestII, : );            
  
   for i = ( pNum + 1 ) : pop                     % Equation (4)
         A=floor(rand(1,dim)*2)*2-1;           %产生1和-1的随机数
         
          if( i>(pop/2))
           x( sortIndex(i ), : )=randn(1)*exp((worse-pX( sortIndex( i ), : ))/(i)^2);  
          else
        x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);  

         end  
        x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );  %更新后种群的限制在变量范围
        fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );                    %更新过后重新计算适应度
   end
  c=randperm(numel(sortIndex));
   b=sortIndex(c(1:20));
  for j =  1  : length(b)      % Equation (5)
    if( pFit( sortIndex( b(j) ) )>(Best_fitness) )
         %如果适应度比最开始最小适应度差的话，就在原来的最好种群上增长一部分值
        x( sortIndex( b(j) ), : )=Best_pos+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -Best_pos)));
        
        else
        %如果适应度达到开始最小的适应度值，就在原来的最好种群上随机增长或减小一部分
        x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);

          end
        x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
       
       fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );
 end
    for i = 1 : pop 
        if ( fit( i ) < pFit( i ) )
            pFit( i ) = fit( i );
            pX( i, : ) = x( i, : );
        end
        
        if( pFit( i ) < Best_fitness )  
           Best_fitness= pFit( i );
            Best_pos = pX( i, : );

        end
    end
  
    Iter_curve(t)=Best_fitness;
    History_pos{t} = x;
    History_best{t} =  Best_pos;
end

function s = Bounds( s, Lb, Ub)
  % Apply the lower bound vector
  temp = s;
  I = temp < Lb;
  temp(I) = Lb(I);
  
  % Apply the upper bound vector 
  J = temp > Ub;
  temp(J) = Ub(J);
  % Update this new move 
  s = temp;

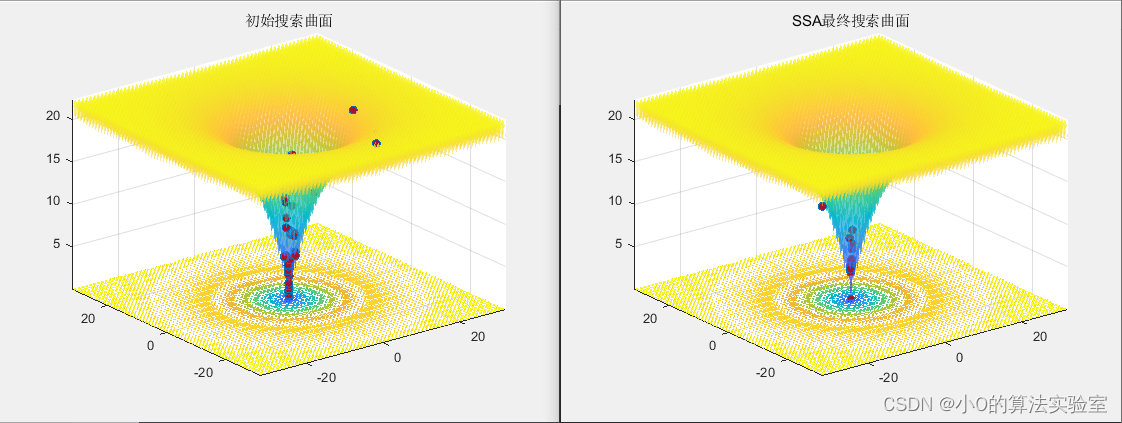
优化问题
以CEC2005测试函数为例

clear,clc,close all
x = -32:0.1:32;
y = x;
L = length(x);
for i = 1:L
    for j = 1:L
        f(i,j) = fun([x(i) y(j)]);
    end
end
surfc(x, y, f, 'LineStyle', 'none', 'FaceAlpha',0.5);

% 设定麻雀参数
pop = 50;
dim = 2;
ub = 32;
lb = -32;
maxIter = 100;
fobj = @(x) fun(x);

% 求解
[Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = SSA(pop, maxIter, lb, ub, dim,fobj);

在这里插入图片描述

4.参考文献

[1] Xue J, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems science & control engineering, 2020, 8(1): 22-34.