发论文创新点来了！KAN+时间序列预测，更高性能表现、更低资源占用

最新推荐文章于 2024-11-01 14:43:59 发布

马拉AI

最新推荐文章于 2024-11-01 14:43:59 发布

阅读量1.2k

点赞数 23

文章标签： KAN 时间序列

本文链接：https://blog.csdn.net/Mikasa33/article/details/142848640

版权

还记得因其独特的设计而迅速走红的KAN模型吗！这一模型的核心创新在于将激活函数直接应用于权重，并将其参数化为样条曲线，从而赋予了模型强大的函数拟合能力以及更好的可解释性。这些特性使得KAN在处理时间序列数据中的复杂关系和非线性模式时表现出色，为时间序列分析和预测提供了新的视角。

尽管KAN模型在单独使用时可能会遇到训练速度较慢的问题，但通过与其他模型（如LSTM、注意力机制等）结合，并采用优化策略，可以显著提升其性能。为了帮助大家快速掌握这一创新方向，我搜集了12 篇最新发表的关于KAN在时间序列预测领域的应用论文，并附上了开源代码链接，供大家学习和参考。对于有志于发表相关论文的同学们，我强烈建议你们深入研读这些文献。

三篇详述

1、KAN4TSF: Are KAN and KAN-based models Effective for Time Series Forecasting?

IMG_256

这篇文章探讨了将Kolmogorov-Arnold Network（KAN）应用于时间序列预测（Time Series Forecasting, TSF）任务的有效性。时间序列预测是一项基于历史数据预测变量未来值的关键任务，它在金融投资、天气预报、交通估计和健康管理等多个领域都有广泛应用。尽管现有的深度学习方法在时间序列预测方面取得了显著进展，但它们仍面临两大挑战：一是缺乏将网络规模与拟合能力联系起来的清晰数学理论；二是这些方法通常缺乏可解释性。

研究方法：

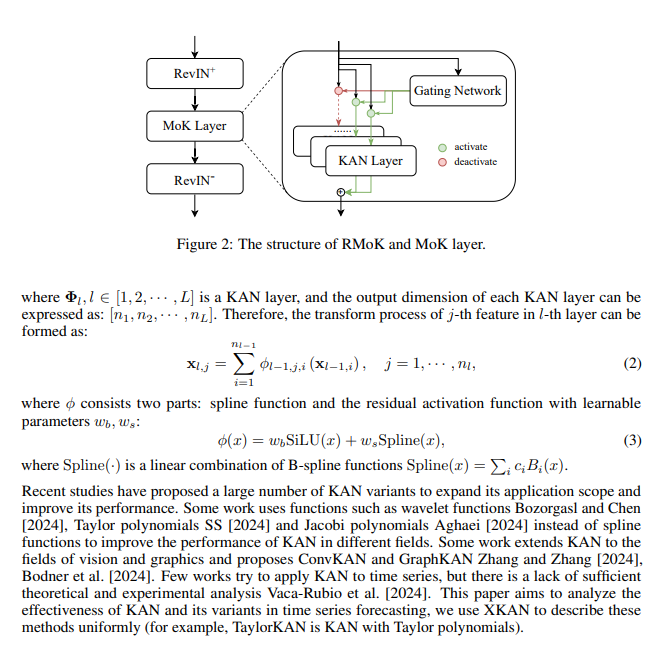
文章首先提出了一个基于KAN的时间序列预测模型，称为可逆混合KAN专家（Reversible Mixture of KAN Experts, RMoK）模型。RMoK使用混合专家结构，通过一个门控网络将变量分配给KAN专家进行预测。接着，文章通过在真实世界的数据集上比较RMoK与其他基线模型的性能、集成度和速度，来评估RMoK模型的有效性。

创新点：

混合KAN专家结构：文章提出了一种新颖的混合专家结构，该结构使用KAN变体作为专家，并用门控网络自适应地为特定专家分配变量进行预测。
可逆操作：RMoK模型采用了可逆的输入归一化和反归一化操作，以保持模型的简单性和可解释性。
门控网络的负载平衡：为了避免门控网络总是选择相同的几个专家，文章引入了一个负载平衡损失函数，鼓励专家之间的重要性均衡。

文章通过可视化技术特征权重与数据周期性之间的关系，探讨了RMoK模型的潜在机制，并得出了KAN和基于KAN的模型（RMoK）在时间序列预测中是有效的结论。

实验验证方面：

文章在七个真实世界的数据集上对RMoK模型进行了评估，并与多个流行的基线模型进行了比较。实验结果显示，在大多数情况下，RMoK模型都取得了最佳性能。此外，文章还探讨了将KAN集成到其他网络结构（如Transformer）中的可能性，并发现RMoK在多个数据集上的表现通常优于基线模型。

文章还讨论了KAN模型的效率问题，通过与其他基线模型的参数量和运行速度进行比较，发现KAN模型的运行速度受到特定实现方式的影响，但与线性模型相比，KAN模型在效率上有竞争力。

结论：

文章得出结论，KAN及其基于KAN的模型（RMoK）在时间序列预测任务中是有效的。RMoK模型不仅在性能上取得了优异的成绩，而且在解释性和集成度方面也展现出了优势。文章希望这项工作能为未来KAN模型在时间序列预测领域的研究提供帮助，以提高KAN模型的性能和可解释性。

2、Kolmogorov-Arnold Networks (KAN) for Time Series Classification and Robust Analysis

IMG_257

这篇文章研究了Kolmogorov-Arnold Networks（KAN）在时间序列分类（Time Series Classification, TSC）任务中的应用，并探讨了其在对抗性攻击下的鲁棒性。时间序列数据因其在多个领域的广泛应用，特别是在单变量时间序列分析中，为验证KAN提供了理想的实验场景。

研究方法：

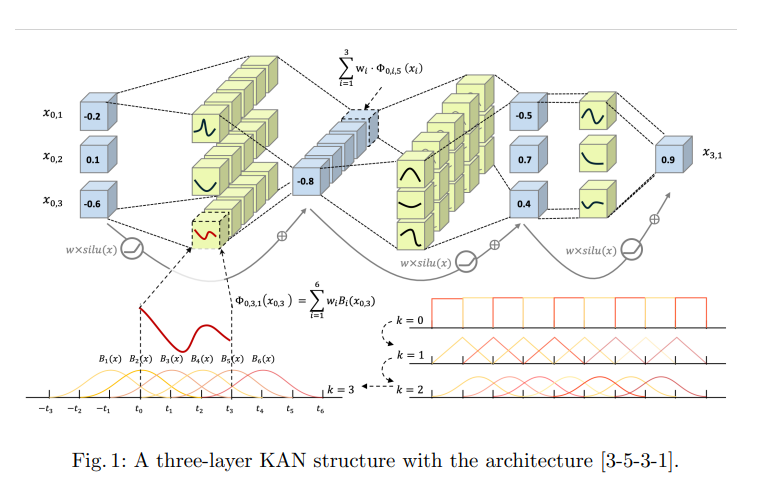
文章首先介绍了KAN的理论基础，即Kolmogorov-Arnold表示理论（KAT），该理论表明任何多变量连续函数都可以表示为单变量连续函数的有限组合。KAN的核心思想是将多层感知器（MLP）中的激活函数移到网络的边上，并通过这种方式来学习复杂的函数。

创新点：

KAN结构：文章提出了一种新的神经网络结构，即KAN，它与传统的MLP不同，通过在边上使用可学习的B样条函数作为激活函数，以适应不同的数据分布。
时间序列分类应用：文章将KAN应用于时间序列分类任务，这是一个新颖的尝试，因为KAN之前主要在物理领域内的公式构建中得到验证。
对抗性攻击下的鲁棒性分析：文章不仅关注KAN在时间序列分类中的性能，还研究了其在对抗性攻击下的鲁棒性，这是对KAN理论的一个重要补充。

文章通过在128个UCR数据集上进行公平比较，验证了KAN与MLP以及混合结构的性能。结果表明，KAN在多个数据集上达到了与MLP相当甚至略优的性能。

实验验证方面：

文章进行了消融研究，探讨了KAN中基础函数和B样条函数的作用。研究发现，输出值主要由基础函数决定，而B样条函数在没有基础函数的情况下难以优化。此外，文章还评估了KAN和其他模型的鲁棒性，发现KAN由于其较低的Lipschitz常数而展现出显著的鲁棒性优势。

结论：

文章得出KAN在时间序列分类任务中可以达到与传统MLP相媲美的性能，并且在对抗性攻击下表现出更强的鲁棒性。此外，文章还发现，具有较大网格尺寸的KAN表现出更大的鲁棒性，尽管它们的Lipschitz常数更高，这可能与B样条函数的值分布较小有关。

未来工作：

文章提出，未来的研究可以进一步探索KAN在其他领域的应用，并验证其在对抗性攻击下鲁棒性的异常现象。

总的来说，这篇文章通过将KAN应用于时间序列分类任务，并对其鲁棒性进行分析，为神经网络的理论基础和实际应用提供了新的视角和实验依据。

3、Deep State Space Recurrent Neural Networks for Time Series Forecasting

IMG_258

这篇文章提出了一种新颖的神经网络框架，用于时间序列预测，特别是在加密货币市场动态建模方面。文章的核心贡献在于将计量经济学中的状态空间模型原理与循环神经网络（RNNs）的动态能力相结合，提出了一种结合了状态空间模型和RNNs的深度学习方法。

研究方法：

文章首先介绍了几种用于时间序列预测的神经网络架构，包括长短期记忆网络（LSTM）、门控循环单元（GRU）和时间 Kolmogorov-Arnold 网络（TKAN）。这些模型被设计为能够处理时间序列数据的复杂依赖性，并且能够捕捉到加密货币市场的独特和复杂动态。

创新点：

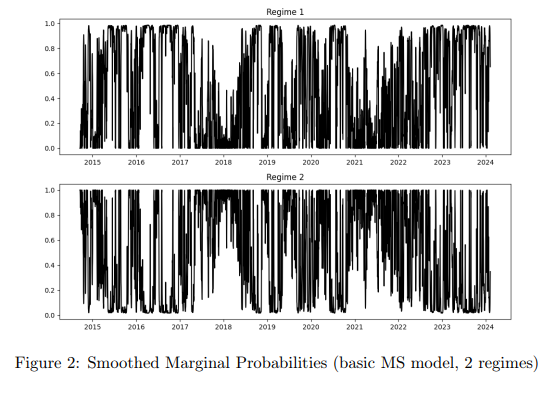
状态空间模型与RNNs的结合：文章提出了一种新的方法，将状态空间模型与RNNs结合，通过实现一个隐藏的切换机制，允许模型在多个网络之间切换，其中转换概率随时间变化，并受到某些可观测协变量的影响。
深度状态空间模型：提出了一种深度状态空间模型，该模型使用LSTM、GRU和TKAN作为状态空间模型的基础，通过引入隐藏的马尔可夫链来模拟市场状态的变化。
时间变转换概率：文章提出了一种估计时间变化转换概率的新方法，该方法使用神经网络来估计状态转换概率，从而允许模型动态地适应时间序列数据的变化。

文章通过在多个真实世界的数据集上进行模拟实验，验证了所提出方法的有效性。实验结果表明，TKAN在大多数情况下都取得了最佳性能，这表明了该方法在处理具有挑战性的序列数据预测任务时的有效性。

实验验证方面：

文章通过在包括比特币在内的多个加密货币数据集上进行实验，展示了所提出模型在预测市场状态方面的能力。实验中，使用了不同的评估指标，如精确度、召回率、F1分数和支持度等，来评估模型的性能。实验结果表明，与传统的RNN模型相比，提出的带有状态空间模型的RNN模型（即m-GRU、m-LSTM和m-TKAN）在预测准确性和风险管理方面都有显著提升。