【轨迹生成】参数化最优控制 约束-控制-图形参数

Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control

Alonzo Kelly
Bryan Nagy

---

---

1. 车辆的运动模型

• 车辆运动描述
  

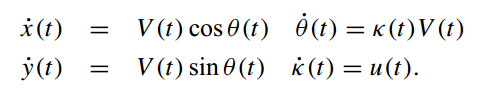
• 车辆状态
  

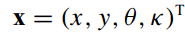
• 控制输入–决定速度和曲率变化
  

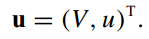
• 换元得到距离s的函数
  
  
  

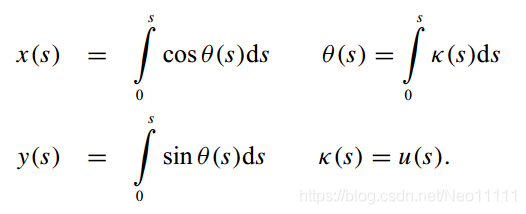
2. 轨迹最优化问题

给定起点、目标点的状态（包括位姿、曲率，也可以包括速度）等，找到一个合适的控制输入，产生相应的轨迹，且轨迹需要满足动态模型的约束、且不触碰障碍物。这样的控制输入可能不存在，也可能存在，甚至存在多个，那么需要从多个合乎要求的控制输入中找到最优控制。

3. 最优化控制公式

• 非线性系统运动方程
  
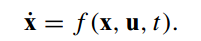
• 评估函数，可以看出它与末状态及整条路径的情况有关，我们的最优化问题实际上是使J函数最小化
  
• 起点和目标点需要满足的约束
  
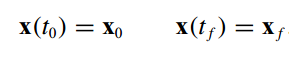
• 控制输入有界，其变化速度也有界，约束如下
  

4. 问题转化–服从约束条件的最优解

• 引入参数p，p为和轨迹形状相关的一系列参数，那么它自然将决定各时刻的控制输入，即
  

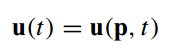
• 由于控制u将决定状态x，且二者共同决定$\dot{x}$，那么此时$\dot{x}$将由参数p决定
  

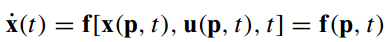
• 将起点与目标点（甚至可以使轨迹上的一系列指定要到达的点）称为边界状态，由初始状态加上$\dot{x}$的积分得到，其值需要与我们的要求（表示为$x_b，$向量）相等
  

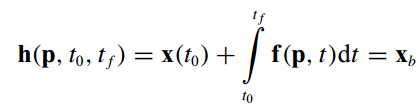
• 将上式变形如下，得到边界条件约束的标准形式
  

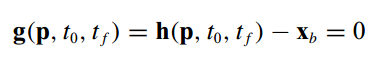
• 那么轨迹最优化可以公式化描述如下，即服从g=0约束条件下的J函数最小化问题（且参数p有界）
  
  

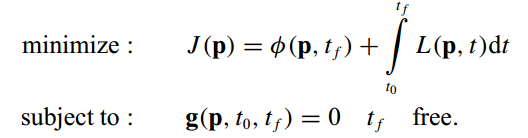
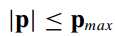
• 换元，q是包含p和s的向量，进一步地，上述最优化公式可以写为
  
  

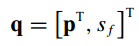
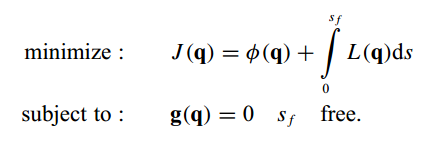
5. 拉格朗日乘数法求解–有约束条件的多元函数极值

• 用J和约束g构造构造拉格朗日函数
  

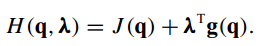
• 极值条件需要满足H对q和λ的偏导数之和=0
  
  

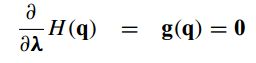
• 上式变形（f(x)=0=>f(x)+f’(x)△x=0）
  
  

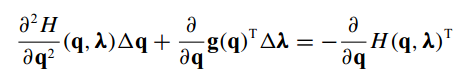
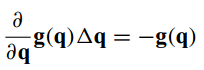
• 矩阵形式
  

• 实际上相当于令J对q的偏导数和g对q的偏导数分别=0，前者体现无约束条件的最优化，后者体现约束条件。

6. 例:螺旋曲线Clothoids 和多项式曲线Polynomial Spirals

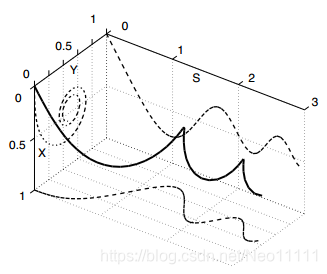
• 螺旋曲线
  可以发现，当产生螺旋曲线式的轨迹时，有两个参数a、b，当s=0即起始点处，曲率为a，随着s的增大，曲率以b的速度增加。然而这样的曲线参数太少，当给定了起点的曲率和目标点位置时，无法保证目标点处的曲率满足要求，甚至连朝向都不一定能满足。
  
  

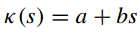
• 多项式曲线
  多项式曲线的参数更多，可以满足更多的边界条件
  
  

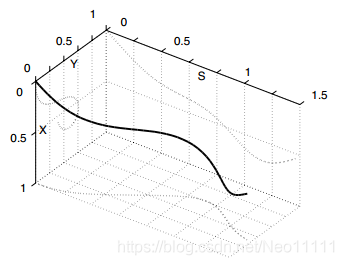
给出控制的形式后，很容易通过积分运算得到朝向、x、y随s的变化（这里默认起点位置0,0，朝向0）


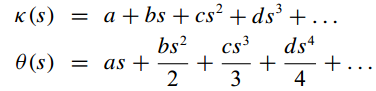
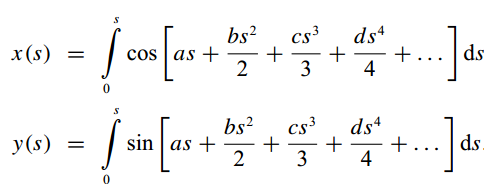
假设我们总共需要满足的边界条件有8个：

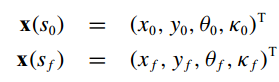
而在通过积分构造，默认$x_0、y_0、{\Theta }_0=0$，故前三个约束是自然满足的，还剩五个约束需要去满足，即$k_0、x_f、y_f、{\Theta }_f、k_f$

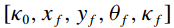
而恰好有五个参数

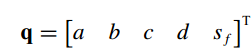
首先考虑$k_0$，将s=0带入k(s)，即可得到，要满足$k_0$的约束只需

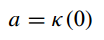
对于剩下四个边界条件：

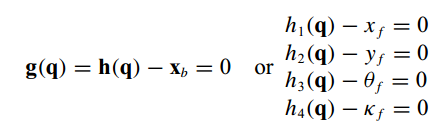
7. 评价函数J的设计

1) 边界条件可以不作为约束，而体现在J中

对于轨迹上某个点的要求，体现在$\varphi$函数的设计上

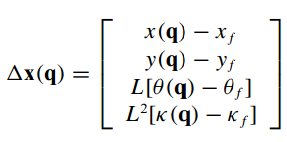
2) 希望轨迹更平滑

对于整条轨迹的要求，体现在L函数上