基于最优控制的路径规划算法

一、算法基本步骤

1.根据传感器及道路边界，生成可行驶区域ROI

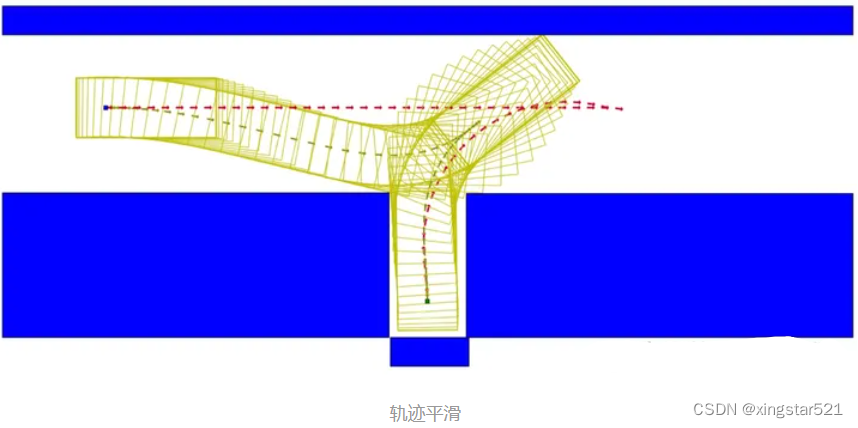
2. Hybird A* + RS曲线规划出一条粗糙的轨迹, 求出一个没有碰撞的参考解. 这条粗糙的轨迹可能会存在曲率突变, 这是不满足车辆的运动学要求的.

3. IAPS或者OBCA算法对轨迹进行进一步的平滑以满足车辆控制的需求. 图示中, 红色虚线是粗糙轨迹, 绿色虚线是平滑后的轨迹

2.OBCA算法 

 作用：对于原始路径存在的折线、不符合车辆运动学的问题，需要进一步平滑处理。来满足控制和乘坐舒适性的要求。

OBCA算法基于模型预测控制（MPC）建立模型，并用优化算法进行求解。它有如下几点优势： 

• 可以加入障碍物约束. 这一点和RS曲线的解析求解不同, RS虽然可以求出最优的解析解, 但是没有办法考虑障碍物的碰撞的约束.
• 可以产生满足车辆运动学约束(曲率连续变化)的轨迹.
• 可以实现横纵向的联合规划(同时考虑速度对路径的影响)

2.1.MPC预测模型

 下图展示了模型预测控制MPC：

 

模型预测控制会通过一个采样时间将未来时域离散成多段, 在给定控制模型和参考值曲线, 计算使预测输出与实际输出最接近的输入序列, 并将输入的第一个分量作用于系统. 

MPC问题→优化问题

        1：首先设计目标函数（约束）

        2：对未来状态进行优化求解

即设计MPC的预测模型。

车辆的运动学模型的示意图如下图所示： 

首先定义自车的状态变量, 包括自车第  时间的在笛卡尔坐标系下的坐标 , 车速  , 航向角theta 

. 

 

总结就是：知道第一个状态的位置信息和运动信息 就能得到下一状态的状态信息

 2.2.MPC约束设计

2.2.1.规划的轨迹和障碍物保持一定距离

2.2.2.规划的轨迹起点和终点满足给定的状态

2.2.3.状态的迭代满足运动学约束

2.2.4状态量满足车辆极限

2.2.5输入量满足车辆极限 

2.3.MPC目标函数设计 

2.3.1.跟踪参考路径变化

2.3.2.加速度尽可能小

2.3.3.第一个输入分量和当前状态输入尽可能接近

2.3.4.输入量变化率尽可能小