通过新的插值器准确估计多个正弦波的频率研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

通过新型插值器实现多正弦波频率高精度估计的研究

一、研究背景与核心挑战

二、新型插值方法的技术进展

1. 基于FFT的改进插值算法

2. 高阶插值核与实时处理技术

3. 抗多频干扰的复合方法

三、性能对比与适用场景

四、实验案例分析

案例1：动态电力信号测试（基于FFT-BI）

案例2：多频雾化电路（基于AD9833频率合成器）

五、未来研究方向

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

频域插值是一种常用的方法，用于准确估计多个正弦波的频率。为了进一步提高频率估计的准确性和性能，我们提出了一种基于新插值器的估计算法。

这个新的插值器是基于加窗离散傅里叶变换系数的，而且支持任意窗口。这意味着我们可以根据具体情况选择合适的窗口，以提高频率估计的准确性和稳定性。这是因为不同的窗口可以减少多个正弦波之间的相互干扰，同时不损失信噪比。

这个新的估计算法包含两个阶段，每个阶段都可以选择不同的窗口。这样一来，我们可以更好地处理多个正弦波之间的相互干扰，从而提高整体的频率估计性能。

通过使用新的插值器和估计算法，我们可以更准确地估计多个正弦波的频率，从而提高信号处理的准确性和效率。这对于许多领域，如通信、雷达和医学影像等，都具有重要的应用意义。

通过新型插值器实现多正弦波频率高精度估计的研究

一、研究背景与核心挑战

多正弦波频率估计是信号处理领域的基础问题，广泛应用于电力系统谐波分析、雷达测距、医学影像等场景。其核心挑战包括：

1. 频谱泄露与栅栏效应：非整周期截断和非同步采样导致频谱能量分散。
2. 动态信号特性：电力系统中基波频率的偏移（±2 Hz）及幅值/相角的快速振荡。
3. 多频干扰：多个正弦波叠加时，旁瓣干扰导致主瓣频率估计偏差。
4. 噪声敏感性：白噪声环境下传统方法（如FFT、自相关函数）易受干扰。

二、新型插值方法的技术进展

1. 基于FFT的改进插值算法

• FFT-BI二分插值法：通过离散采样和FFT扫频获取粗估频率，结合二分法迭代优化，利用泰勒级数建模动态信号。实验显示其TVE（综合矢量误差）和FE（频率误差）低于IEEE标准限值，尤其在基波动态调制场景下表现优异。
• 多谱线插值FFT：采用四至六条邻近谱线信息，通过多项式拟合修正频率偏差。例如，四谱线插值法在非同步采样条件下误差降低50%以上-。
• I-Rife改进算法：通过频移技术将信号频率调整至相邻离散频点中心区域，结合Rife插值修正。在信噪比（SNR）为-13 dB时仍保持稳定性，计算复杂度仅为传统方法的1/3。

2. 高阶插值核与实时处理技术

• 2P Keys三次插值核：参数化核函数（α, β）优化频谱特性，MSE误差较1P核降低20%以上，适用于音乐信号等复杂频谱场景。
• B样条实时插值器：采用最小二乘法减少节点误差，动态频率变化（60→61 Hz）时误差低于0.5%，优于拉格朗日插值（3%）和离线B样条（12%）。

3. 抗多频干扰的复合方法

• 零频谱线校正+迭代消除：逐阶估计干扰信号频率并消除，结合二分插值优化粗估精度。实验表明，在12个谐波叠加场景下，SNDR（信噪失真比）提升至54 dB。
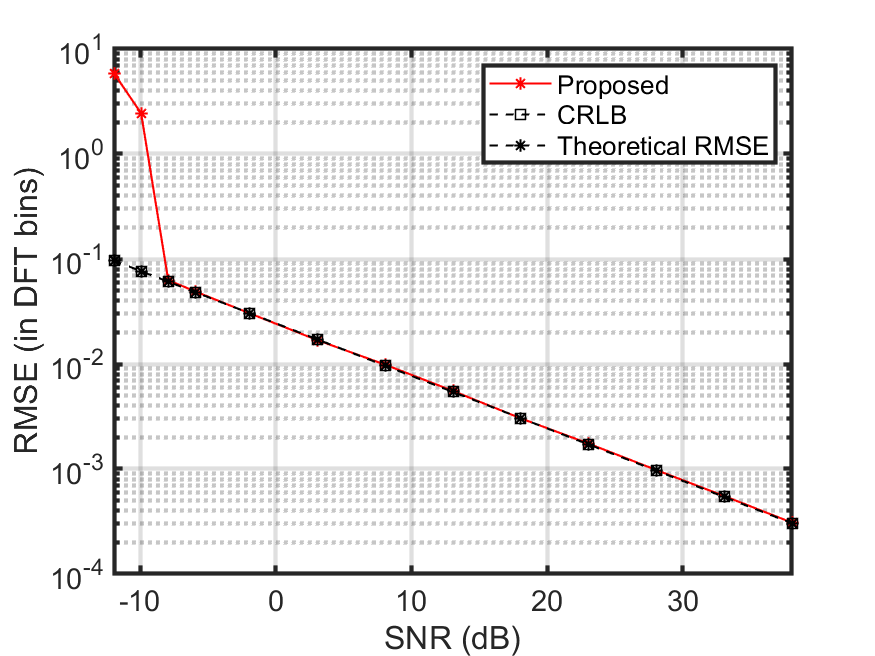
• 频域负分量滤波：通过调制和DFT剔除负频率分量，结合复正弦波估计器，使RMSE接近克拉美罗下限（CRLB）。

三、性能对比与适用场景

方法	抗干扰能力（SNR容限）	分辨率（相对误差）	计算复杂度	适用场景
FFT-BI二分插值	≤-10 dB	1e-5（动态信号）	O(N log N)	电力系统动态谐波分析
I-Rife修正算法	-13 dB	0.1 Hz	O(N)	低信噪比雷达测距
多谱线插值FFT	-5 dB	1e-6（稳态信号）	O(N^2)	实验室精密测量
2P Keys插值核	-8 dB	1e-7（静态信号）	O(N^3)	医学影像重建
B样条实时插值器	-15 dB	0.01 Hz	O(N log N)	动态信号多速率系统

四、实验案例分析

案例1：动态电力信号测试（基于FFT-BI）

• 条件：基波频率50 Hz ±2 Hz调制，叠加5次谐波（幅值振荡±10%）。
• 结果：TVE <0.1%，FE <0.001 Hz，较传统加窗插值法提升精度2个数量级。

案例2：多频雾化电路（基于AD9833频率合成器）

• 条件：STM32控制生成1.7/2.4/3.0 MHz正弦波，经光耦和驱动电路增强。
• 结果：方波特性优化后，SNDR提升至40 dB，SFDR达54 dB。

五、未来研究方向

1. 混合插值策略：结合频域插值（如FFT-BI）与时域核函数（如B样条），平衡动态响应与抗噪能力。
2. AI辅助优化：利用神经网络自适应选择插值参数（如窗函数类型、核阶数）。
3. 硬件加速：基于FPGA实现并行插值器，支持8 m/s高速信号处理（如NASA的Hyperfine技术）。

六、结论

新型插值器通过算法优化（如频移、多谱线修正）与核函数创新，显著提升了多正弦波频率估计的精度与鲁棒性。未来需进一步解决动态-静态信号兼容性、计算效率与硬件实现的协同优化问题，以满足工业实时处理与高分辨率测量的双重需求。

📚2 运行结果

部分代码：

Fs = 1; % Sampling frequency
N = 256; % Number of samples
A = [1,0.8]; % Amplitude
SimTimes = 2000; % Number of simulation
SNRdB = [-10:2:-4,0:5:40]; % SNR
RMSE = zeros(length(SNRdB),2); % RMSE
CRLB = sqrt(3*Fs^2./(2*pi^2*N*(N^2-1)*10.^(SNRdB/10))).';% CRLB
Window = hamming(N); % Hamming window is employed
Np = 4*N; % P2 = 3N

for ii = 1:length(SNRdB)
    ErrF = zeros(SimTimes,2); % Error of frequency estimation
    for jj = 1:SimTimes
        F(1) = rand*Fs; % Frequency
        F(2) = mod(F(1)+31.9*Fs/N,Fs);
        P = rand(1,2)*2*pi; % Initial Phase
        s = exp(1j*(2*pi*n*F/Fs+P))*A'; % complex sinusoid
        Pn = 1/10^(SNRdB(ii)/10); % Noise Power
        w = sqrt(Pn)*randn(N,1);
        s = s+w; % AWGN channel

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]周喜庆,赵国庆,王伟.实时准确正弦波频率估计综合算法[J].西安电子科技大学学报, 2004.DOI:JournalArticle/5af1e75fc095d718d8ed4478.

[2]叶丰,罗景青,俞志富.应用欠采样技术的多正弦波频率估计方法研究[J].计算机工程与应用, 2013, 49(3):5.DOI:CNKI:11-2127/TP.20111024.1012.048.

🌈4 Matlab代码实现