【核心复现】模拟风电不确定性——拉丁超立方抽样生成及缩减场景研究（Matlab全代码）

于 2025-05-02 13:18:59 发布
阅读量492 收藏 22
点赞数 23
文章标签： matlab 人工智能 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Yan_she_He/article/details/147662470
版权

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

模拟风电不确定性的拉丁超立方抽样生成及缩减场景研究

一、研究背景与核心问题

二、拉丁超立方抽样的基本原理

1. 与蒙特卡洛抽样的对比

2. LHS的数学步骤

三、风电不确定性建模与场景生成

1. 预测误差分布假设

2. 场景生成参数设置

四、场景缩减技术

1. 主要方法分类

2. 改进方向

五、案例分析与应用

1. 综合能源系统调度

2. 风储混合系统优化

六、研究进展与挑战

七、核心复现文档撰写规范

八、结论

📚2 运行结果

2.1 场景生成

2.2 场景削减

🎉3 参考文献

🌈4 Matlab代码、数据

💥1 概述

模拟风电不确定性的拉丁超立方抽样生成及缩减场景研究

拉丁超立方抽样（Latin Hypercube Sampling, LHS）作为一种统计抽样技术，广泛应用于不确定性分析和风电模拟领域。该方法通过高效生成样本空间内的代表点，能够有效模拟和研究风电输出的不确定性。下面，我们将通过几个步骤解释如何使用拉丁超立方抽样（LHS）来模拟风电的不确定性，并介绍场景缩减技术以提高计算效率。

一、研究背景与核心问题

风电出力受风速随机性、预测误差等因素影响，具有显著的不确定性。为量化这种不确定性，需通过场景分析法生成大量可能的风电出力场景，并缩减为典型场景集，以优化电力系统规划和运行。拉丁超立方抽样（Latin Hypercube Sampling, LHS）因其分层抽样特性，能够高效覆盖样本空间，成为风电不确定性模拟的核心方法。

二、拉丁超立方抽样的基本原理
1. 与蒙特卡洛抽样的对比
  • 蒙特卡洛：简单随机抽样，样本易聚集，需大量样本才能覆盖分布范围，计算成本高。
  • 拉丁超立方：分层抽样，将变量范围划分为等概率区间，每个区间仅抽取一个样本，保证均匀覆盖。相比蒙特卡洛，LHS能以更少样本准确反映分布特性，减少计算时间和存储需求。
2. LHS的数学步骤
  1. 分层划分：将预测误差的概率分布分为NN个等概率区间（如正态分布分为N=1000N=1000个区间）。
  2. 区间内采样：对每个区间随机抽取一点​，其中r∈[0,1]为随机数。
  3. 反函数变换：通过累积分布函数（CDF）的反函数F−1(pi)生成服从目标分布的样本值。
  4. 随机排列：对各维样本独立排序后组合，避免维度间相关性导致的偏差。
三、风电不确定性建模与场景生成
1. 预测误差分布假设
2. 场景生成参数设置
  • 典型参数：时间周期Z=24Z=24小时，抽样次数iterations=1000iterations=1000，代表性场景数S=5S=5（缩减后）。

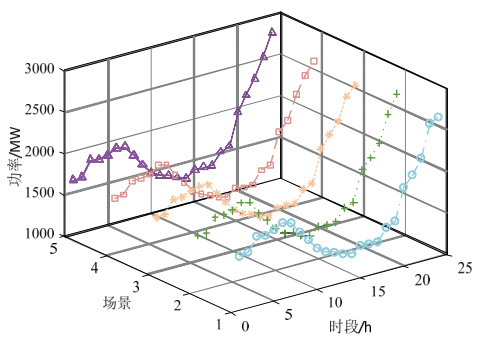
  • 多维扩展：考虑多风电场相关性时，采用Sobol序列增强的LHS（SaLHS）或Copula函数处理时空相关性。
四、场景缩减技术
1. 主要方法分类
方法类型算法示例特点与适用场景
概率距离法快速前代消除法（FFS）基于Kantorovich距离，合并概率相近场景
聚类法K-means按几何相似性聚类，保留簇中心作为典型场景
同步回代法SBR迭代合并最小概率距离的场景，全局最优性高
混合方法K-means + SBR结合聚类和概率距离，兼顾效率与精度
2. 改进方向
  • 三维距离度量：在SBR中引入相关性、量级和形态的三维距离，提升相似性评估全面性。
  • 趋势拟合：提取场景的时间趋势特征，减少随机噪声干扰，适用于风资源分析。
五、案例分析与应用
1. 综合能源系统调度
  • 场景生成：基于LHS生成1000个风电出力场景，假设服从正态分布，缩减至5个典型场景（图C3）。
  • 优化效果：典型场景覆盖实际出力波动范围，支撑系统低碳经济调度。
2. 风储混合系统优化
  • 风速建模：ARMA模型预测风速，LHS生成误差场景，缩减后得到有限出力场景及概率。
  • 结果验证：LHS场景分布均匀，显著优于蒙特卡洛的样本聚集问题（图3 vs. 图2）。
六、研究进展与挑战
  1. 多维度相关性处理：SaLHS结合D-vine Copula，提升多风电场时空相关性建模精度。
  2. 问题驱动缩减：将随机优化目标融入场景缩减，通过MILP最小化优化差距。
  3. 评估指标创新：引入覆盖性指标（PA、PB）和形态相似性度量，量化场景代表性。
七、核心复现文档撰写规范
  1. 方法描述：明确分布假设（如正态分布参数σ=10%Pforecastσ=10%Pforecast​）、LHS分层步骤、缩减算法（如SBR迭代过程）。
  2. 代码与数据：提供Matlab/Python代码（含注释）、输入数据格式（如24小时预测值）、关键参数设置（如N=1000N=1000）。
  3. 可复现性：附数据集、反函数计算细节（如威布尔参数c,kc,k公式）及缩减过程日志文件。
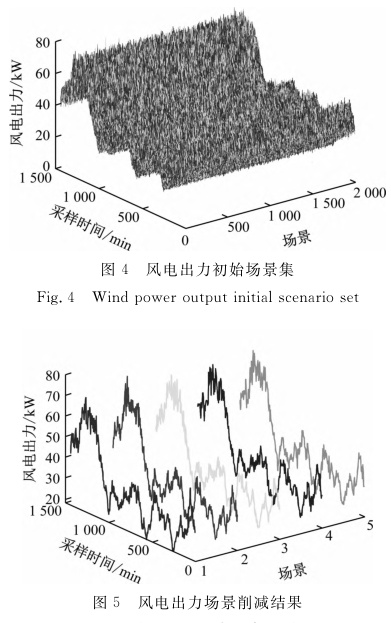
  4. 结果对比：展示初始场景与缩减场景的分布对比图（如2000→5场景），量化覆盖性指标。

八、结论

拉丁超立方抽样结合场景缩减技术，为风电不确定性建模提供了高效解决方案。未来研究需进一步探索多维相关性建模、动态趋势适应性及与优化模型的深度耦合。复现研究需注重方法透明性、代码可读性及结果验证，以支撑电力系统的高效决策。

📚2 运行结果

研究表明，风电出力的不确定性主要源于预测误差。据分析，这种误差（通常用符号 e 表示）服从正态分布，并且大致相当于预测出力的10%。为了更好地理解和应对这一不确定性，我们采用了拉丁超立方抽样方法实现了场景生成[1]，同时借助基于概率距离的快速前代消除法进行了场景缩减[2]。这样的操作使我们能够更有效地模拟风电出力的不确定性，并为相关决策提供更可靠的依据。

2.1 场景生成

2.2 场景削减

部分代码：

%% 场景生成
% 概率密度函数
y1 = @(x) exp(-(x-mu)^2/(2*sigma^2))/(sigma*(2*pi)^0.5);
% 累计分布函数
CDF = @(x)@(mu)@(sigma) normcdf(x,mu,sigma);
x = leng : 0.1 : leng;
y2 = CDF(x);
% 拉丁超立方抽原始样本
segmentSize = 1 / iterations;                                              % 每层大小
for j = 1:Z
for i = 0 : iterations-1                                                   % 逐层随机抽样 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]蒋程,王硕,王宝庆,等.基于拉丁超立方采样的含风电电力系统的概率可靠性评估[J].电工技术学报,2016,31(10):193-206.DOI:10.19595/j.cnki.1000-6753.tces.2016.10.023.

[2]董文略,王群,杨莉.含风光水的虚拟电厂与配电公司协调调度模型[J].电力系统自动化,2015,39(09):75-81+207.

🌈4 Matlab代码、数据

论文复现：模拟风电不确定性——拉丁超立方抽样生成及缩减场景（Matlab全代码）
WW、forever的博客
02-20 6108
采用拉丁超立方抽样实现场景生成、基于概率距离的快速前代消除法实现场景缩减，以此模拟风电出力的不确定性
模拟光伏不确定性——拉丁超立方抽样生成及缩减场景（Matlab全代码）
WW、forever的博客
03-01 3725
光伏出力的不确定性主要源于预测误差，与风电不确定性模拟在于——在不确定模拟中光伏存在0出力点，容易出现超出索引范围的情况，本代码解决了该问题。
【MATLAB第100期】基于MATLAB的多种改进拉丁超立方LHS数据抽样方法
随风飘摇的土木狗的博客
03-10 4285
介绍三种LHS方法，包括LHS、OLHS、TPLHS。其中，LHS及TPLHS支持在限定范围取值，而GAOLS、ESEAOLHS只适用于0-1范围内抽样取值。
拉丁超立方体抽样（LHS）研究（Matlab代码实现）
weixin_46039719的博客
12-17 7205
拉丁超立方体抽样（LHS）是一种分层随机过程，提供了一种从变量分布中抽样变量的有效方法（Iman和Conover，1980）。Xk中的每一个的规定分布中采样ns值。每个变量的累积分布被划分为N个等概率区间。从每个间隔中随机选择一个值（图1）。为每个变量获得的N个值与其他变量随机配对。与简单的随机抽样不同，该方法通过最大程度地分层每个边际分布，确保了每个变量范围的完全覆盖。博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。部分理论来源于网络，如有侵权请联系删除。详细文章讲解见第3部分。行百里者，半于九十。
Matlab 拉丁超立方采样lhsdesign函数、lhsnorm函数介绍
热门推荐
Bulander的博客
04-08 3万+
本文主要介绍了Matlab自带的两个拉丁超立方抽样的两个函数——lhsdesign函数、lhsnorm函数，拉丁超立方抽样的原理后面有时间写一篇文章介绍一下 假设我们现在想对10000个人进行抽样，我们只关心人的身高、体重这两个维度，现在用拉丁超立方抽样法从这10000个人中抽出40个样本。 lhsdesign函数 X = lhsdesign(n, p); lhsdesign函数是基本的拉丁超立方抽样的函数，总体的抽样结果服从均匀分布，返回一个 n×pn \times pn×p 的矩阵，每一列的元素是随机
Matlab拉丁超立方抽样（与Cholesky 分解法重排序）
Liao_223的博客
03-25 2675
对6个随机变量进行拉丁超立方抽样：3个正态分布随机变量：, , 3个均匀分布随机变量：要点：调用matlab中的lhsnorm()函数进行正态分布抽样，lhsdesign()函数进行均匀分布抽样。代码中Xrms为抽样矩阵的相关系数矩阵方均根，用于衡量不同变量列之间的相关性，相关性越低越好。注意：输出结果已经被重排，相关性较低。 输出画图结果 为了使得抽样结果更加具有代表性，需要降低不同变量列之间的相关性，即对列中的元素进行重排列。方法有：Gram-Schmidt序列正交化方法、Cholesky分解法和
【核心复现】模拟风电不确定性——拉丁超立方抽样生成及缩减场景研究附Matlab代码.rar
最新发布
04-27
.版本：matlab2014/2019a/2024a ...3.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。 4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
【核心复现】模拟负荷不确定性——拉丁超立方抽样生成及缩减场景研究（Matlab全代码）
q216605q的博客
01-24 1101
模拟负荷不确定性是电力系统规划和运行中的重要问题之一。拉丁超立方抽样（Latin Hypercube Sampling, LHS）是一种常用的统计方法，用于生成具有一定分布特征的随机样本，可以用于模拟负荷不确定性。本文通过对LHS方法的应用，研究模拟负荷不确定性的场景生成和缩减问题。首先，我们利用LHS方法生成具有一定分布特征的负荷随机样本。具体来说，我们可以根据历史负荷数据的统计特征（如均值、标准差、相关性等）来设定LHS抽样的参数，从而生成符合实际情况的负荷场景。
基于拉丁超立方抽样和样本削减的风光出力及负荷场景预测分析
05-10
通过这种方式，我们可以模拟出各种可能的气象场景，以评估风光发电的不确定性。 样本削减是处理大数据集时常用的一种策略，它可以降低计算复杂性，同时保持模型的预测性能。在风光出力预测中，原始数据可能包含大量...
拉丁超立方体抽样matlab
03-19
拉丁超立方体抽样matlab代码，contents.m里有说明。
20超拉丁立方抽样matlab-latin-sampling
04-28
20超拉丁立方抽样matlab-latin-sampling
matlab 拉丁超立方抽样LHS.m
09-17
拉丁超立方抽样 %code of Latin Hypercube Sampling% %call S=lhs(m,dist,mu,sigma,lowb,upb) % %Input argument %m: a scalar,the number of sample points %dist: A row with distribution type flags of basic random variables;the %value of the flag can be 1 (for uniform distribution, 2(for normal distribution), 3(for
拉丁超立方MATLAB程序
10-12
拉丁超立方试验设计方法，可根据给定参数的范围生成设计矩阵
拉丁超立方抽样 matlab代码
02-25
拉丁超立方的抽样程序，任意维度，任意抽样范围，及抽样个数设置
拉丁超立方抽样法（LHS）matlab程序，包含正态分布，对数正态分布等
weixin_43660798的博客
07-06 3万+
对LHS介绍的可以参考：https://blog.csdn.net/Together_CZ/article/details/90076271 下面是4种分布的matlab程序，包含正态分布，均匀分布， 对数正态分布，extreme type 1。 1.对正态（高斯）分布的变量进行拉丁超立方采样 参考：https://blog.csdn.net/chichuhe/article/details/89...
LHS拉丁超立方采样matlab程序，对于均匀分布与正态（高斯）分布的变量进行拉丁超立方采样
Kevin的小屋
05-06 2万+
1、对正态（高斯）分布的变量进行拉丁超立方采样 clc clear all close all cst_Mu_Sigma = load( 'cst_Mu_Sigma.dat'); Mu = cst_Mu_Sigma(:,1); Sigma = cst_Mu_Sigma(:,2); D = size(Mu,1); % 维数 Covariance_Matrix = zeros(D,D); for...
超拉丁立方采样示例程序
01-03
超拉丁立方采样的MATLAB示例程序。改抽样方法相较于蒙特卡洛抽样方法具有更高的效率，更快的速度，并且能够分析样本之间的相关性。
图解拉丁超立方抽样
qq_41710383的博客
03-06 3万+
拉丁超立方抽样 1.拉丁超立方抽样 拉丁超立方抽样技术最早于1979年由McKay等提出，该方法具有以下优点： 具有均匀分层的特性 可以通过该抽样，得到尾部的样本值 以上两点使得拉丁超立方抽样比起普通的抽样方法更加的高效。 2拉丁超立方抽样的步骤 首先确定样本数N，既要抽取的样本数目 将（0，1）区间均分为N段 在这M段中的每一段随机的抽取一个值 将抽取的值通过标准正态分布的反函数映射为标准正态分布样本 打乱抽样顺序，用matlab中的sort函数 通过以上四步便完成了拉丁超立方抽样 3图解拉丁超立
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值