自动控制原理第二章（控制系统的数学模型）【上】

Zevalin爱灰灰

已于 2024-11-01 22:54:44 修改

阅读量1.8k

点赞数 30

分类专栏：自动控制原理文章标签：信号与系统自动控制原理

于 2024-10-28 23:43:08 首次发布

本文链接：https://blog.csdn.net/Zevalin/article/details/143316031

版权

自动控制原理专栏收录该内容

16 篇文章

订阅专栏

一、概述

控制系统的数学模型，是描述系统输入、输出变量以及内部各变量之间关系的数学表达式。

建立控制系统的数学模型，通常采用解析法和实验法。

①解析法是对系统各部分的运动机理进行分析，根据所依据的物理规律或化学规律分别列写相应的运动方程。

②实验法是人为地给系统施加某种测试信号，记录其输出响应，并用适当的数学模型去逼近，这种方法又称为系统辨识。

二、控制系统的数学模型—微分方程

1、线性定常系统微分方程的一般形式

（1）线性定常系统微分方程的一般形式如下，各信号项的系数均与时间无关，且方程中没有信号交叉乘积项或常数项。

（2）线性定常系统满足叠加定理，如下图所示。

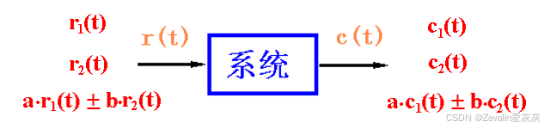
2、线性元部件、线性系统微分方程的建立

（1）用解析法列写系统或元部件微分方程的一般步骤：

①根据系统的具体工作情况，确定系统或元部件的输入、输出变量。

②从输入端开始，按照信号的传递顺序，依据各变量所遵循的物理（或化学）定律，列写出各元部件的动态方程，通常是一组微分方程。

③联立方程消去中间变量，写出关于输入、输出变量的微分方程式。

④将微分方程标准化，即将与输入有关的各项放在等号右侧，与输出有关的各项放在等号左侧，并按从高阶导数到低阶导数顺序排列。

（2）举例：

①R-L-C无源网络如下图所示，其中R、L、C分别是电路的电阻、电感和电容值。

②弹簧-质量-阻尼器系统如下图所示，其中K为弹簧的弹性系数，f为阻尼器的阻尼系数，m表示小车的质量，忽略小车与地面的摩擦， $y(t)$ 为小车的位移。

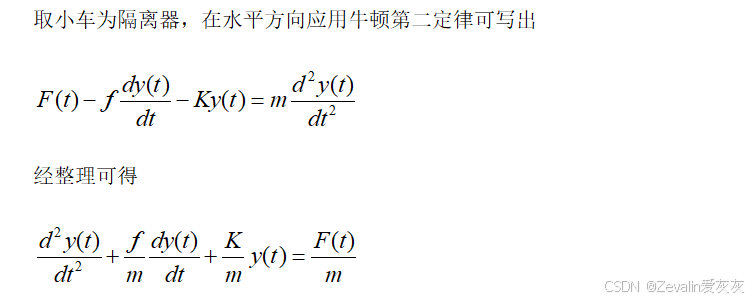
③电枢控制式直流电机的工作原理如下图所示，电枢电压 $u_{a}(t)$ 为输入量，电动机转速 $\omega (t)$ 为输出量， $R_{a}$ 、 $L_{a}$ 分别是电枢电路的电阻和电感， $f_{m}$ 、 $J_{m}$ 分别是折合到电动机轴上的总粘性摩擦系数和总转动惯量，激磁电路 $i_{f}$ 视作常值。

3、非线性系统微分方程的线性化

（1）前面讨论的元件和系统，假设都是线性的，描述它们的数学模型也都是线性微分方程，然而事实上任何一个元件或系统总是存在一定程度的非线性。如果通过某些近似化简或适当限制问题的研究范围，可以将大部分线性方程在一定的工作范围内近似用线性方程来代替，这就是非线性特性的线性化，这样就可以用线性理论在分析和设计系统。

（2）举例：

4、拉氏变换的回顾与借助拉氏变换求解线性定常微分方程

（1）借助拉氏变换，可以将微分方程变换成复数域的代数方程，求解代数方程后进行拉氏反变换，即可得到微分方程的解析解。（整个过程通常借助拉氏变换的重要性质）

（2）常见的拉氏变换：

（3）拉氏变换的几个重要性质：

（4）用拉式变换方法解线性常微分方程，如下所示，其中c为输出信号（参数t省略），n＞m（信号关于时间的导数阶数），r为输入信号（参数t省略），初始条件为0。

（5）用留数法分解部分分式：

①一般情况：

②举例：

（6）线性定常微分方程求解举例：

5、运动的模态

（1）线性微分方程的解由齐次方程的通解和给定信号对应的特解组成，通解反映系统自由运动的规律。

（2）一个系统确定以后，它的闭环极点（特征根）也就确定，这个系统对应的模态也就随之确定了。

（3）每一种模态可以看成是线性系统自由响应最基本的运动形态，线性系统的自由响应就是其相应模态的线性组合。

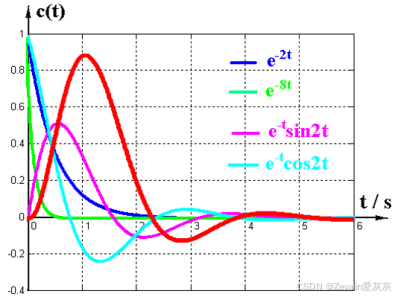
三、控制系统的复域模型—传递函数

1、传递函数的定义及性质

（1）传递函数是在零初始条件下，线性定常系统输出量拉氏变换与输入量拉氏变换之比。零初始条件有两方面含义：一是指输入作用是在 $t=0$ 以后才作用于系统的，因此，系统输入量及其各阶导数在 $t\leq 0$ 时刻均为零；二是指输入作用于系统之前，系统是“相对静止”的，即系统输出量及各阶导数在 $t\leq 0$ 时刻的值也为零。

（2）传递函数的推导及其标准形式：

（3）举例：

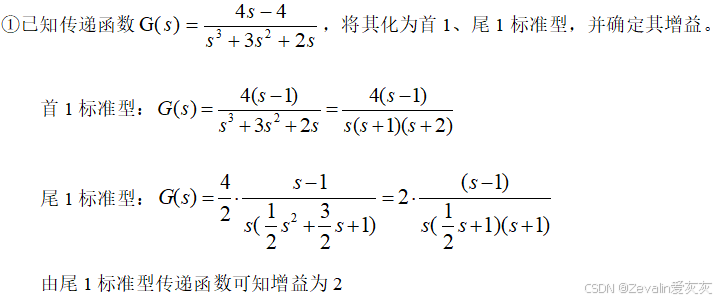
（4）传递函数的性质：

①传递函数是复变量s的有理分式，它具有复变函数的所有性质。因为实际物理系统总是存在惯性的，并且能源功率有限，所以实际系统传递函数的分母阶次n总是大于或等于分子阶次m，即n≥m。

②传递函数只取决于系统或元部件自身的结构和参数，与外作用的形式和大小无关。

③传递函数与微分方程有直接联系，复变量s相当于时域中的微分算子。

④传递函数的拉氏反变换即为系统的脉冲响应。

（5）传递函数的局限性：

①传递函数是在零初始条件下定义的，因此它只反映系统在零状态下的动态特性，不能反映非零初始条件下系统的全部运动规律。

②传递函数通常只适合用于描述单输入-单输出系统。

③传递函数是由拉氏变换定义的，拉氏变换是一种线性变换，因此传递函数只适用于线性定常系统。

2、一些常用控制元件的传递函数

（1）电位器：

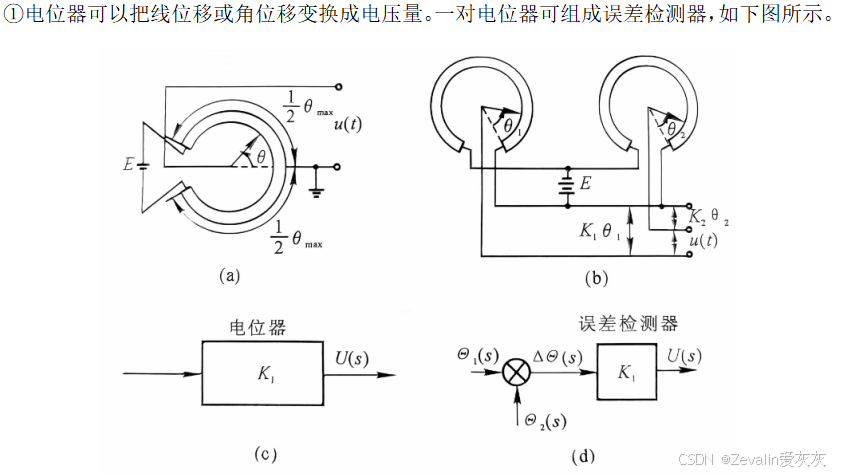
（2）自整角机：

（3）测速发电机：

（4）电枢控制式直流电动机：

（5）两相异步电机：

①两相异步电机由相互垂直配置的两相定子线圈和一个高电阻值的转子组成。定子线圈的一相是激磁绕组，另一相是控制绕组，通常接在功率放大器的输出端，提供幅值可调节的交流控制电压。

②两相异步电动机的转矩-速度特性曲线有负的斜率，且呈非线性，下图所示的是不同控制电压 $u_{a}$ 下实验测取的一组机械特性曲线。考虑到在控制系统中，异步电动机一般工作在零转速附近，作为线性化的一种方法，通常把低速部分的线性段延伸到高速范围，用低速直线近似代替非线性特性，此外，也可应用小偏差线性化方法。