论文笔记 | Rethinking the Inception Architecture for Computer Vision

醉醉的，写完之后竟然被新的文章代替了，只能重新写一遍了～

Authors

Christian Szegedy Vincent Vanhoucke Sergey Ioffe Jonathon Shlens

Abstract

Here we are exploring ways to scale up networks in ways that aim at utilizing the added computation as efficientily as possible by suitably factorized convolutions and aggressive regularization

1 Introduction

googlenet v1 is much harder to adapt to new use-cases while maintaining its efficiency, for example, if it is deemed necessary to increase the capacity o some inception model, if just doubling the number of all filter bank sizes will lead to a 4x increase in both computational cost and number of parameters.

2 General design principles

2.1 Aviod representational bottlenecks, especially early in the network

In general the representation size should gently decrease from the inputs to the outputs before reaching the final representaion used for the task at hand.
Theoretically, information content can not be assessed merely by the dimensionality of the representation as it discards important factors like correlation structure.

2.2 Higher dimensional representations are easier to process locally within a network.

in creasing the activations per tile in a convolutional network allows for more disentangeled features. The resulting networks will train faster.

2.3 Spatial aggregation can be done over lower dimensional embeddings wihout much or any loss in representational power

we hypothesize that the reason for that is the strong correlation between adjacent unit results in much less loss of inforamtion during dimension reduction.
The dimension reduction even promotes faster learning .

2.4 balance the width and depth of the network

width= number of filters per stage
for the reason of computational budget.

3 faxtorizing convolutions with large filter size

In a vision network, it is expected that the outputs of near-by activations are highly correlated. Therefore , we can expect that their activations can be redued before aggregation.

3.1 factorization into smaller convlutions

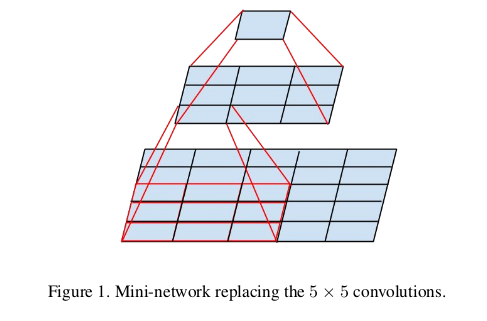
we have found that linear activation was always inferior to using rectified linear units in all stages of the factorization.
we attribute this gain to the enhanced space of variations that the network can learn expecially if we batchnormalize the output activations.

3.2 Spatial Factorization into Asymmetric convolutions

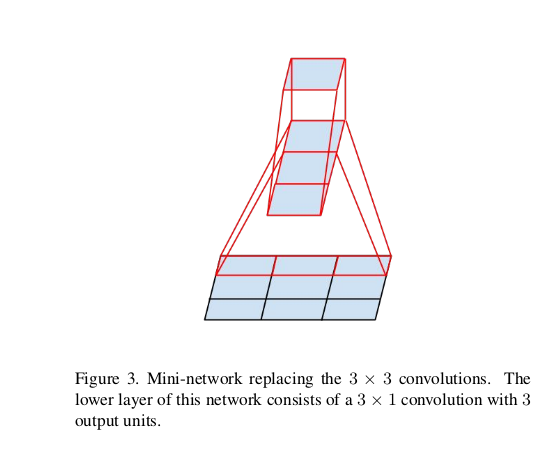
In practice, we have found that employ8ing this factorization des not work well on early layers , but it gives very good results on medium grid-sizes( on mxm feature maps, where m ranges between 12 and 20) on that level, very good results can be achieved by using 1x7 and 7x1

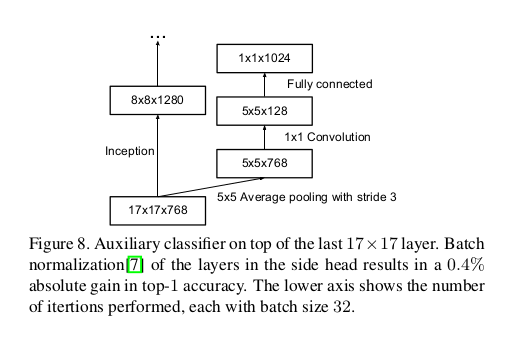
4 uility of auxiliary classifiers

We found that auiliary classifiers did not result in improved convergence early in the training.Near the end of training, the network with the auxiliary branches starts to overtake the accuracy of the network without any auxiliary branch and reaches a slightly higher plateau.
The ramoval of the lower auxiliary branch did not have any adverse effect on the final quality of the network.this means that these branches might not help low level features. but we argue that the auxiliary calssifier act as regularizer.
this is supported by the fact that the main classifier of the network performs better if the side branch is batch normalized or have a dropout layer. This also gives a weak supporting evidence for the conjecture that batch normaolization acts as a regularizer.

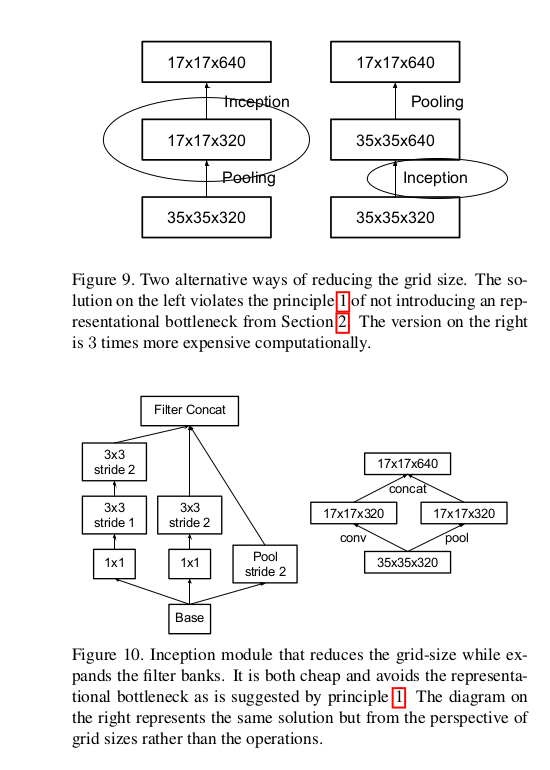
5 efficent grid size reduction

In order to avoid a representation bottleneck, before applying pooling layer the activation dimension of the network filters is expanded.

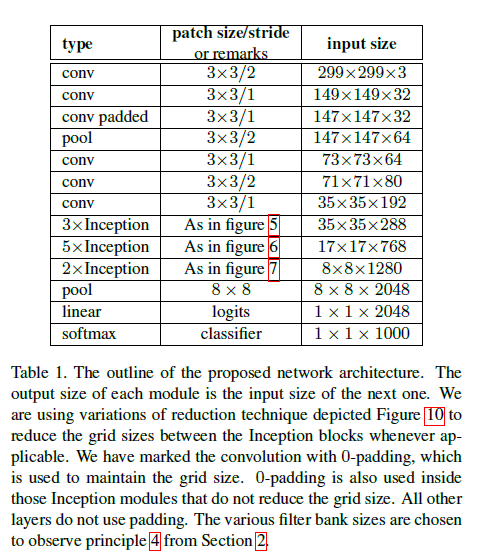
6 Inception v2

42 layer deep

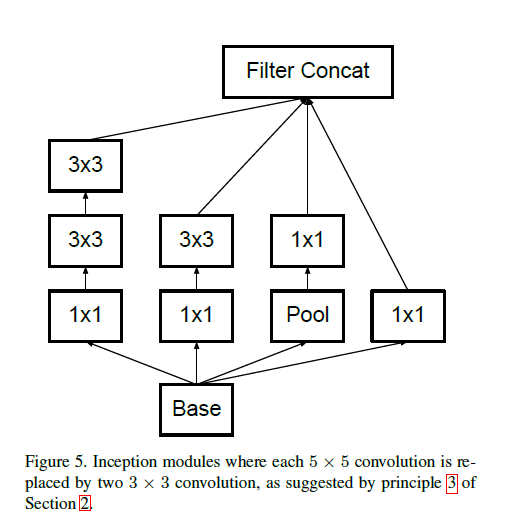
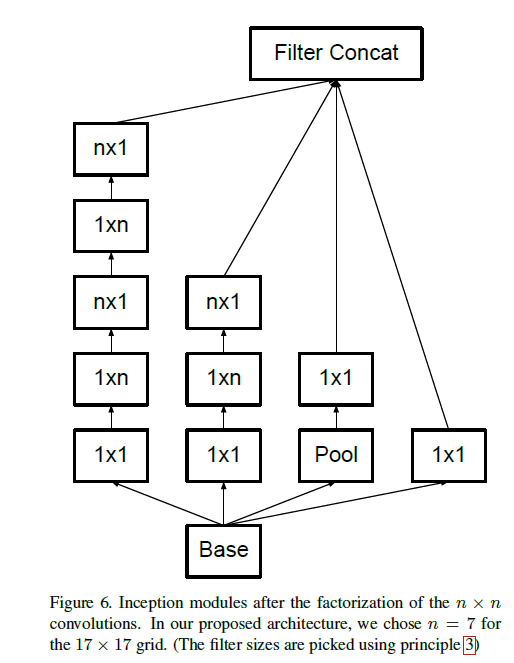
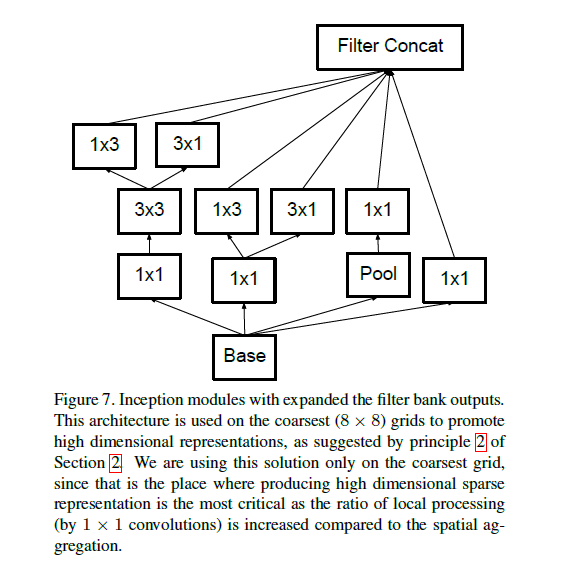
7 model regularization via label smoothing

Consider a distribution over labels u(k), indepandent of training example x and a smoothing parameter$\epsilon$, we replace the label distribution $q(k|x)=\delta_{k,y}$:

$$q'(k|x)=(1-\epsilon)\delta_{k,y}+\epsilon u(k)$$
Cross entropy:

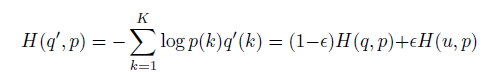
In our imagenet experiments with k=1000 classes, u(k)=1/1000, $\epsilon=0.1$, 0.2% imporvement both for top-1 and top-5

8 training

batch size:32
iteration:100epochs
learning rate:0.045, decayed every two epoch exponential rate of 0.94
momentum 0.9
best models: RMSProp decay of 0.9 $\epsilon=1.0$
gradient clipping

R. Pascanu, T. Mikolov, and Y. Bengio. On the difficulty
of training recurrent neural networks. arXiv preprint
arXiv:1211.5063, 2012.

9 lower resolution input

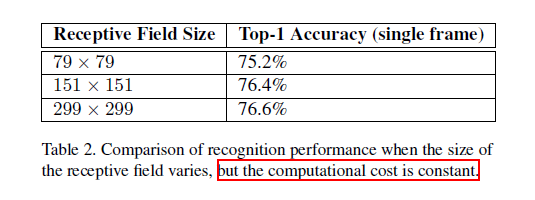
10 v3

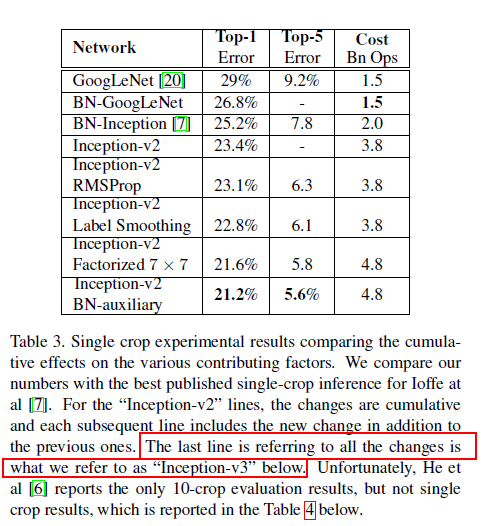
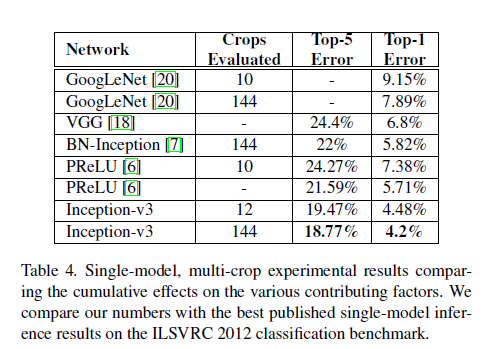
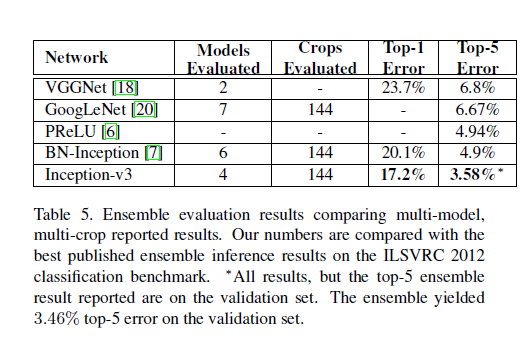
conclusion