这篇文章的主要目的是介绍有效前沿这个理论工具和分析框架。我们由均值方差分析展开,逐步推演到有效前沿。然后,我们又说到有效前沿在投资或者量化中的应用场景,最后我们也总结了有效前沿的一些问题,尤其是敏感性问题。在教程中,特意加入了一些实验代码,可以让大家在阅读的过程中有更好的理解。
有效前沿
说到有效前沿(有些叫效率边界),就要提到马科维茨的投资组合理论了。
首先介绍下它的三大假设:
单一投资期,比如一年
流动性很高,无交易成本
投资者的选择基于最优均值方差
于是,我们可以开始推导有效前沿,在这之前,我们先约定一些数学符号:
- rf:无风险利率
- μ:风险资产预期收益率向量
- f:风险资产预期超额收益率向量,即μ−rfμ−rf
- Σ:风险资产协方差矩阵
- w:风险资产组合权重向量
我们采用三个步骤来得到我们的有效市场前沿,分别是最小方差组合、最优均值方差组合(夏普组合)以及有效前沿。当我们推导完,大家就会发现有效前沿与前两个组合之间存在有趣的关系,最后我们将用python代码的方式来实现并检验我们得到的结果。
在下面我们模拟了三个风险资产,并用python画出了有效前沿曲线。图1还标注了最小方差组合(C组合)、最优夏普组合(Q组合)以及全额等权组合(E组合)。
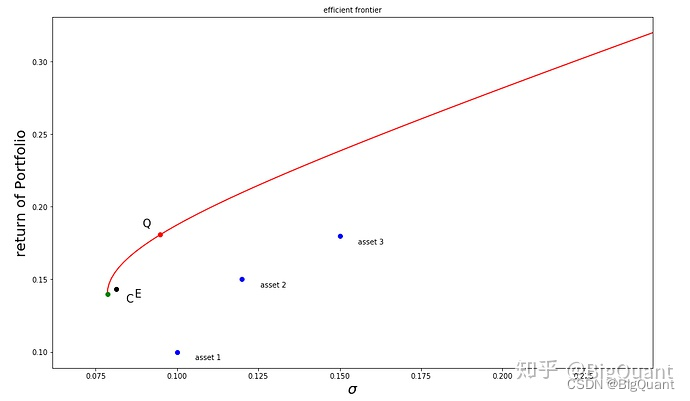
图1
有效前沿的应用
有效前沿曲线告诉我们,在全额投资的条件下,所有基于风险厌恶型的投资者都应该选择有效前沿曲线上投资组合,它们是均值方差最优的。那么这个理论工具怎么能够帮助我们做投资决策呢?
首先我们应用这个理论工具的基本条件是要有市场中所有风险资产或者可投资风险资产的预期收益率和预期协方差矩阵





 本文探讨了有效前沿在投资组合优化中的应用,从均值方差分析开始,介绍了有效前沿的敏感性问题,并通过Python代码展示实际策略实验。文章指出,尽管有效前沿存在敏感性,但仍是风险厌恶投资者的重要工具。
本文探讨了有效前沿在投资组合优化中的应用,从均值方差分析开始,介绍了有效前沿的敏感性问题,并通过Python代码展示实际策略实验。文章指出,尽管有效前沿存在敏感性,但仍是风险厌恶投资者的重要工具。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 991
991

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








