▲基于MPC的非线性摆锤系统轨迹跟踪控制matlab仿真

最新推荐文章于 2025-04-30 14:27:27 发布

fpga和matlab

最新推荐文章于 2025-04-30 14:27:27 发布

阅读量721

点赞数 25

分类专栏： FPGA/MATLAB精品资源专栏文章标签： matlab 算法 MPC 非线性摆锤系统轨迹跟踪控制

本文链接：https://blog.csdn.net/ccsss22/article/details/143611026

版权

FPGA/MATLAB精品资源专栏专栏收录该内容

63 篇文章

订阅专栏

非线性摆锤系统是一个典型的非线性动力学系统，在物理学、工程学等领域有着广泛的应用。对非线性摆锤系统进行精确的轨迹跟踪控制是一个具有挑战性的问题。模型预测控制（Model Predictive Control，MPC）是一种先进的控制方法，它能够有效地处理非线性系统的约束和优化问题，因此在非线性摆锤系统的轨迹跟踪控制中具有很大的潜力。

1.非线性摆锤系统的数学模型

非线性摆锤系统通常由一个摆锤和一个支点组成，摆锤在重力作用下围绕支点摆动。其动力学方程可以用拉格朗日方程或牛顿力学方法推导得到。考虑一个单摆系统，摆锤的质量为m，摆长为l，摆锤与竖直方向的夹角为theta。根据牛顿力学，摆锤的动力学方程可以表示为：

2.模型预测控制的基本原理

模型预测控制是一种基于模型的优化控制方法，它通过在每个采样时刻预测系统未来的行为，并根据预测结果优化控制输入，以实现对系统的最优控制。

在 MPC 中，首先需要建立一个预测模型，用于预测系统未来的状态。对于非线性摆锤系统，可以使用近似线性化的方法或者非线性模型预测的方法来建立预测模型。

MPC 通过优化一个目标函数来确定最优的控制输入。对于非线性摆锤系统的轨迹跟踪控制，目标函数通常包括跟踪误差和控制输入的代价。

在 MPC 中，还需要考虑系统的约束条件，以确保控制输入的可行性和系统的安全性。对于非线性摆锤系统，可能的约束条件包括：

在每个采样时刻，MPC 根据当前的系统状态和预测模型，求解优化问题，得到最优的控制输入序列。

3.MATLAB程序

..........17..............................................................
 % 获取整个预测时域的参考轨迹，将结果赋给 rr
    rr =  func_ref(rr,ref,t,np,nx);
    
    
    % 计算系统输出，将结果赋给 y 的第 t 列
    y(:,t) = C*x+D*ui;
    
    
    % 使用四阶龙格-库塔积分器模拟前进一步，更新状态向量 x 和状态导数向量 dx
    [x, dx] = func_RK(x,ui,Ts,model);
    
    
    % 计算当前状态下系统的线性化和离散化状态矩阵 A 和输入矩阵 B
    [A, B] = func_linearizePendulumODE(x, Para, Ts);
    
    
    % 计算预测时域上的阶段约束矩阵 Dt、Et 和向量 bt
    [Dt,Et,bt]=func_genStageConstraints(A,B,Dcon,Pmin,Pmax,umin,umax);
    
    
    % 计算预测时域上的轨迹约束矩阵 DD、EE 和向量 bb
    [DD,EE,bb]=func_genTrajectoryConstraints(Dt,Et,bt,np);
    
    
    % 计算预测时域上的预测矩阵 Gamma 和 Phi
    [Gamma,Phi] = func_genPrediction(A,B,np);
    
    
    % 计算预测时域上的二次规划约束矩阵 F、J 和 L
    [F,J,L]=func_genConstraintMatrices(DD,EE,Gamma,Phi,np);
    
    
    % 计算二次规划代价矩阵 H 和 G
    [H,G] = func_genCostMatrices(Gamma,Phi,Q,R,P,np);
    
    
    % 对 H 进行下三角分解，并计算其逆，用于 mpcqpsolver 的准备工作
    H = chol(H,'lower');
    H=(H'\eye(size(H)))';
    
    
    % 设置约束在此时为不活动状态，初始化活动不等式向量 iA
    iA = false(size(bb));
    
    
    % 生成最优输入步长，调用 func_MPController 函数，更新输入向量 u 和活动不等式向量 iA
    [u,~,iA] = func_MPController(H,G,F,bb,J,L,x,rr(1:nx),1,iA);
    % 将 u 的第一个元素赋给 ui，作为系统的输入
    ui = u(1:nu);   
    
    uh(:,t) = ui;% 将 ui 存储到输入结果向量 uh 的第 t 列

4.仿真结果

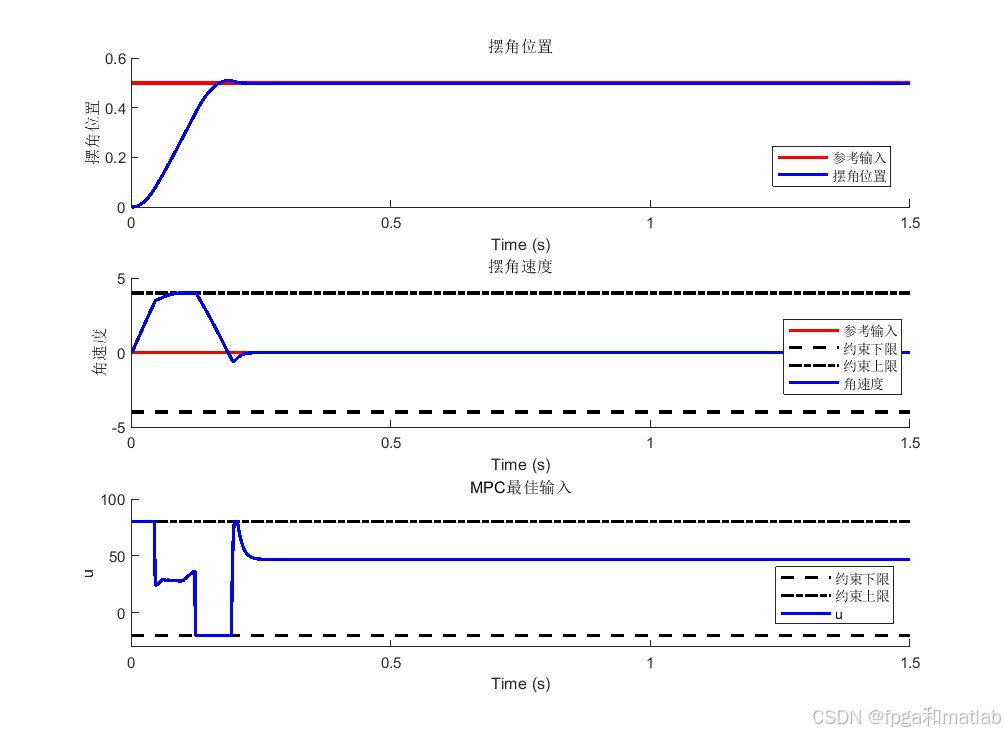
基于 MPC 的非线性摆锤系统轨迹跟踪控制是一种有效的控制方法，它能够处理非线性系统的约束和优化问题，实现对非线性摆锤系统的精确轨迹跟踪。在实际应用中，还需要考虑系统的不确定性、噪声干扰等因素，进一步提高算法的鲁棒性和适应性。此外，还可以结合其他先进的控制方法，如自适应控制、鲁棒控制等，以提高系统的性能。