目录
1.QPSK调制原理
QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。在19世纪80年代初期,人们选用恒定包络数字调制。这类数字调制技术的优点是已调信号具有相对窄的功率谱和对放大设备没有线性要求,不足之处是其频谱利用率低于线性调制技术。19世纪80年代中期以后,四相绝对移相键控(QPSK)技术以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接入、移动通信及有线电视系统之中。通过完成设计内容, 学习QPSK调制解调的基本原理,同时也要复习通信系统的主要组成部分,了解调制解调方式中最基础的方法。了解QPSK的实现方法及数学原理。并对“通信”这个概念有个整体的理解,学习数字调制中误码率测试的标准及计算方法。同时还要复习随机信号中时域用自相关函数,频域用功率谱密度来描述平稳随机过程的特性等基础知识,来理解高斯信道中噪声的表示方法,以便在编程中使用。
理解QPSK调制解调的基本原理,并使用MATLAB编程实现QPSK信号在高斯信道和瑞利衰落信道下传输,以及该方式的误码率测试。复习MATLAB编程的基础知识和编程的常用算法以及使用MATLAB仿真系统的注意事项,并锻炼自己的编程能力,通过编程完成QPSK调制解调系统的仿真,以及误码率测试,并得出响应波形。在完成要求任务的条件下,尝试优化程序。通过本次实验,除了培养了自主动手学到了知识之外,还可以将次研究作为一种推广,让自己来深入一层的了解QPSK以至其他调制方式的原理和实现方法。可以方便自己进行测试和对比。
正交相移键控(Quadrature Phase Shift Keying,QPSK)是一种数字调制方式。它分为绝对相移和相对相移两种。由于绝对相移方式存在相位模糊问题,所以在实际中主要采用相对移相方式DQPSK。QPSK是一种四进制相位调制,具有良好的抗噪特性和频带利用率,广泛应用 于卫星链路、数字集群等通信业务。
OQPSK是在QPSK基础上发展起来的一种恒包络数字调制技术。恒包络技术是指已调波的包络保持为恒定,它与多进制调制是从不同的两个角度来考虑调制技术的。恒包络技术所产生的已调波经过发送带限后,当通过非线性部件时,只产生很小的频谱扩展。这种形式的已调波具有两个主要特点,其一是包络恒定或起伏很小;其二是已调波频谱具有高频快速滚降特性,或者说已调波旁瓣很小,甚至几乎没有旁瓣。采用这种技术已实现了多种调制方式。OQPSK信号,它的频带利用率较高,理论值达1b/s/Hz。在QPSK中,当码组0011或0110时,产生180°的载波相位跳变。这种相位跳变引起包络起伏,当通过非线性部件后,使已经滤除的带外分量又被恢复出来,导致频谱扩展,增加对相邻波道的干扰。为了消除180°的相位跳变,在QPSK基础上提出了OQPSK。
QPSK是一种利用载波的四种不同相位来表示数字信息的调制方式。在QPSK中,每个码元周期内载波的相位有四种可能取值,通常分别为 0、π/2、π、3π/2,或者可以表示为 ±π/4、±3π/4。由于每种相位状态可以代表2个比特的信息,因此QPSK可以在相同的带宽下传输比 BPSK 更多的数据,从而提高了频谱利用率。

调制的结构框图如下图所示:

2.QPSK解调原理
QPSK解调原理:

四相相移调制是利用载波的四种不同相位差来表征输入的数字信息,是四进制移相键控。QPSK是在M=4时的调相技术,它规定了四种载波相位,分别为45°,135°,225°,315°,调制器输入的数据是二进制数字序列,为了能和四进制的载波相位配合起来,则需要把二进制数据变换为四进制数据,这就是说需要把二进制数字序列中每两个比特分成一组,共有四种组合,即00,01,10,11,其中每一组称为双比特码元。每一个双比特码元是由两位二进制信息比特组成,它们分别代表四进制四个符号中的一个符号。
在数字信号的调制方式中QPSK四相移键控是目前最常用的一种卫星数字信号调制方式,它具有较高的频谱利用率、较强的抗干扰性、在电路上实现也较为简单。目前已经广泛应用于无线通信中,成为现代通信中一种十分重要的调制解调方式。

QPSK的调制解调算法相对简单,易于在数字信号处理芯片或专用集成电路中实现,与一些更复杂的调制方式如16QAM、64QAM等相比,其实现成本较低,对硬件的要求相对不高,因此在许多通信系统中得到了广泛应用。
3.LDPC编译码
LDPC码作为一种前向纠错码,具有卓越的性能,其纠错能力能够接近香农极限 。这意味着在理论上,LDPC码能够在极低的信噪比条件下实现可靠的数据传输,大大提高了通信系统的效率和可靠性。在深空通信中,由于信号传输距离极远,信号强度会随着距离的增加而急剧衰减,导致信噪比极低。LDPC码的应用能够在这种恶劣的信道条件下,有效地纠正传输过程中产生的错误,确保数据的准确传输。
LDPC码的校验矩阵具有稀疏性,这是其区别于其他编码的重要特性之一。稀疏校验矩阵意味着矩阵中大部分元素为零,只有少数元素为非零值。这种稀疏性使得 LDPC 码在编码和解码过程中具有较低的复杂度,因为在矩阵运算中,与零元素的运算可以省略,从而减少了计算量和存储需求。与一些传统的编码方式相比,如卷积码,其校验矩阵相对密集,在处理长码长时,计算复杂度会显著增加,而LDPC码的稀疏校验矩阵则能够有效地避免这一问题,使得在处理长码长数据时仍能保持较低的计算复杂度。
完整链路流程为:
1.信息比特 u → LDPC编码 → 码字c
2.BPSK调制 → 信道传输 → 接收信号y
3.LDPC译码 → u^
在发送端,原始信息比特先经过LDPC编码,增加冗余信息以提高纠错能力;然后进行BPSK 调制,将数字信号转换为适合信道传输的模拟信号;经过信道传输后,在接收端先进行BPSK解调,得到解调后的信号;再进行LDPC译码,恢复出原始信息比特。
4.MATLAB程序
52.................................................................
% 调制
CARRIERI=[];
QPSKI=[];
CARRIERQ=[];
QPSKQ=[];
for i=1:Num/2
tmps1(i) = 2*bitsI(i)-1;
tmps2(i) = 2*bitsQ(i)-1;
QPSKI=[QPSKI,tmps1(i)*sa1];
QPSKQ=[QPSKQ,tmps2(i)*sa2];
CARRIERI=[CARRIERI,sa1];
CARRIERQ=[CARRIERQ,sa2];
end
%相加
RQPSK = QPSKI+QPSKQ;
%%
RQPSK = awgn(RQPSK,SNR(ij2),'measured');
Ydemod1 = RQPSK.*CARRIERI;
Ydemod2 = RQPSK.*CARRIERQ;
w = hamming(53);
yfilter1 = filter(w,1,Ydemod1);
yfilter2 = filter(w,1,Ydemod2);
%判决
yod1 = [];
yod2 = [];
for i=1:Num/2
tmps1 = yfilter1(4*Nsamp*(i-1)+Nsamp:4*Nsamp*i-Nsamp);
yod1 = [yod1;mean(tmps1)];
tmps2 = yfilter2(4*Nsamp*(i-1)+Nsamp:4*Nsamp*i-Nsamp);
yod2 = [yod2;mean(tmps2)];
end
yod=zeros(1,Num);
yod(1:2:end)=yod1;
yod(2:2:end)=yod2;
yod = yod/max(yod);
sigma = sqrt(1./(2*10^(SNR(ij2)/10)*R));
z_hat = func_Dec(yod,sigma,H,max_iter);
x_hat = [z_hat(size(G,2)+1-size(G,1):size(G,2))]';
err(ij2,kk) = 1-length(find(bits0(1:end)==x_hat(1:end)))/length(x_hat);
end
end
figure;
semilogy(SNR,mean(err,2),'-b^',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.2,0.9,0.5]);
grid on
xlabel('SNR');
ylabel('error');
title('QPSK调制解调误码率曲线');
.......................................................................5.仿真结果
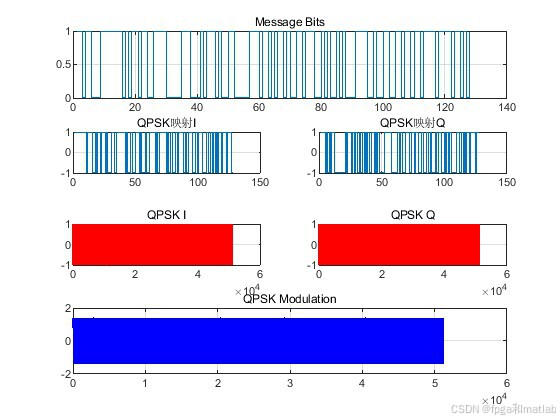
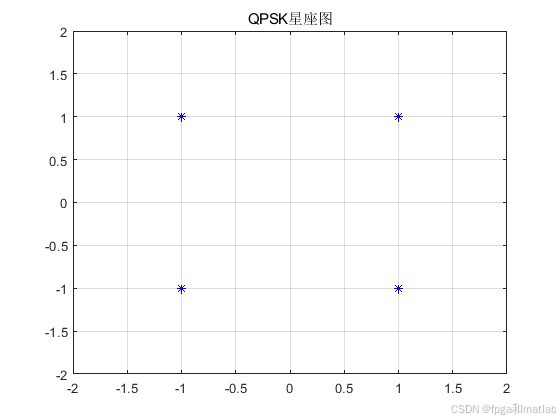
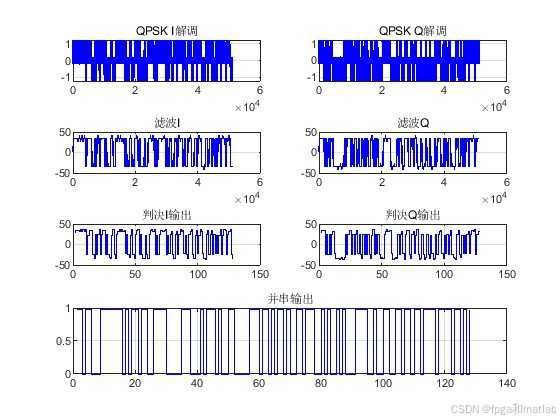
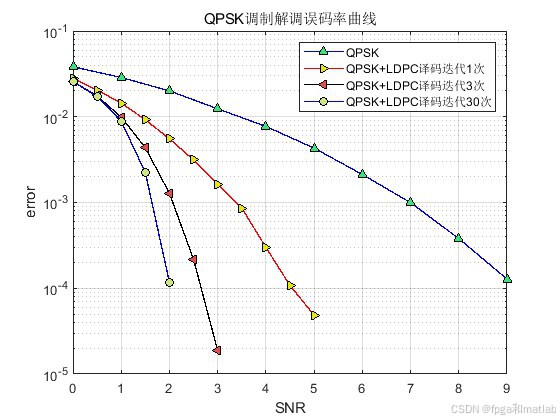
6.完整程序下载
完整可运行代码,博主已上传至CSDN,使用版本为matlab2022a:
(本程序包含程序操作步骤视频)
基于QPSK调制解调+LDPC编译码通信链路matlab误码率仿真【包括程序,中文注释,程序操作视频】资源-CSDN文库

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










