pytorh——Fully-connected

最新推荐文章于 2024-09-03 18:10:16 发布

Hali_Botebie

最新推荐文章于 2024-09-03 18:10:16 发布

阅读量2.7k

点赞数

CC 4.0 BY-SA版权

分类专栏：训练心得与Pytorch实践

原文链接：baidu.com

训练心得与Pytorch实践专栏收录该内容

40 篇文章

订阅专栏

首先我们明白全连接层的组成如下
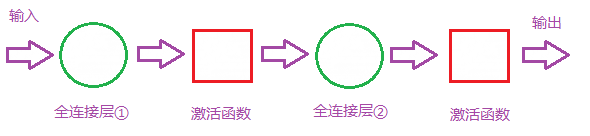在这里插入图片描述那么全连接层对模型影响参数就是三个：

全接解层的总层数（长度）
单个全连接层的神经元数（宽度）
激活函数

全连接层（fully connected layers, FC)在整个卷积神经网络中起到”分类器“的作用。如果说卷积层，池化层和激活函数层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的”分布式特征表示“映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现；

对前层是全连接的全连接层可以转化为卷积核为11的卷积，而前层是卷积层的全连接层可以转化为卷积核为hw的全局卷积，h和w分别为前层卷积结果的高和宽。

全连接的核心操作就是矩阵向量乘积y=Wx

本质就是由一个特征空间线性变换到另一个特征空间。目标空间中的任一维——也就是隐层的一个cell——都认为会受到源空间的每一维的影响。不考虑严谨，可以说，目标向量是源向量的加权和。

在CNN中，全连接常出现在最后几层，用于对于前面设计的特征做加权和，比如mnist，前面的卷积和池化相当于做特征工程，后面的全连接相当于做特征加权。（卷积相当于全连接的有意弱化，按照局部视野的启发，把局部之外的弱影响直接抹为0影响，还做了一点强制，不同的局部所使用的参数居然一致。弱化使参数变少，节省计算量，又专攻局部不贪多求全，强制进一步减少参数。在RNN中，全连接用来把embedding空间拉到隐层空间，把隐层空间转回label空间等。

全连接层的作用主要就是实现分类（Classification）
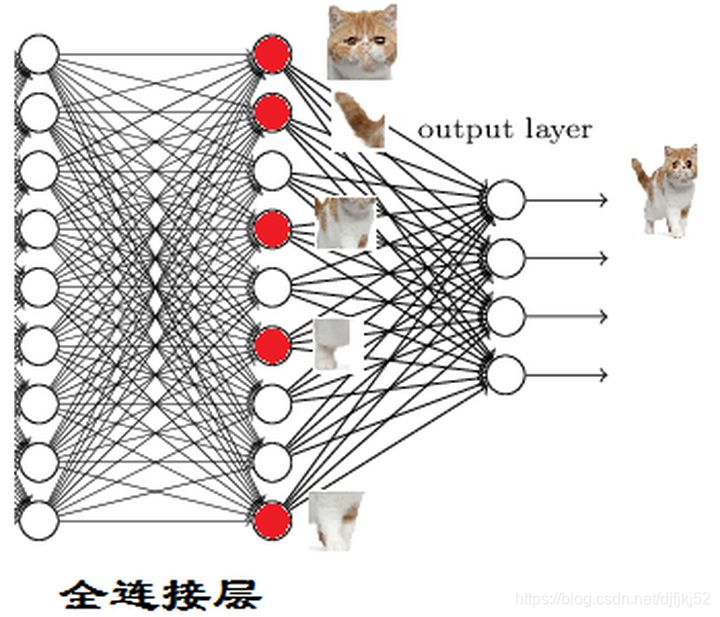
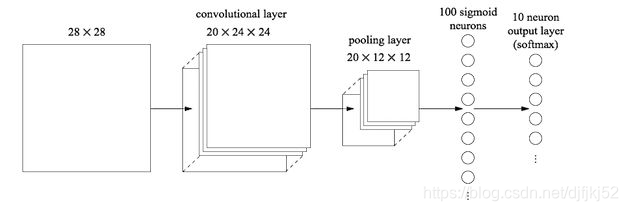
在这里插入图片描述
还是就这张图而言，经过若干卷积层和池化层之后，会输出20个1212的矩阵（是矩阵，不是图片，虽然可以可视化，但一般已经没有人能理解的部分在了），这代表用了20个神经元，每个神经元都对这张图进行了一次次卷积，并且每个神经元最后输出的1212的矩阵都代表了这个神经元对该图片的一个特征的理解接下来就到了全连接层，输出一个1100的矩阵，全连接层是100个1212的卷积核，每个1212的卷积核都对这20个1212的图片进行卷积，得到20个数，将这20个数求和得到矩阵中的一个数，一共100个卷积核，所以一共是100个数，而这100个数，代表着用于分类的最基本特征，比如有耳朵，有尾巴，有眼睛…（只是比如）最后再经过一个分类器（也是一个全连接层？），假设要分猫，狗，兔子，那么对这些特征再进行一次计算（降维），将其中的某几个特征求和，输出最后的1*3的矩阵，每个数代表了各个类别的概率（或得分）

torch.nn.Linear()函数的理解

class torch.nn.Linear(in_features, out_features, bias=True)

对输入数据做线性变换：y=Ax+b

参数：

in_features - 每个输入样本的大小
out_features - 每个输出样本的大小
bias - 若设置为False，这层不会学习偏置。默认值：True

形状：

输入: (N,in_features)

输出： (N,out_features)

变量：
weight -形状为(out_features x in_features)的模块中可学习的权值
bias -形状为(out_features)的模块中可学习的偏置

torch.nn.Linear类用于定义模型的线性层，即完成前面提到的不同的层之间的线性变换。torch.nn.Linear类接收的参数有三个，分别是输入特征数、输出特征数和是否使用偏置，设置是否使用偏置的参数是一个布尔值，默认为True，即使用偏置。

在实际使用的过程中，我们只需将输入的特征数和输出的特征数传递给torch.nn.Linear类，就会自动生成对应维度的权重参数和偏置，对于生成的权重参数和偏置，我们的模型默认使用了一种比之前的简单随机方式更好的参数初始化方法。

根据我们搭建模型的输入、输出和层次结构需求，它的输入是在一个批次中包含100个特征数为1000的数据，最后得到100个特征数为10的输出数据，中间需要经过两次线性变换，所以要使用两个线性层，两个线性层的代码分别是torch.nn.Linear(input_data,hidden_layer)和torch.nn.Linear(hidden_layer, output_data)。可看到，其代替了之前使用矩阵乘法方式的实现，代码更精炼、简洁。

import torch

x = torch.randn(128, 20)  # 输入的维度是（128，20）
m = torch.nn.Linear(20, 30)  # 20,30是指维度
output = m(x)
print('m.weight.shape:\n ', m.weight.shape)
print('m.bias.shape:\n', m.bias.shape)
print('output.shape:\n', output.shape)

# ans = torch.mm(input,torch.t(m.weight))+m.bias 等价于下面的
ans = torch.mm(x, m.weight.t()) + m.bias   
print('ans.shape:\n', ans.shape)

print(torch.equal(ans, output))

因为线性变换的公式是：

$y=xA^T+b$
先生成一个（30，20）的weight，实际运算中再转置，这样就能和x做矩阵乘法了

本人发现在卷积层与第一个全连接层的全连接层的input_features不知道该写多少

后来发现，写完卷积层后可以根据模拟神经网络的前向传播得出这个。

全连接层的input_features是多少。首先来看一下这个简单的网络。这个卷积的Sequential本人就不再啰嗦了，现在看nn.Linear(？？？, 4096)这个全连接层的第一个参数该为多少呢？请看下文详解。

class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()

        self.conv = nn.Sequential(
            nn.Conv2d(3, 96, kernel_size=11, stride=4),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),

            nn.Conv2d(96, 256, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),

            nn.Conv2d(256, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2)
        )

        self.fc = nn.Sequential(
            nn.Linear(？？？, 4096)
            ......
            ......
        )

首先，我们先把forward写一下：

    def forward(self, x):
        x = self.layer5(self.layer4(self.layer3(self.layer2(self.layer1(x)))))
        print x.size()# 得到特征图，用view把卷积输出的特征图弄成二维
        x = x.view(-1, 6*6*256)# 用view把卷积输出的特征图弄成二维
        x = self.layer8(self.layer7(self.layer6(x)))
        
        return x

其他解决方法是，

(1)传入输入数据的大小，然后使用公式(height + kernel[0] - 2) // stride[0] + 1计算height，(width + kernel[1] - 2) // stride[1] + 1计算卷积后大小并传递到下层依次计算
(2) view把卷积输出的特征图弄成二维的才行

分析输入网络的形状

输入该网络层的形状(N, *, in_features)，其中N为批量处理过成中每批数据的数量，*表示，单个样本数据中间可以包含很多维度，但是单个数据的最后一个维度的形状一定是in_features.

经过该网络输出的形状为(N, *, out_features),其中计算过程为：

$N, *, in\_{features}] * {[out\_{features }, in\_{features}]}^T = [N, *, out\_{features}]$

用法示例：

import torch as t
from torch import nn

# in_features由输入张量的形状决定，out_features则决定了输出张量的形状 
connected_layer = nn.Linear(in_features = 64*64*3, out_features = 1)

# 假定输入的图像形状为[64,64,3]
input = t.randn(1,64,64,3)

# 将四维张量转换为二维张量之后，才能作为全连接层的输入
input = input.view(1,64*64*3)
print(input.shape)
output = connected_layer(input) # 调用全连接层
print(output.shape)

input shape is %s torch.Size([1, 12288])
output shape is %s torch.Size([1, 1])

2021年5月18补充

全连接层（Fully Connected Layer）的输出张量（图像）的大小
全连接层输出向量长度等于神经元的数量。

全连接层在整个卷积神经网络中起到“分类器”的作用。
如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
在实际使用中，全连接层可由卷积操作实现：
- 对前层是全连接的全连接层可以转化为卷积核为 $1 * 1$ 的卷积；
- 前层是卷积层的全连接层可以转化为卷积核为 $h * w$ 的全局卷积，h和w分别为前层卷积结果的高和宽。
目前由于全连接层参数冗余（仅全连接层参数就可占整个网络参数80%左右），近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代FC来融合学到的深度特征，最后仍用softmax等损失函数作为网络目标函数来指导学习过程。
- 需要指出的是，用GAP替代FC的网络通常有较好的预测性能。
- 思想就是：用 feature map 直接表示属于某个类的 confidence map，比如有10个类，就在最后输出10个 feature map，每个feature map中的值加起来求平均值，然后把得到的这些平均值直接作为属于某个类别的 confidence value，再输入softmax中分类，更重要的是实验效果并不比用 FC 差。

对 1 * 1 卷积可以减少参数进行举例：

如果:
input feature map是 $7 * 7 * 512$
output feature map是 $1 * 1 * 4096$

如果使用全连接，那么需要的权值参数数目(忽略偏置参数，下同)为 $7 * 7 * 512 * 4096$
如果使用 $7 * 7$ 卷积核，需要的权值参数数目为 $7 * 7 * 512 * 4096$
如果使用 $1 * 1$ 卷积核，且权值共享，需要的权值参数数目为11512*4096
- 但得到的output feature map为774096
- 需要再做一个global average pooling才能变为114096
- 此时确实可以减少权植参数数目。

https://blog.csdn.net/qq_34807908/article/details/81736336

参考

https://www.zhihu.com/question/41037974
https://blog.csdn.net/weixin_38145317/article/details/111270687
https://blog.csdn.net/zw__chen/article/details/82839061