模糊控制理论总结

注意，下面集合都是指的模糊集合

一、模糊集合基础知识

（一）模糊集合

1.模糊集合：

论域U到[0,1]区间上的任一映射,都确定一个模糊集合F。与普通集合不同，模糊集合一般用来表示一些模糊的概念，比如速度是“大”，“中”，“小”，温度“高”、“中”、“低”等

2.名词解释：

        U表示模糊集合的论域，u表示论域U中的元素，表示u属于模糊集合F的程度，即隶属度，其范围是[0,1]。

3.模糊集合表示方法

        1）zadeh法：（元素个数有限时采用）

        

        2）序偶法：（元素个数有限时采用）

        

        3）隶属函数描述法：

        

4.模糊集合的运算

        1）并运算：两个模糊集合的并集，其隶属函数为两个模糊集隶属度取大

        

        2）交运算：两个模糊集合的交集，其隶属度函数为两个模糊集隶属度取小

        

        3）补运算：

        

例题介绍：

        模糊论域为U，A表示“大”、B表示“小”为定义在模糊论域上的模糊集合，具体表示如下图：

        

        则相应的计算如下：

        

（二）模糊关系定义

        引入：关系指得是不同集合的元素间的关联程度。

        普通集合的关联：“有关系”——1，“无关系”——0

        设X，Y是两个非空集合，X×Y的一个子集R称为X到Y的一个普通关系；当(x，y)∈R时，称X，Y有关系R；当(x，y)不属于R时，称(x，y)没有关系R。

        模糊集合间的关联：“多大程度上是”，“多大程度上否”来定义     

        1.模糊关系矩阵R

          若U、V是两个非空模糊集，则其直积UxV中的一个模糊子集R称为从U到V的模糊关系。                

         例如，用模糊关系R来描述父母与子女的相像关系

        

        模糊关系R中对应的各隶属度参数含义分别为：

        

        即模糊关系R表示两个非空模糊集{父、母}与{子、女}长相“相像”的关系。

        2.笛卡尔乘积（直积）：

        若A1,A2,...,An分别为论域U1，U2,...,Un中的模糊集合，则这些集合的直积是乘积空间U1XU2X...XUn中的一个模糊集合。其隶属函数为：

        

        3.两个模糊关系R和S的关系运算：

        1）交运算——直接对应位置取小

        2）并运算——直接对应位置取大

        3）模糊关系的合成（最重要）

        

        其中合成运算的运算规则为：

                

       已知：1.模糊集合X,Y的模糊关系R，2.模糊集合Y，Z的模糊关系S

       就可以通过R和S的合成计算出模糊集合X和模糊集合Z的模糊关系C！！！

        4.模糊变换

        设A、B分别为X,Y上的模糊集，且满足关系,就称B为A的像，A是B的原像，R是X到Y上的一个模糊变换。

        对应的计算采用上述的合成运算的法则计算即可。

例题：

        已知论域，输入A是论域X上的模糊集，R是X到Y上的一个模糊变换，试通过模糊变换R求A的像B。

        计算时，先取小后取大

        

二、模糊控制相关知识

（一）语言变量

          模糊控制系统一般用误差e和误差变化率ec作为输入语言变量。

          其语言值集合定义为{“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”}

         每个语言值（如“负大”）对应一个在论域E、EC上定义的模糊数。通过这个模糊数，可以将模糊概念与精确数值练习起来。

        例如：温度T作为语言变量，则其词集可以为{超高、较高、中等、较低、超低}，其中每个模糊语言如“超高”、“较高”等都是定义在论域U上的一个模糊集合。

（二）语言规则中蕴含的模糊关系

        1.如果.....那么.....

        假设u，v是定义在论域U、V的两个语言变量

        语言控制规则：  “如果u是A，v是B”        对应模糊关系R为

        

        其中，为AxB的笛卡尔乘积（）隶属度计算法则。

        最终，R的运算法则为：

        

        2.如果...那么....否则....

        语言控制规则：  “如果u是A，则v是B，否则v是C”        对应模糊关系S为

        

        最终，S的运算法则为：

        

（三）对应到控制器的规则

        规则：如果误差e是小，那么控制量u是大。

        则对应模糊关系的隶属函数为：

        

        例题：定义两个语言变量“误差e”和“控制量u”。两者的论域是E=U={1，2，3，4，5}；

定义在论域上的语言值为{大、小、较小}；定义各语言指的隶属函数为：

        

        1）计算“如果误差e是小，则控制量u是大”蕴含的模糊关系R1

        

（四）模糊推理

       1. 模糊近似推理:（前向推理）

        输入：e为A'（某一语言值，如“正大”） 

        规则：如果e为A，则u为B；

        结论：u为

        其中模糊关系矩阵可以采用Zadeh推理，或者Mamdani推理。采用Mamdani推理是直接用直积表示模糊关系。即：    ，则其隶属度计算为

        2.单输入模糊推理

        设输入语言变量误差e，控制量u之间的模糊关系为R，当e取模糊值A'时，与之相对应的控制量u的取值B'可以通过模糊推理得出，即 。        

        R的获取有两种方法，一种是zadeh法，第二种是mamdani推理方法，分别对应两种推理结果

       1） zadeh法：

        

       2） mamdani推理：（更简单实用）

        

        

        其中叫做A*与A的适配度。表示A*和A的交集的高度；根据Mamdani推理方法，结论可以看作是用α对B进行切割，又叫做削顶法。

        3.多输入模糊推理

        输入语言变量：误差e和误差变化率ec

        输出语言变量：控制量u

        则模糊关系为：

        模糊推理，已知E*和EC*，推理U*:

（五）模糊判决

把模糊推理所得到的模糊输出（模糊集合或者隶属函数），进行计算得到一个精确的控制量（确定的值）。

1.重心法

取模糊隶属函数曲线与横坐标轴围成面积的重心作为代表点。

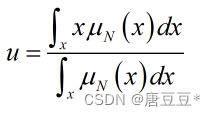
2.最大隶属度法

只要在推理结论的模糊集合中取隶属度最大的那个元素作为输出量即可。如果最大隶属度对应多个元素，则取平均值。

三、模糊控制系统

 （一）模糊控制系统工作过程                              

        

模糊控制器实现过程如下：

控制器实时检测系统的误差e*和ec*——》通过量化因子，将其转化为模糊控制器的精确输入E*和EC*——》将E*和EC*进行模糊化处理，得到模糊输入A*和B*——》结合模糊关系，通过模糊推理得到模糊控制器的输出C*——》对模糊输出C*进行清晰化处理，得到控制器的精确输出量U*——》利用比例因子，将其转化为控制器的实际控制量u*

1.模糊化接口

模糊化就是通过在控制器的输入、输出论语上定义语言变量，将精确的输入、输出值转化为模糊的语言值。

1）.语言变量确定：

a.输入语言变量：误差E，误差变化率EC             输出语言变量：控制量U

b.语言值设计：{“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”}

c.隶属函数设计一般有:

        1）正态分布型

        隶属函数公式           隶属函数图像： 

        2）三角形

        隶属函数公式：

2）语言变量论域设计

将论域定义为有限整数的离散论域：

E：{-m,-m+1,...,-1,0,1,...,m-1,m}              EC:{-n,-n+1,...,-1,0,1,...,n-1,n}

U:{-l,-l+1,...,-1,0,1,...,l-1,l}

3）实现连续论域到有限整数离散论域的转换：

 （1）确定输入量化因子和输出比例因子，用于实现模糊化与解模糊

        量化因子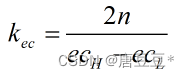：，其中精确输入e的范围是[eH,eL],精确输入ec的范围是[ecH,ecL]，用这个量化因子可以将精确输入转化为模糊输入

        比例因子：

   （2）确定输入量化因子后，则可以将精确输入e和ec转化成模糊输入E和EC

             

   （3）根据模糊输入E和EC得到相应的模糊集合A'，B'

        例如：若误差论域为[-6,-4,-2,0,2,4,6]，当计算出E=-5时，对应三角形隶属函数有。同样，可以获得相应的模糊集合B'。

2.模糊推理(mamdani)

根据7*7=49条控制规则，得到整个规则库的模糊关系R总，即为49条控制规则求并，单条控制规则的模糊关系Ri的求法，前面二、（三）中已经实现，只需要分别求出后再求并即可。

得到整个的模糊关系R总后，只需要利用模糊推理就可以求出模糊输出C':

3.模糊判决接口(重心法)

采用重心法进行模糊判决计算出相应的控制输出：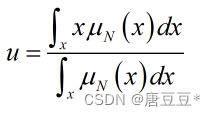

4.实际控制量的转化：

（二）模糊控制系统的设计

步骤：

1.确定模糊控制器的输入变量和输出变量、相应的论域和量化因子、比例因子等

2.确定各变量的语言值及其隶属函数

3.总结专家规则及其模糊关系，并选择模糊推理算法（Mamdani）

4.确定清晰化的方法（重心法）

5.总结成模糊查询表（精确输入E、EC的值与精确输出U的值的对应关系表）

参考教材：《智能控制原理与应用》.蔡自兴