Kalman Filter

古路

已于 2022-06-28 11:17:53 修改

阅读量2.1k

点赞数 2

分类专栏： # 滤波文章标签： Kalman Filter 卡尔曼滤波卡尔曼滤波推导

于 2019-07-10 17:36:02 首次发布

本文链接：https://blog.csdn.net/fb_941219/article/details/95340692

版权

滤波专栏收录该内容

9 篇文章 1 订阅

订阅专栏

Kalman Filter

0.引言

卡尔曼滤波（Kalman filtering）一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

Dynamic Model.

1.Kalman Filter

理论上，kalman滤波器需要三个重要假设：
1）被建模的系统是线性的；
2）影响测量的噪声属于白噪声；
3）噪声本质上是高斯分布的。

第一条假设是指 $k$ 时刻的系统状态可以用某个矩阵(状态转移矩阵)与 $k - 1$ 时刻的系统状态的乘积表示。余下两条假设，即噪声是高斯分布的白噪声，其含义为噪声与时间不相关，且只用均值和协方差就可以准确地为幅值建模。

在kalman滤波器滤波器应用中，一般考虑三种运动：
1）动态运动：这种运动是我们期望的前次测量时系统状态的直接结果，如匀速运动等。
2）控制运动：这种运动是我们期望的，由于某种已知的外部因素以某种原因施加于系统，如加速运动等。
3）随机运动：随机的无规则运动，在Kalman滤波器中，至少是可以用高斯模型有效地来建模。
在这里插入图片描述
以下建模中， $x_k$ 对应 $x_t$ ， $z_k$ 对应 $y_t$ .系统中带求解的即为状态量 $x_k$ 或者 $x_t$ 。

1.1. 建模

状态方程（运动方程）： $x_{k}=A x_{k-1}+B u_{k-1}+w_{k-1}$
观测方程（Landmark）： $z_{k}=H x_{k}+v_{k}$

假设测量方程中，测量传感器不止一种， $z_{k}$ 则为多维的列向量，包含每一种传感器的测量值，而每一种测量值都不准确（含有噪声）。卡尔曼滤波器的数据融合功能就正是体现在测量矩阵 $H$ 中。

$x (k)$ 是 $k$ 时刻的系统状态， $u (k)$ 是 $k$ 时刻对系统的控制量。 $A$ 是传输参数、 $B$ 是控制参数，都是系统参数，对于多模型系统，他们为矩阵。 $z (k)$ 是 $k$ 时刻的测量值， $H$ 是测量系统的参数，对于多测量系统， $H$ 为观测矩阵。 $w (k)$ 和 $v (k)$ 分别表示状态和测量的噪声。均假设为高斯白噪声，协方差分别是 $Q, R$ 。

协方差表达不确定性（噪声传递）
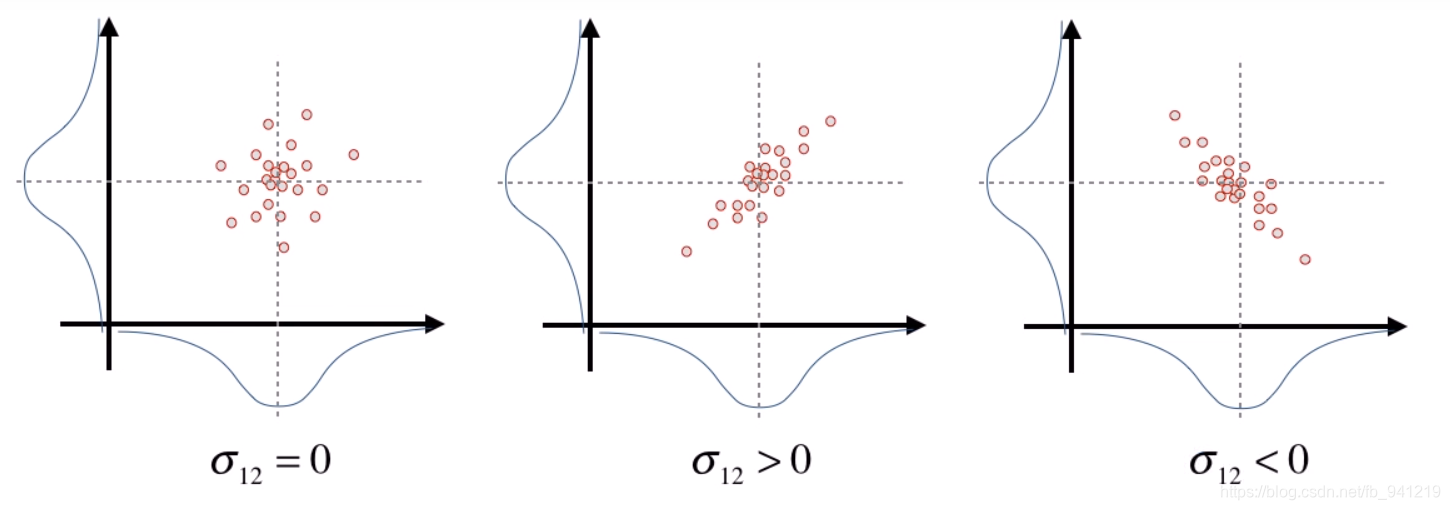$\operatorname{cov}(x, x)=\left[\begin{array}{cc}{\sigma_{11}} & {\sigma_{12}} \\ {\sigma_{12}} & {\sigma_{22}}\end{array}\right]$

1.2. 五个重要公式

- 系统模型

状态方程（运动方程）： $x_{k}=A x_{k-1}+B u_{k-1}+w_{k-1}$ , $p(w)\in N(0,Q)$
观测方程（Landmark）： $z_{k}=H x_{k}+v_{k}$ , $p(v)\in N(0,R)$

- 预测：
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\hat{x}_{k}^{-}=A \hat{x}_{k-1}+B u_{k-1} ~~~ ~~~~~~~~~~~(1)$

先验估计 $\hat{x}_{k}^{-}$ 为根据系统的转移方程计算所得，对比系统模型，少了过程噪声，因此并不是最佳的估计值。上一次的后验估计 $\hat{x}_{k-1}$ 。

$P_{k}^{-}=A P_{k-1} A^{T}+Q ~~~ ~~~~~~~~~~~~(2)$

$P_{k}^{-}$ 为先验误差协方差矩阵，是推导过程中产生的变量。 $P_{k}^{-}=E[e_k^{-}e_k^{-T}]$ ----> $e_k^{-}=x_k-\hat{x}_k^{-}$
$P_k$ 为后验误差协方差矩阵，是推导过程中产生的变量。 $P_k = E[e_ke_k^{T}]$ ----> $e_k=x_k-\hat{x}_k$
等式(2)实际为为噪声协方差的传递。

- 校正：
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~K_{k}=P_{k}^{-} H^{T}\left(H P_{k}^{-} H^{T}+R\right)^{-1}~~(3)$

$K_{k}$ 权衡预测量的协方差矩阵 $P$ 与观测量系协方差矩阵 $R$ 的大小，来决定系统是相信预测模型多一点还是相信测量模型多一点。
将残差的表现形式从观测域转换到状态域。即是卡尔曼系数 $K_k$ 解释了为什么可以用观测模型的值去更新状态模型中的值(两个域的量纲是不同的)。

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right)~~~~~~~~(4)$

$\left(z_{k}-H \hat{x}_{k}^{-}\right)$ 表示实际观测值与预测观测值的残差，乘上系数 $K_k$ （卡尔曼增益）就可以修正先验估计值 $\hat{x}_{k}^{-}$ 。
$\hat{x}_{k}$ ，后验估计值。就是最后需要的值。
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~P_{k}=\left(I-K_{k} H\right) P_{k}^{-}~~~~~~~~~~~~~~~~(5)$
最后这一个公式是在为下一轮的迭代做准备，噪声协方差矩阵的更新，这一步中，状态的不确定性是在减小的（校正），在下一轮根据状态方程传递（预测）时不确定性又会增大。

变量	含义
$\hat{x}_{k}^{-} = A \hat{x}_{k-1}+B u_{k-1}$	状态先验估计
$\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right)$	状态后验估计
$A$	状态转移矩阵
$B$	输入控制矩阵，外界的影响如何转化为对状态的影响
$u_{k-1} $	外部激励输入
$w_{k-1}\in N(0,Q)$	过程噪声, $Q$ =过程噪声协方差矩阵
$z_k$	$K$ 时刻的观测值
$H$	观测矩阵
$v_{k}\in N(0,R)$	测量噪声, $R$ =测量噪声协方差矩阵
$P_k = E[e_ke_k^{T}]$ ----> $e_k=x_k-\hat{x}_k$	（后验）误差协方差矩阵
$P_{k}^{-}=E[e_k^{-}e_k^{-T}]$ ----> $e_k^{-}=x_k-\hat{x}_k^{-}$	先验误差协方差矩阵
$K_{k}=P_{k}^{-} H^{T}\left(H P_{k}^{-} H^{T}+R\right)^{-1}$	kalman增益

推导参考.
在这里插入图片描述

2.推导

请添加图片描述

3.MatlabDemo

参考百度百科

小车运动模型：

Z=(1:100);%观测值
noise=randn(1,100);%方差为1 的噪声
Z=Z+noise;

X=[0;0];%状态
P=[1 0;0 1];%状态协方差
F=[1 1;0 1];%状态转移矩阵
Q=[0.0001,0;0 0.0001];%状态转移矩阵协方差
H=[1 0];%观测矩阵
R=1;%观测噪声方差

figure;
hold on 
for i=1:100
    X_ = F*X;
    P_ = F*P*F' + Q;
    K = P_*H'/(H*P_*H'+R);
    X = X_+K*(Z(i)-H*X_);
    P = (eye(2)-K*H)*P_;
    
    plot(X(1),X(2),'.'); %画点，横轴表示位置，纵轴表示速度

end

状态量：速度。观测量：位置。
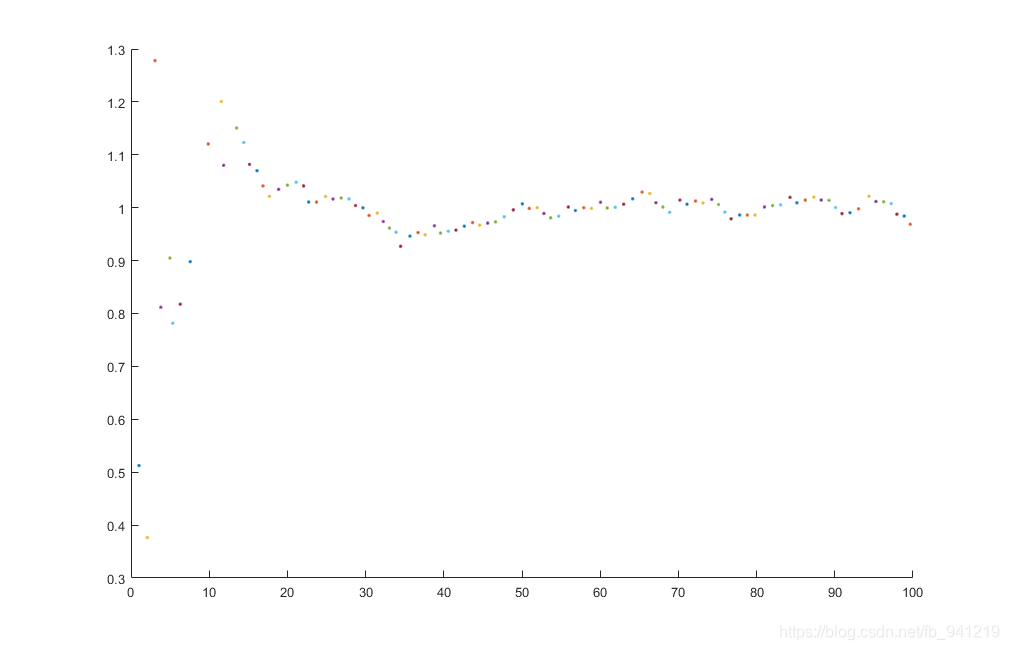
在这里插入图片描述

DEMO2

%房间当前温度真实值为24度，认为下一时刻与当前时刻温度相同，误差为0.02度（即认为连续的两个时刻最多变化0.02度）。
%温度计的测量误差为0.5度。
%开始时，房间温度的估计为23.5度，误差为1度。
clear all;
close all;
% intial parameters
n_iter = 100; %计算连续n_iter个时刻
sz = [n_iter, 1]; % size of array. n_iter行，1列
x = 24; % 度的真实值
Q = 4e-4; % 过程方差， 反应连续两个时刻温度方差。更改查看效果
R = 0.25; % 测量方差，反应温度计的测量精度。更改查看效果
z = x + sqrt(R)*randn(sz); % z是温度计的测量结果，在真实值的基础上加上了方差为0.25的高斯噪声。
% 对数组进行初始化
xhat=zeros(sz); % 对温度的后验估计。即在k时刻，结合温度计当前测量值与k-1时刻先验估计，得到的最终估计值
P=zeros(sz); % 后验估计的方差
xhatminus=zeros(sz); % 温度的先验估计。即在k-1时刻，对k时刻温度做出的估计
Pminus=zeros(sz); % 先验估计的方差
K=zeros(sz); % 卡尔曼增益，反应了温度计测量结果与过程模型（即当前时刻与下一时刻温度相同这一模型）的可信程度
% intial guesses
xhat(1) = 23.5; %温度初始估计值为23.5度
P(1) =1; %误差方差为1
for k = 2:n_iter
% 时间更新（预测）
xhatminus(k) = xhat(k-1); %用上一时刻的最优估计值来作为对当前时刻的温度的预测
Pminus(k) = P(k-1)+Q; %预测的方差为上一时刻温度最优估计值的方差与过程方差之和
% 测量更新（校正）
K(k) = Pminus(k)/( Pminus(k)+R ); %计算卡尔曼增益
xhat(k) = xhatminus(k)+K(k)*(z(k)-xhatminus(k)); %结合当前时刻温度计的测量值，对上一时刻的预测进行校正，得到校正后的最优估计。该估计具有最小均方差
P(k) = (1-K(k))*Pminus(k); %计算最终估计值的方差
end
FontSize=14;
LineWidth=3;
figure();
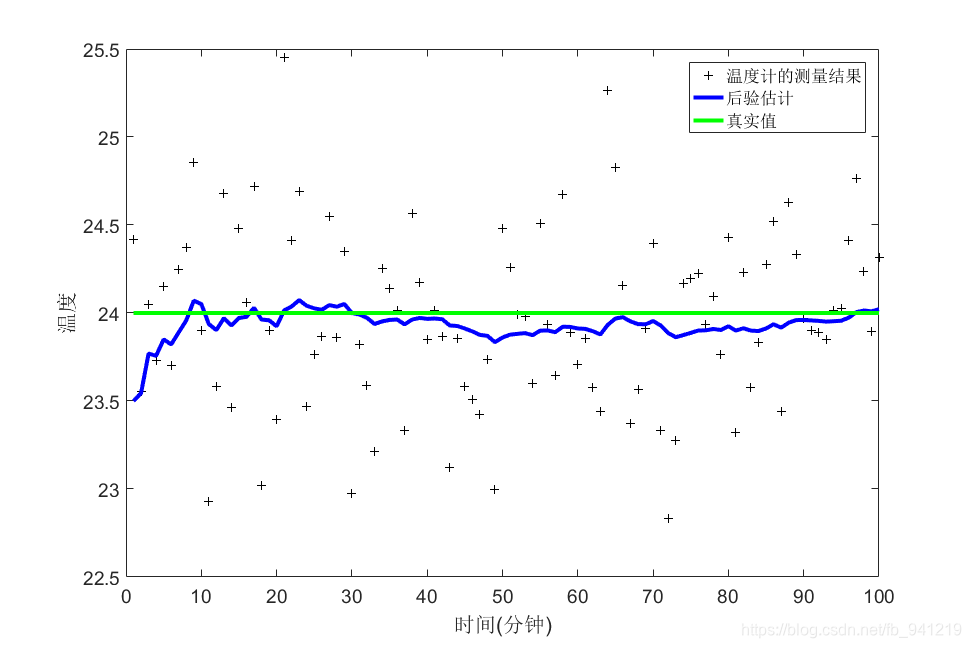
plot(z,'k+'); %画出温度计的测量值

hold on;
plot(xhat,'b-','LineWidth',LineWidth) %画出最优估计值
hold on;
plot(x*ones(sz),'g-','LineWidth',LineWidth); %画出真实值
legend('温度计的测量结果', '后验估计', '真实值');
xl=xlabel('时间(分钟)');
yl=ylabel('温度');
set(xl,'fontsize',FontSize);
set(yl,'fontsize',FontSize);
hold off;
set(gca,'FontSize',FontSize);
figure();
valid_iter = [2:n_iter]; % Pminus not valid at step 1
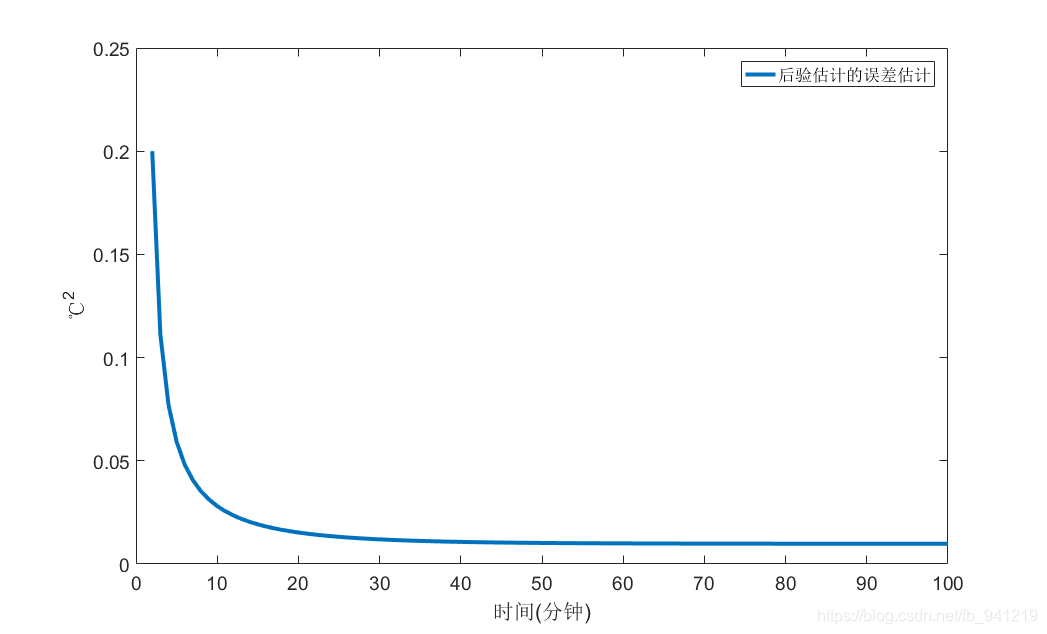
plot(valid_iter,P([valid_iter]),'LineWidth',LineWidth); %画出最优估计值的方差
legend('后验估计的误差估计');
xl=xlabel('时间(分钟)');
yl=ylabel('℃^2');
set(xl,'fontsize',FontSize);
set(yl,'fontsize',FontSize);
set(gca,'FontSize',FontSize);

在这里插入图片描述

DEMO3
徐老师demo，同样是小车二维运动，描述在PPT上：

% --------------------------------------
% Kalman Filter demos
% written by Richard Xu
% yida.xu@uts.edu.au, July, 2014
% --------------------------------------

clc;
clear;

% --------------------------------------------------------------------
% Synthetically generate data from nominated Kalman Filter parameters
% --------------------------------------------------------------------

% for p(x_1)初始化参数
init_mu  = [ 0 0]';
init_var = [ 5 0; 0 5];      

% transition probability 运动方程
A = [1 0; 0 1];
B = [0.2 0.1]';
Q = [0.1 0.05; 0.05 0.1];
%Q = [1E-5 0; 0 1E-5];
% fixed parameters 测量方程
H = [1 0; 0 1];
R = [0.5 -0.05; -0.05 0.5];
%R = [1E-5 0 ; 0 1E-5];
T = 16;  %测量数据次数
xs(1,:) = [0 0];%初始状态量，位置+速度
for t=2:T 
   xs(t,:) = (A * xs (t-1,:)')' + B' + mvnrnd([0 0], Q );
end
% data is a sequence of y  观测值
data = xs + mvnrnd([0 0],R,T);
data = data';

%update = Kalman_posterior (data, A, B, Q, H, R, T, init_mu, init_var);

update_mu       = zeros(2,T);
update_Sigma    = zeros(2,2,T);

predict_mu       = zeros(2,T);
predict_Sigma    = zeros(2,2,T);

for t=1:T
        
    % --------------------------------
    % Kalman Filter update
    % --------------------------------
    
    if t == 1
        predict_mu(:,1)         = init_mu;
        predict_Sigma(:,:,1)    = init_var;
    else
        predict_mu(:,t)         = A * update_mu(:,t-1) + B;% 等式（1）
        predict_Sigma(:,:,t)    = A * update_Sigma(:,:,t-1) * A' + Q;  %等式（2）
    end

    S = H * predict_Sigma(:,:,t) * H' + R;   
    K = predict_Sigma(:,:,t) * H' * inv(S); %等式（3）
   
    update_mu(:,t)      = predict_mu(:,t) + K * (data(:,t) - H * predict_mu(:,t));  %等式（4）
    update_Sigma(:,:,t) = (eye(size(R,2)) - K * H ) * predict_Sigma(:,:,t);  %等式（5）
    
    %display(update_mu(:,t));
    display(update_Sigma(:,:,t));
       
    % --------------------------------
    % The plot  绘图演示，以下可以不用管，只是为了演示
    % --------------------------------   
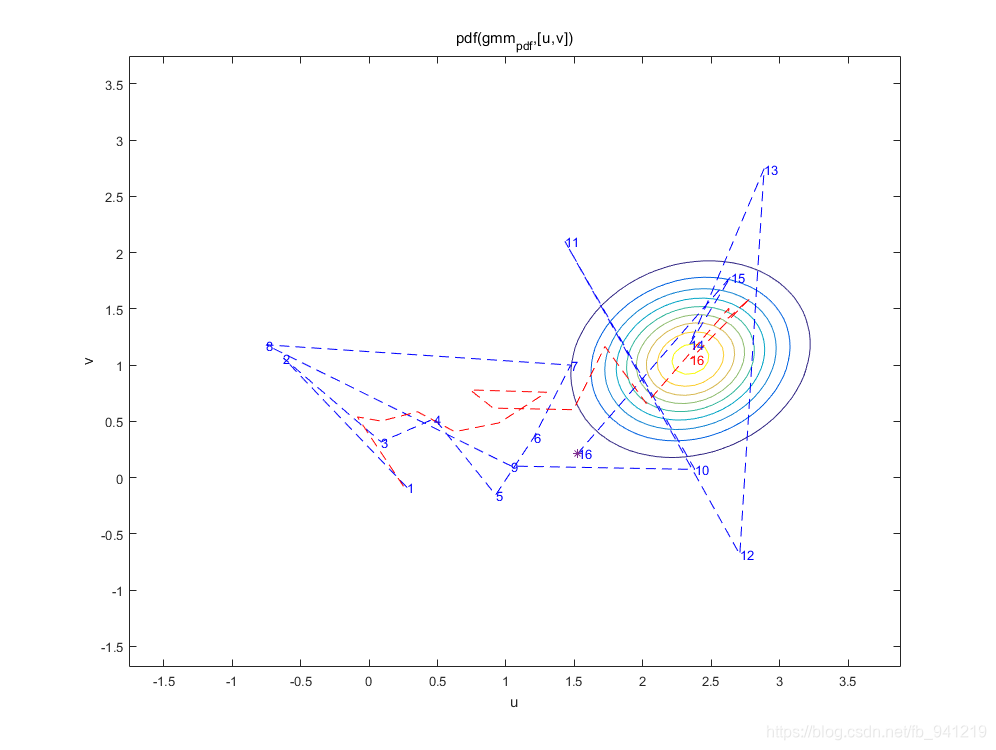
    gmm_pdf = gmdistribution(update_mu(:,t)',update_Sigma(:,:,t),1); 
    ezcontour(@(u,v)pdf(gmm_pdf,[u v]));
    hold on;
    
    plot(data(1,1:t),data(2,1:t),'--','color',[0 0 1]);
    axis([min(data(1,:))-1 max(data(1,:))+1 min(data(2,:))-1 max(data(2,:))+1]); 
    hold on;
    
    plot(update_mu(1,1:t),update_mu(2,1:t),'--','color',[1 0 0]);
    text(update_mu(1,t),update_mu(2,t), num2str(t), 'color', [ 1 0 0]);
    
    axis([min(data(1,:))-1 max(data(1,:))+1 min(data(2,:))-1 max(data(2,:))+1]); 
    hold on;
    
    plot(data(1,t:T),data(2,t:T),'--','color',[0.7 0.7 0.7]);
    axis([min(data(1,:))-1 max(data(1,:))+1 min(data(2,:))-1 max(data(2,:))+1]); 
    hold on;
    
    plot(data(1,t),data(2,t),'*');
    
    for s=1:T
        text(data(1,s),data(2,s), num2str(s), 'color',[ 0 0 1]);
        hold on;
    end
       
    
    hold off;
    waitforbuttonpress;
end

在这里插入图片描述

DEMO4：
同样是小车模型，状态量为速度+位置，测量为位置。模型推导在徐老师PPT里面也有推导，也可以参考这篇文章。

% Kalman Example 1
 
dt = 1;
 
P = [ 25, 0;
       0, 1; ];
 
X = [ 0;
      0; ];
 
R = [ 1; ];
 
F = [ 1, dt;
      0, 1; ];
 
H = [ 1, 0; ];
Q = (1e-6) * [ (dt^4)/4, (dt^3)/2;
                 (dt^3)/2, dt^2; ];
 
pos = 0;
velocities = zeros(1, 100);
positions = zeros(1, 100);
truePositions = zeros(1, 100);
for i = 1 : 100
    Xp = F*X;
    Pp = F*P*F' + Q;
 
    K = (Pp*H')/(H*Pp*H' + R);
    y = (pos+randn()) - H*Xp;
 
    X = Xp + K*y;
    P = Pp - K*H*Pp;
 
    velocities(i) = X(2);
    positions(i) = X(1);
    truePositions(i) = pos;
 
    pos = pos + 0.1;
end
 
plot(linspace(0, 100, 100), velocities, 'r');
title('Estimated Velocity');
xlabel('s')
ylabel('m/s');
 
figure;
plot(linspace(0, 100, 100), positions, 'r');
title('Estimated Position');
xlabel('s')
ylabel('m');

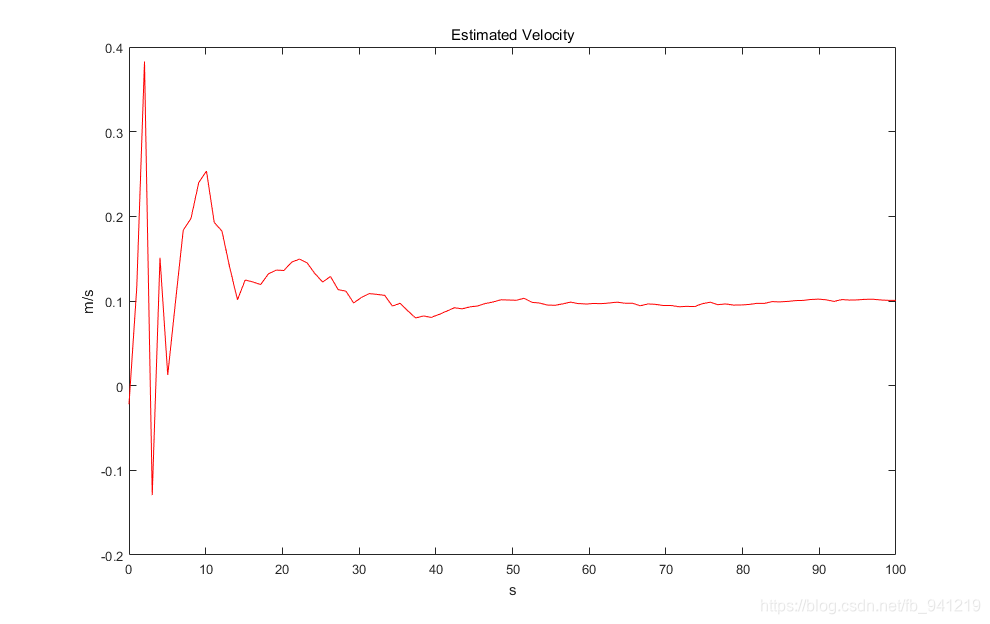
在这里插入图片描述

迭代过程如上图所示，状态量速度逐渐稳定在0.1左右，状态量位置逐渐稳定为线性模型。

古路

关注

2
点赞
踩
14

收藏

觉得还不错? 一键收藏
0
评论
Kalman Filter

Kalman01 Filter0.引言1.Kalman Filter1.1. 建模1.2. 五个重要公式2.MatlabDemo0.引言卡尔曼滤波（Kalman filtering）一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。Kalman.1.Kalman Filter理论上......
复制链接

扫一扫