Fouier Net和DeepOnet等求解器算法解读和代码

谨慎付费（看不懂试读博客不要订阅）

已于 2024-11-27 20:39:18 修改

阅读量4.7k

点赞数 8

分类专栏： Deep learning 文章标签：算法 python 深度学习

于 2022-11-21 16:04:32 首次发布

本文链接：https://blog.csdn.net/forrestguang/article/details/127966413

版权

Deep learning 专栏收录该内容

42 篇文章 ¥239.90 ¥399.90

订阅专栏

本文探讨了使用深度学习解决偏微分方程的两种方法：Fouier神经网络（FNO）和DeepOnet。通过FNO的傅里叶块和DeepOnet的结构解读，展示了它们如何处理不同右端项的求解。同时，介绍了数据驱动的损失函数思想，并讨论了各自的优缺点以及在实际应用中的性能表现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

博客内容参考知乎添加链接描述

问题描述

首先还是先给定一个泊松方程，其中区域 $Ω=[0,1+μ_1]×[0,1],μ_1∈[1,3]$ ，边界条件 $g = 1$ 。
$Δu=f,x∈Ω=[0,1+μ_1]×[0,1],μ_1∈[1,3],\\ u|∂Ω=g=1.$
以往的传统数值方法都是针对固定的一个右端项求出一个对应的数值解，这种做法的核心是构造一个输入节点数目为2，输出节点数目为1的模型（有限元句柄函数或者全连接神经网络），基于此科学家设计了许多诸如PINN,Galerkin的方法，这类方法往往根据物理模型构造出一个线性或者非线性系统，或者NN的损失函数，然后不断优化求解。这类算法的特点是，对于每一个固定的右端项函数，都可以以相对快速的速度求出一个近似解，但是每一个右端项函数的出现，都需要重新进行数值仿真。
是否可以给出一个模型，该模型可以根据右端项 f(x,y) 的数学形式直接给出近似解的表达式？偏微分方程求解器就是这样的一个工作。
偏微分方程求解器的基本理念
设计一个模型，接受的输入是 $f(x_i,y_j),x_i,y_j)$ ，输出近似解 $u(x_i,y_j)$ ，也就是说现在假设了一个映射关系：G，使得 $G(f(x_i,y_j),x_i,y_j)=u(x_i,y_j)$ 。为了得到这个模型G的具体表达，现有的几类方法都是使用神经网络来拟合G，最简单的模型莫过于全连接神经网络。和之前一样，我们定义一个全连接神经网络 $G(f(x_i,y_j),x_i,y_j;θ)$ ，这个模型的输入节点数目是3，输出节点数目是1，下面考虑如何优化该模型里面的参数 θ 使得这个模型尽可能满足 $G(f(x_i,y_j),x_i,y_j;θ)=u(x_i,y_j)$
这里先给出数据生成的代码：
data.py

import torch
import numpy as np
import torch.nn as nn
from scipy.stats import qmc

mu1 = 2
hr = 1e-2
bound = np.array([0 + hr,1 + mu1 - hr,0 + hr,1 - hr]).reshape(2,2)
class Net(torch.nn.Module):
    def __init__(self, layers, dtype):
        super(Net, self).__init__()
        self.layers = layers
        self.layers_hid_num = len(layers)-2
        
        self.dtype = dtype
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
    def forward(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])  
class LEN():
    def __init__(self):
        pass
    def forward(self,x):
        
        x1 = x[:,0:1]
        x2 = x[:,1:2]
        L = (x1 - bound[0,0])*(bound[0,1] - x1)*(x2 - bound[1,0])*(bound[1,1] - x2)
        return L.reshape(-1,1)
len_data = LEN()
def function_u(net_data,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    return net_data.forward(x)*len_data.forward(x) + 1
def function_f(net_data,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    state = function_u(net_data,len_data,x)
    state_x, = torch.autograd.grad(state,x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))
    state_xx, = torch.autograd.grad(state_x[:,0:1],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1])) 
    state_yy, = torch.autograd.grad(state_x[:,1:2],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))     
    state_lap = state_xx[:,0:1] + state_yy[:,1:2]
    x.requires_grad = False
    return -state_lap.data     
                                                                       
class INdata():
    def __init__(self,data_size,fun_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(data_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_u = torch.zeros(fun_size,data_size)
        self.data_f = torch.zeros(fun_size,data_size)
        for i in range(fun_size):
            np.random.seed(seeds + 10*i)
            torch.manual_seed(seeds + 10*i)
            net_data = Net(layers,dtype)
            
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,self.x).t()
            self.data_f[i:i + 1,:] = function_f(net_data,len_data,self.x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample

data_size = 32*32
fun_size = 20
lay_wid = 20
layers = [2,lay_wid,lay_wid,lay_wid,1]
dtype = torch.float32
seeds = 0
indata = INdata(data_size,fun_size,layers,dtype,seeds)
'''
np.save('data_u.npy',indata.data_u.detach().numpy())
np.save('data_f.npy',indata.data_f.detach().numpy())
np.save('data_x.npy',indata.x.detach().numpy())

'''
np.save('./data_u.npy',indata.data_u.detach().numpy())
np.save('./data_f.npy',indata.data_f.detach().numpy())
np.save('./data_x.npy',indata.x.detach().numpy())

两种损失函数的思想

PINN
在这里插入图片描述
这种思想非常简单且直观，对于许多数学系的同学都能看懂，下面我们来分析一下这种做法的代码编写和具体的训练过程：
1：形成损失函数的过程中，对于每一个右端项都需要求对应的二阶偏导数，这个过程只能通过for循环来实现，伪代码如下，这里也暴露出pytorch的一个特点，pytorch无法针对这样的一个三维矩阵求梯度，因此必须要使用for循环才能完成这个过程。当N很大的时候，形成损失函数的时间将会非常恐怖，后面训练的时候，每做一次参数 θ 的更新，损失函数就需要重新形成一次，这个耗时对于大部分人来说难以忍受。

inset.X = [N,S,3]#N个右端项，在区域内部采集S个坐标点，注意排列方式是[f,x,y]
G = [N,S,1]#表示模型对应的N个右端项在S个坐标点的近似解
f = [N,S,1]#表示N个右端项在S个坐标点的取值
L = 0
for i in range(N):
    G_x, = torch.autograd.grad(G, inset.X, create_graph=True, retain_graph=True,
                                 grad_outputs=torch.ones(inset.X.shape[1],1).to(device))
    G_xx, = torch.autograd.grad(G_x[:,1:2], inset.X, create_graph=True, retain_graph=True,
                                 grad_outputs=torch.ones(inset.X.shape[1],1).to(device))
    G_yy, = torch.autograd.grad(G_x[:,2:3], inset.X, create_graph=True, retain_graph=True,
                                 grad_outputs=torch.ones(inset.X.shape[1],1).to(device))
    G_lap = G_xx[:,1:2] + G_yy[:,2:3]
    L += ((G_lap + f[i])**2).mean()

2：但是这种做法的好处就在于，只需要给定右端项f就可以形成损失函数，得到N个右端项f和对应样本点的取值总是很容易的。
下面我们来看一看另一种数据驱动的方法是怎么做的。
data-driven
PINN的思想虽然简单，但是由于需要对庞大的数据反向传播，整个loss function的形成耗时严重，制约了这个方法的性能，为了避免反向传播，这里引入数据驱动的思想。和上面相同的是，我们仍然需要从函数空间里面选取 N 个右端项： $f_0,f_1,…,f_{N−1}$ ，但是这里我们根据右端项函数的具体形式和样本点的位置，利用高精度数值方法（有限元，差分法）或者现有的数值求解器OpenFoam等得到N个近似解 $u_0,u_1,…,u_{N−1}$ ，然后根据样本点的位置得到一个形状为[N,S,1]的标签u，这个标签存储的是N个近似解在S个样本点的取值，理论上，我们要求标签里面的近似解取值严格满足对应的PDE（但是实际操作中，如果我们使用五点差分法，也可以得到这样的标签u，且标签和真实解的误差在 $O(h^2)$ 控制范围内）。
在这里插入图片描述
这个损失函数很简单，后面的训练也会容易很多，特别适合大规模的问题。我们也来分析一下这个思想的具体问题和优势：
1：这个做法其实有一些舍本逐末，我们本来就需要得到不同右端项下的近似解，但是这个思想却要求先提供不同右端项对应的高精度近似解，如果我们都有高精度的近似解形成方法（比如Openfoam可以给较高精度的近似解u)，那么这个模型G的存在仿佛就意义不大。
在这里插入图片描述
对于第一个问题，有人给出了一个说法，虽然目前有OpenFoam等求解器，但是这些求解器速度比较慢，比如说我根据五点差分法构造了一个求解F， $F (f) = u$ ，我们知道五点差分法求解需要构建线性系统，还要求解线性系统，如果剖分很大，线性系统求解时间肯定也不少，但是如果我们训练好了这样一个模型G，发现 $G (f, x, y) = u$ ，这个过程利用的是正向传播，这个速度肯定更快，这个也就是这个工作的意义，只要训练好了模型G，求解PDE的过程就相当于直接调用一个早就做好的句柄函数，速度非常惊人。
对于第二个问题，鄙人一直没看见什么好的解释。下面不妨来看一看几个经典的工作和代码的实现，下面介绍的几个工作都是基于data-driven的。
这里重点说明，右端项f来自一个无限维空间，如果求解器要有很好的效果，那么f一定要选取尽可能多，但是对于大部分人来说，计算资源不足以支撑大规模的训练，这里展示代码的时候，本人都假设右端项f是一个全连接神经网络构造的句柄函数，即f=Net(x,y),Net是一个全连接神经网络，此时f属于的函数空间就变成了一个有限维的函数空间，自由度就是神经网络的参数数目。我们希望求解器G最终可以做到，对任意一个 $f = N e t (x, y)$ ，都有 $G (f, x, y)$ 满足对应的PDE约束。

DeepOnet解读

参考文献是：DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators
在这里插入图片描述
代码实现的具体参数意义如下：
fun_size:选取的右端项数目，也就是上面提到的 N
data_size:区域内采集的训练样本点数目，也就是上面提到的 S
1：定义一个神经网络Net，给定长度因子 l ，定义一个y的近似解句柄函数为 ytrain=Net∗l+1 。
2：利用pytorch反向传播，定义u的近似解句柄函数 utrain ，这样就可以这么说，对于每一个右端项 utrain ，我们都得到了一个对应的标签解 ytrain=Net∗l+1 ，这个标签解满足边界条件，由刚才 utrain 的定义我们知道这个标签解也满足PDE，根据解的存在唯一性定理，我们也就是说通过这种方式得到一对数据 (utrain,ytrain) .
因此我们得到了data_y=[N,S],data_u = [N,S],data_x = [S,2]的训练数据。
brank接受的输入就是data_u=[N,S]，输出的形状是[N,K]，假设输出是bra；
trunk接受的输入是data_x = [S,2]，输出的形状是[S,K]，假设输出是tru；
最终我们希望的输出维度应该是[N,S]表示这N个右端项在S个样本点的取值，输出的就应该是bra@tru.t()
DeepOnet.py

import torch
import numpy as np
import torch.nn as nn
import time
from data import *
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#device = torch.device('cpu')
dtype = torch.float32

fname_y = "data_u.npy"
fname_u = "data_f.npy"
fname_x = "data_x.npy"

data_u = np.load(fname_y)
data_f = np.load(fname_u)
data_x = np.load(fname_x)

class Solvernet(torch.nn.Module):
    def __init__(self, data_size,input_dim,output_dim,layers, dtype):#注意这里的layers只是hidden
        super(Solvernet, self).__init__()
        
        
        self.dtype = dtype
        #------------------------
        self.kernel_size = [10,6,10]
        self.stride = [1,2,2]
        cov = []
        out_dim = [3,1,1]
        in_dim = 1

        for i in range(len(self.kernel_size)):
            cov.append(nn.Conv1d(in_channels = in_dim,out_channels = out_dim[i],kernel_size = self.kernel_size[i],stride = self.stride[i]))
            data_size = (data_size - self.kernel_size[i])//self.stride[i] + 1
            in_dim = out_dim[i]
        self.cov = torch.nn.Sequential(*cov)
        for i in range(len(self.kernel_size)):
            self.cov[i].weight.data = self.cov[i].weight.data.type(dtype)
            self.cov[i].bias.data = self.cov[i].bias.data.type(dtype)
        #------------------------
        #-------branch DNN
        self.bra_layers = [data_size] + layers + [output_dim]
        
        self.bra_layers_hid_num = len(self.bra_layers)-2
        bra_fc = []
        for i in range(self.bra_layers_hid_num+1):
            bra_fc.append(torch.nn.Linear(self.bra_layers[i],self.bra_layers[i+1]))
            bra_fc.append(torch.nn.Linear(self.bra_layers[i + 1],self.bra_layers[i+1]))
        bra_fc.append(torch.nn.Linear(self.bra_layers[-2],self.bra_layers[-1]))
        self.bra_fc = torch.nn.Sequential(*bra_fc)
        for i in range(self.bra_layers_hid_num+1):
            self.bra_fc[2*i].weight.data = self.bra_fc[2*i].weight.data.type(dtype)
            self.bra_fc[2*i].bias.data = self.bra_fc[2*i].bias.data.type(dtype)
            self.bra_fc[2*i + 1].weight.data = self.bra_fc[2*i + 1].weight.data.type(dtype)
            self.bra_fc[2*i + 1].bias.data = self.bra_fc[2*i + 1].bias.data.type(dtype)
        self.bra_fc[-1].weight.data = self.bra_fc[-1].weight.data.type(dtype)
        self.bra_fc[-1].bias.data = self.bra_fc[-1].bias.data.type(dtype)
        #------------------------
        self.layers = [input_dim] + layers + [output_dim]
        self.layers_hid_num = len(self.layers)-2
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
        
    def CNN(self,x):
        h = x.reshape(x.shape[0],1,x.shape[1])
        for i in range(len(self.cov)):
            h = self.cov[i](h)
            h = torch.sin(h)
        #print(h.shape)
        return h.squeeze(dim = 1)
    def branch(self,data_f):
        
        x = self.CNN(data_f)
        dev = x.device
        for i in range(self.bra_layers_hid_num):
            h = torch.sin(self.bra_fc[2*i](x))
            
            h = torch.sin(self.bra_fc[2*i+1](h))
            
            temp = torch.eye(x.shape[-1],self.bra_layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.bra_fc[-1](x)
    def trunk(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    
    def forward(self,data_f,x):
        bra = self.branch(data_f)
        tru = self.trunk(x)
        
        #print(bra.shape,tru.shape,(bra@tru.t()).shape)
        return bra@tru.t()
        
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])  

def pred_y(solvernet,data_f,x):
    return solvernet.forward(data_f,x)
def Loss(solvernet,data_f,x,data_u):
    y = pred_y(solvernet,data_f,x)
    err = ((y - data_u)**2).sum()
    return torch.sqrt(err)
def train_yp(solvernet,data_f,x,data_u,optim,epoch):
    print('Train y&p Neural Network')
    loss = Loss(solvernet,data_f,x,data_u)
    print('epoch:%d,loss:%.2e, time: %.2f'
          %(0, loss.item(), 0.00))
    for it in range(epoch):
        st = time.time()
        def closure():
            loss = Loss(solvernet,data_f,x,data_u)
            optim.zero_grad()
            loss.backward()
            return loss
        optim.step(closure) 
        loss = Loss(solvernet,data_f,x,data_u)
        ela = time.time() - st
        print('epoch:%d,loss:%.2e, time: %.2f'
              %((it+1), loss.item(), ela))
def predata(data_f,data_u,data_x,solvernet,dev):
    data_f = torch.tensor(data_f).type(dtype)
    data_u = torch.tensor(data_u).type(dtype)
    data_x = torch.tensor(data_x).type(dtype)
    data_f = data_f.to(dev)
    data_u = data_u.to(dev)
    data_x = data_x.to(dev)
    solvernet = solvernet.to(dev)

data_size = data_u.shape[1]
input_dim = 2
output_dim = 9
layers = [15,15]
solvernet = Solvernet(data_size,input_dim,output_dim,layers, dtype)

fname1 = "lay%d-ynet-var.pt"%(output_dim)
#fname1 = ".//deeponet//lay%d-ynet-var.pt"%(output_dim)
#predata(data_f,data_u,data_x,solvernet,device)
data_f = torch.tensor(data_f).type(dtype)
data_u = torch.tensor(data_u).type(dtype)
data_x = torch.tensor(data_x).type(dtype)
data_f = data_f.to(device)
data_u = data_u.to(device)
data_x = data_x.to(device)
print(data_f.shape,data_u.shape,data_x.shape)
solvernet = solvernet.to(device)
lr = 1e-1
optim = torch.optim.LBFGS(solvernet.parameters(),
                      lr=lr, max_iter=100,
                      tolerance_grad=1e-16, tolerance_change=1e-16,
                      line_search_fn='strong_wolfe')
epoch = 1
#rint(type(data_u),type(data_f),type(data_x))
y = solvernet.forward(data_f,data_x)
train_yp(solvernet,data_f,data_x,data_u,optim,epoch)
torch.save(solvernet,fname1)
solvernet = torch.load(fname1)
#-----test
class Testdata():
    def __init__(self,data_x,data_size,fun_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(data_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_u = torch.zeros(fun_size,data_size)
        self.data_f = torch.zeros(fun_size,data_x.shape[0])
        for i in range(fun_size):
            np.random.seed(seeds + i)
            torch.manual_seed(seeds + i)
            net_data = Net(layers,dtype)
            
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,self.x).t()
            self.data_f[i:i + 1,:] = function_f(net_data,len_data,data_x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample

test_size = 32*64
fun_size = 3
lay_wid = 20
testseeds = data_size
layers = [2,lay_wid,lay_wid,1]

test = Testdata(data_x.to('cpu'),test_size,fun_size,layers,dtype,testseeds)
solvernet = solvernet.to('cpu')
y = solvernet.forward(test.data_f,test.x)
y_acc = test .data_u
err = (y - y_acc).reshape(-1,1)
L1 = max(abs(err))
L2 = (err**2).sum()
print('test error:L1:%.2e,L2:%.2e'%(L1,L2))

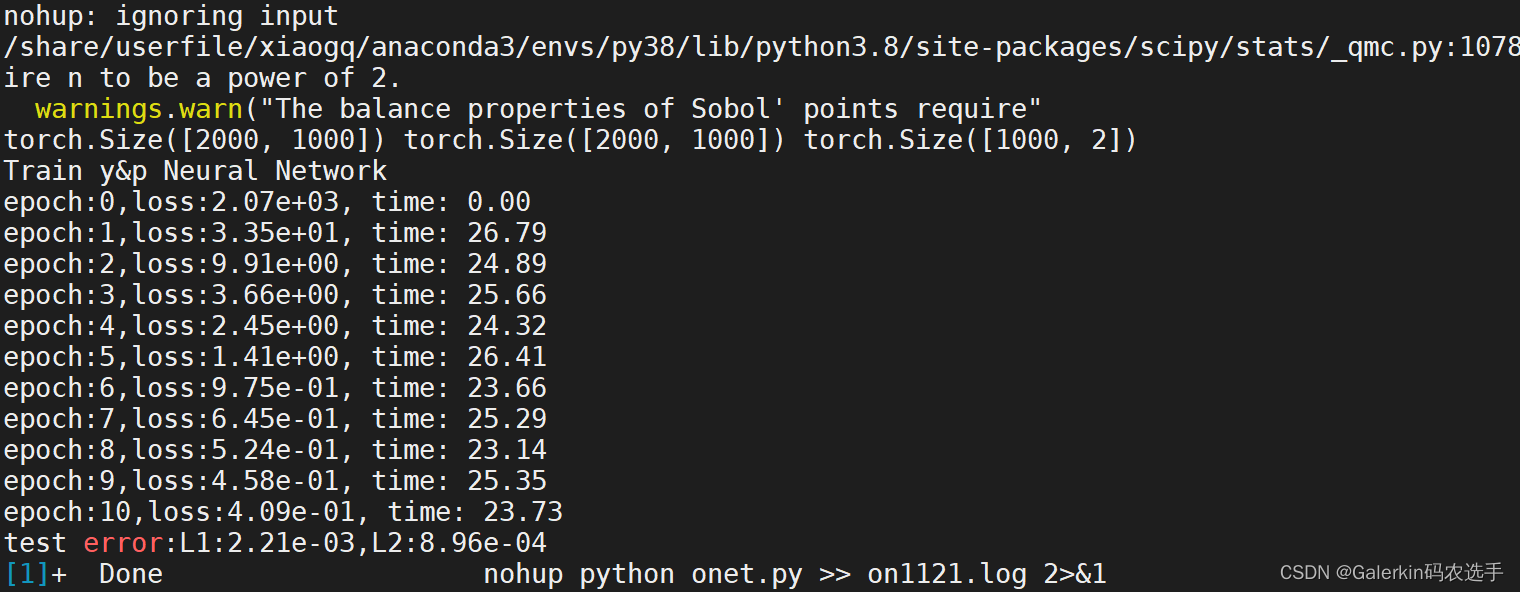
在这里插入图片描述
上面这个是本人实现的DeepOnet.py的训练过程，发现对于这种右端项泛化能力非常不错。
本人的测试集代码如下：
deeptest.py

import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F

from scipy.stats import qmc
#device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device = torch.device('cpu')
dtype = torch.float32
'''
fname_y = "data_y.npy"
fname_x = "data_x.npy"
'''
fname_y = "C://Users//2001213226//Desktop//graduation//deeponet//data_y.npy"

fname_x = "C://Users//2001213226//Desktop//graduation//deeponet//data_x.npy"

data_y = np.load(fname_y)
data_x = np.load(fname_x)

mu1 = 2
hr = 1e-2
bound = np.array([0 + hr,1 + mu1 - hr,0 + hr,1 - hr]).reshape(2,2)
class Net(torch.nn.Module):
    def __init__(self, layers, dtype):
        super(Net, self).__init__()
        self.layers = layers
        self.layers_hid_num = len(layers)-2
        
        self.dtype = dtype
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
    def forward(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])  
class LEN():
    def __init__(self):
        pass
    def forward(self,x):
        
        x1 = x[:,0:1]
        x2 = x[:,1:2]
        L = (x1 - bound[0,0])*(bound[0,1] - x1)*(x2 - bound[1,0])*(bound[1,1] - x2)
        return L.reshape(-1,1)
len_data = LEN()
def function_y(net_data,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    return net_data.forward(x)*len_data.forward(x) + 1
def function_u(net_data,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    state = function_y(net_data,len_data,x)
    state_x, = torch.autograd.grad(state,x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))
    state_xx, = torch.autograd.grad(state_x[:,0:1],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1])) 
    state_yy, = torch.autograd.grad(state_x[:,1:2],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))     
    state_lap = state_xx[:,0:1] + state_yy[:,1:2]
    x.requires_grad = False
    return -state_lap.data     
                                                                       


class Solvernet(torch.nn.Module):
    def __init__(self, data_size,input_dim,output_dim,layers, dtype):#注意这里的layers只是hidden
        super(Solvernet, self).__init__()
        
        
        self.dtype = dtype
        #------------------------
        self.kernel_size = [10,6,10]
        self.stride = [1,2,2]
        cov = []
        out_dim = [3,1,1]
        in_dim = 1

        for i in range(len(self.kernel_size)):
            cov.append(nn.Conv1d(in_channels = in_dim,out_channels = out_dim[i],kernel_size = self.kernel_size[i],stride = self.stride[i]))
            data_size = (data_size - self.kernel_size[i])//self.stride[i] + 1
            in_dim = out_dim[i]
        self.cov = torch.nn.Sequential(*cov)
        for i in range(len(self.kernel_size)):
            self.cov[i].weight.data = self.cov[i].weight.data.type(dtype)
            self.cov[i].bias.data = self.cov[i].bias.data.type(dtype)
        #------------------------
        #-------branch DNN
        self.bra_layers = [data_size] + layers + [output_dim]
        
        self.bra_layers_hid_num = len(self.bra_layers)-2
        bra_fc = []
        for i in range(self.bra_layers_hid_num+1):
            bra_fc.append(torch.nn.Linear(self.bra_layers[i],self.bra_layers[i+1]))
            bra_fc.append(torch.nn.Linear(self.bra_layers[i + 1],self.bra_layers[i+1]))
        bra_fc.append(torch.nn.Linear(self.bra_layers[-2],self.bra_layers[-1]))
        self.bra_fc = torch.nn.Sequential(*bra_fc)
        for i in range(self.bra_layers_hid_num+1):
            self.bra_fc[2*i].weight.data = self.bra_fc[2*i].weight.data.type(dtype)
            self.bra_fc[2*i].bias.data = self.bra_fc[2*i].bias.data.type(dtype)
            self.bra_fc[2*i + 1].weight.data = self.bra_fc[2*i + 1].weight.data.type(dtype)
            self.bra_fc[2*i + 1].bias.data = self.bra_fc[2*i + 1].bias.data.type(dtype)
        self.bra_fc[-1].weight.data = self.bra_fc[-1].weight.data.type(dtype)
        self.bra_fc[-1].bias.data = self.bra_fc[-1].bias.data.type(dtype)
        #------------------------
        self.layers = [input_dim] + layers + [output_dim]
        self.layers_hid_num = len(self.layers)-2
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
        
    def CNN(self,x):
        h = x.reshape(x.shape[0],1,x.shape[1])
        for i in range(len(self.cov)):
            h = self.cov[i](h)
            h = torch.sin(h)
        #print(h.shape)
        return h.squeeze(dim = 1)
    def branch(self,data_u):
        
        x = self.CNN(data_u)
        dev = x.device
        for i in range(self.bra_layers_hid_num):
            h = torch.sin(self.bra_fc[2*i](x))
            
            h = torch.sin(self.bra_fc[2*i+1](h))
            
            temp = torch.eye(x.shape[-1],self.bra_layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.bra_fc[-1](x)
    def trunk(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    
    def forward(self,data_u,x):
        bra = self.branch(data_u)
        tru = self.trunk(x)
        
        #print(bra.shape,tru.shape,(bra@tru.t()).shape)
        return bra@tru.t()
        
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])  
def pred_y(solvernet,x):#x = [fun_size,sample,3]
    return solvernet.forward(x)
#-----test
class Testdata():
    def __init__(self,fun_size,sample_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(sample_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_y = torch.zeros(fun_size,sample_size)
        self.data_u = torch.zeros(fun_size,sample_size)
        for i in range(fun_size):
            np.random.seed(seeds + i)
            torch.manual_seed(seeds + i)
            net_data = Net(layers,dtype)
            
            self.data_y[i:i + 1,:] = function_y(net_data,len_data,self.x).t()
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,self.x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample
def predata(data_u,data_y,data_x,solvernet,dev):
    data_u = torch.tensor(data_u).type(dtype)
    data_y = torch.tensor(data_y).type(dtype)
    data_x = torch.tensor(data_x).type(dtype)
    data_u = data_u.to(dev)
    data_y = data_y.to(dev)
    data_x = data_x.to(dev)
    solvernet = solvernet.to(dev)

data_size = data_y.shape[1]
input_dim = 2
output_dim = 9
layers = [15,15]
solvernet = Solvernet(data_size,input_dim,output_dim,layers, dtype)

#fname1 = "lay%d-ynet-var.pt"%(output_dim)
fname1 = ".//deeponet//lay%d-ynet-var.pt"%(output_dim)
#predata(data_u,data_y,data_x,solvernet,device)

solvernet = solvernet.to(device)
lr = 1e-1

solvernet = torch.load(fname1)
#-----test
class Testdata():
    def __init__(self,data_x,data_size,fun_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(data_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_y = torch.zeros(fun_size,data_size)
        self.data_u = torch.zeros(fun_size,data_x.shape[0])
        for i in range(fun_size):
            np.random.seed(seeds + i)
            torch.manual_seed(seeds + i)
            net_data = Net(layers,dtype)
            
            self.data_y[i:i + 1,:] = function_y(net_data,len_data,self.x).t()
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,data_x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample

test_size = 32*64
fun_size = 3
lay_wid = 20
testseeds = data_size
layers = [2,lay_wid,lay_wid,1]
data_x = torch.tensor(data_x).type(dtype)
test = Testdata(data_x,test_size,fun_size,layers,dtype,testseeds)
solvernet = solvernet.to('cpu')
print(solvernet)
y = solvernet.forward(test.data_u,test.x)
y_acc = test.data_y
err = (y - y_acc).reshape(-1,1)
L1 = max(abs(err))
L2 = (err**2).sum()
print('test error:L1:%.2e,L2:%.2e'%(L1,L2))

在这里插入图片描述

FNN.py

import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import time
from data import *
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#device = torch.device('cpu')
dtype = torch.float32

fname_y = "data_u.npy"
fname_u = "data_f.npy"
fname_x = "data_x.npy"

data_u = np.load(fname_y)#[fun_size,sample_size]
data_f = np.load(fname_u)#[fun_size,sample_size]
data_x = np.load(fname_x)#[sample_size,dim = 2]
def pre_data(data_f,data_u,data_x,dev):
    data_f = torch.tensor(data_f).type(dtype)
    data_u = torch.tensor(data_u).type(dtype)
    data_x = torch.tensor(data_x).type(dtype)
    fun_num = data_f.shape[0]
    input_x = data_x.repeat(fun_num,1,1)#[fun_size,sample_size,dim = 2]
    input_f = data_f.unsqueeze(2)#[fun_size,sample_size,1]
    input_u = data_u.unsqueeze(2)#[fun_size,sample_size,1]
    return torch.cat([input_f,input_x],dim = -1).to(dev),input_u.to(dev)#[fun_size,sample_size,dim = 3]和#[fun_size,sample_size,1]

class Solvernet(torch.nn.Module):
    def __init__(self, layers, dtype):
        super(Solvernet, self).__init__()
        self.layers = layers
        self.layers_hid_num = len(layers)-2
        self.device = device
        self.dtype = dtype
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
    def forward(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        return self.fc[-1](x) 

    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])
def pred_u(solvernet,x):#x = [fun_size,sample,3]
    return solvernet.forward(x)
def Loss(solvernet,x,data_u):
    u = pred_u(solvernet,x)
    err = ((u - data_u)**2).mean()
    return torch.sqrt(err)
def train_yp(solvernet,x,data_u,optim,scheduler,epoch,optimtype):
    print('Train y&p Neural Network')
    loss = Loss(solvernet,x,data_u)
    print('epoch:%d,loss:%.2e, time: %.2f'
          %(0, loss.item(), 0.00))
    for it in range(epoch):
        st = time.time()
        if optimtype == 'BFGS' or optimtype == 'LBFGS':
            def closure():
                optim.zero_grad()
                loss = Loss(solvernet,x,data_u)
                loss.backward()
                return loss
            optim.step(closure) 
        else:
            for j in range(100):
                optim.zero_grad()
                loss = Loss(solvernet,x,data_u)
                loss.backward()
                optim.step()
        scheduler.step()
        loss = Loss(solvernet,x,data_u)
        ela = time.time() - st
        print('epoch:%d,loss:%.2e, time: %.2f'
              %((it+1), loss.item(), ela))
x,data_u = pre_data(data_f,data_u,data_x,device)
width = 20
layers = [3,width,width,1]
solvernet = Solvernet(layers,dtype)
print('the total parameters:%d\n'%(solvernet.total_para()))
fname1 = "cnnlay%d-ynet-var.pt"%(width)
solvernet = solvernet.to(device)

lr = 1e0
#optimtype = 'Adam'
optimtype = 'BFGS'
if optimtype == 'BFGS':
    optim = torch.optim.LBFGS(solvernet.parameters(),
                      lr=lr, max_iter=100,
                      tolerance_grad=1e-16, tolerance_change=1e-16,
                      line_search_fn='strong_wolfe')
else:
    optim = torch.optim.Adam(solvernet.parameters(),
                      lr=lr,weight_decay=1e-4)    
step_size = 100
gamma = 0.5                     
scheduler = torch.optim.lr_scheduler.StepLR(optim, step_size=step_size, gamma=gamma)      

epoch = 1
#solvernet = torch.load(fname1)
train_yp(solvernet,x,data_u,optim,scheduler,epoch,optimtype)
torch.save(solvernet,fname1)
solvernet = torch.load(fname1)

#-----------------------
class Testdata():
    def __init__(self,fun_size,sample_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(sample_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_u = torch.zeros(fun_size,sample_size)
        self.data_f = torch.zeros(fun_size,sample_size)
        for i in range(fun_size):
            np.random.seed(seeds + i)
            torch.manual_seed(seeds + i)
            net_data = Net(layers,dtype)
            
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,self.x).t()
            self.data_f[i:i + 1,:] = function_f(net_data,len_data,self.x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample
layers = [2,lay_wid,lay_wid,lay_wid,1]

seeds = 10000
fun_size = 3
sample_size = 4000
teset = Testdata(fun_size,sample_size,layers,dtype,seeds)
data_f = teset.data_f.detach().numpy()
data_u = teset.data_u.detach().numpy()
data_x = teset.x.detach().numpy()
print(data_f.shape,data_u.shape,data_x.shape)
x,data_u = pre_data(data_f,data_u,data_x,device)
print(data_u.shape,x.shape)


y = pred_u(solvernet,x)
y_acc = data_u
err = (y - y_acc).reshape(-1,1)
L1 = max(abs(err))
L2 = (err**2).sum()
print('test error:L1:%.2e,L2:%.2e'%(L1,L2))

data_x的形状是[N,S,3],表示N个不同的右端项在S个不同的样本点的取值+坐标点，即data_x[k,S,0]表示第k个右端项在S个样本点的取值，data_x[N,S,1:3]表示S个样本点的坐标，也就是说data_x大部分内容都是一致的。
data_y形状是[N,S,1]，表示N个右端项在S个样本点对应的近似解标签，
经过模型G以后，输出的维度也是[N,S,1]表示模型G的预测。
后面的模型训练和测试集也是类似的，这里不介绍。

傅里叶神经网络FNO

参考文献：Fourier Neural Operator for Parametric Partial Dierential Equations
首先FNO接受的输入data_x的形状也是[N,S,3]，输出的形状也是[N,S,1]，这里说明，本人这里介绍的算法细节和论文不太一样，论文使用的样本点是N*N，表示的似乎是均匀剖分下的网格点，但是本人自己实现的时候使用的是随机采样，因此后面在定义网络的时候也有不同，FNO和上面这种做法最大的不同就在于网络的定义不一样。
1：先利用一层全连接，把输入维度从[N,S,3]提高到[N,S,width]，这个width后面可以自己设定。
2：定义一个傅里叶block，这里代码用SpectralConv2d表示，这个SpectralConv2d有三个参数，in_channel,out_channel,modes，后面我们实例化的时候一般定义的都是conv = SpectralConv2d(width,width,modes)
这里结合本人重点解读一下这个傅里叶block，SpectralConv2d
特别注意：X原来的形状是[N,S,width]，进入第一个傅里叶block之前，会对X做一个转置，X的形状会变成[N,width,S]。
在这里插入图片描述
首先定义两个三维的权重矩阵w1 = [in_channels,out_channels,modes],w2 = [in_channels,out_channels,modes]
48行这个函数其实是在做矩阵的乘法，爱因斯坦求和，先解释一下爱因斯坦求和torch.einsum(“bix,iox->box”, input, weights)
假设输入input = [N,width,M],权重weight = [width,height,M]，那么torch.einsum(“bix,iox->box”, input, weights)表示前面两个维度做矩阵乘法，也就是说输出的形状应该是[N,height,M]。
54行代码会把X的形状由[N,width,S]变成[N,width,S//2 + 1]，而58行和59行分别利用到第3个维度的前面modes和后面modes行的数据，因此modes一定要小于S//2 + 1
所以这个forward函数是这样工作的，接受的输入x=[N,width,S]
54行得到的x_ft = [N,width,S//2 + 1]
58，59行利用爱因斯坦求和对x_ft的两部分做一个矩阵乘积以后重新组合得到的out_ft形状=[N,width,S//2 +1]，
61行经过傅里叶逆变换以后x的形状恢复为[N,width,S]，有了这个理解以后，下面我们看一看这个求解器具体的定义如何，参考代码如下：

class Solvernet(torch.nn.Module):
    def __init__(self, width,modes):
        super(Solvernet, self).__init__()
        self.modes = modes
        
        self.width = width
        
        self.fc0 = nn.Linear(3, self.width) # input channel is 3: (a(x, y), x, y)
        self.conv0 = SpectralConv2d(self.width, self.width, self.modes)
        self.conv1 = SpectralConv2d(self.width, self.width, self.modes)
        self.conv2 = SpectralConv2d(self.width, self.width, self.modes)
        
        self.w0 = nn.Conv1d(self.width, self.width, 1)
        self.w1 = nn.Conv1d(self.width, self.width, 1)
        self.w2 = nn.Conv1d(self.width, self.width, 1)
        

        self.fc1 = nn.Linear(self.width, 16)
        self.fc2 = nn.Linear(16, 1)
    def forward(self, x):
        
        x = self.fc0(x)#[fun_num,sample_num,width]
        x = x.permute(0,2,1)
        #x = F.gelu(x)
        x1 = self.conv0(x)
        x2 = self.w0(x)
        x = x1 + x2
        x = F.gelu(x)

        x1 = self.conv1(x)
        x2 = self.w1(x)
        x = x1 + x2
        x = F.gelu(x)

        x1 = self.conv2(x)
        x2 = self.w2(x)
        x = x1 + x2
        x = F.gelu(x)
        
        x = x.permute(0, 2, 1)
        x = self.fc1(x)
        x = F.gelu(x)
        x = self.fc2(x)
        return x
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])

值得注意的是这个求解器里面定义的一维卷积w0,w1,w2，以w0为例子，w0接受的输入也是[N,width,S]，输出的形状仍然是[N,width,S]，在文章里面有下面这个公式，在代码里面的实现其实就是conv(x) + w(x)，只不过这里的矩阵乘法用的是一维卷积代替而已。
在这里插入图片描述
这个算法本人实现的并不好，本人做了数值实验以后发现损失函数下降特别慢，泛化能力也很差。这个文章本人一开始阅读觉得特别难以理解的部分其实是傅里叶block的解读，尤其是里面的形状变化，这个傅里叶block文章解释的意思是说想要模拟格林函数，但是这个不知道是否可以站住脚。
最后需要指出：本人实现的这几个代码由于一直没有学会文章中的那个高斯采样方法，所以右端项只好使用不同的随机种子播撒出不同的神经网络，因此对于右端项(非神经网络构造)的泛化能力很有可能会极差，另一方面，该文章使用的标签是通过高精度求解器获得的，本人使用反向传播得到的标签，整个过程简化如下：
播撒随机种子，得到不同的FNN Net——>反向传播得到右端项u
区域内撒点——>得到样本点，整合得到(u,x,y)作为输入
构造模型——>得到近似解y,
通过播撒随机种子得到不同的测试集u，
FFTsolver.py

import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import time
from data import *
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#device = torch.device('cpu')
dtype = torch.float32

fname_y = "data_u.npy"
fname_u = "data_f.npy"
fname_x = "data_x.npy"


data_u = np.load(fname_y)#[fun_size,sample_size]
data_f = np.load(fname_u)#[fun_size,sample_size]
data_x = np.load(fname_x)#[sample_size,dim = 2]
def pre_data(data_f,data_u,data_x,dev):
    data_f = torch.tensor(data_f).type(dtype)
    data_u = torch.tensor(data_u).type(dtype)
    data_x = torch.tensor(data_x).type(dtype)
    fun_num = data_f.shape[0]
    input_x = data_x.repeat(fun_num,1,1)#[fun_size,sample_size,dim = 2]
    input_f = data_f.unsqueeze(2)#[fun_size,sample_size,1]
    input_u = data_u.unsqueeze(2)#[fun_size,sample_size,1]
    return torch.cat([input_f,input_x],dim = -1).to(dev),input_u.to(dev)#[fun_size,sample_size,dim = 3]和#[fun_size,sample_size,1]
class SpectralConv2d(torch.nn.Module):
    def __init__(self, in_channels, out_channels, modes):
        super(SpectralConv2d, self).__init__()
        """
        2D Fourier layer. It does FFT, linear transform, and Inverse FFT.    
        """
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.modes = modes #Number of Fourier modes to multiply, at most floor(N/2) + 1
        
        self.scale = (1 / (in_channels * out_channels))
        self.weights1 = nn.Parameter(self.scale * torch.rand(in_channels, out_channels, self.modes, dtype=torch.cfloat))
        self.weights2 = nn.Parameter(self.scale * torch.rand(in_channels, out_channels, self.modes,  dtype=torch.cfloat))
        #in_channels，out_channals对应的是空间维度，后面会把维度=3提升到dim = width
        #modes对应的是样本点数目，后面会根据modes把样本点分成两份，分别做矩阵乘积
    # Complex multiplication
    def compl_mul2d(self, input, weights):
        #input = (fun_num,input_size,sample_size),weight = (input_size,out_size,sample_size)->(fun_num,out_size,sample_size)
        #爱因斯坦求和，这里把数组前面两个维度做了一个矩阵乘
        return torch.einsum("bix,iox->box", input, weights)
    def forward(self, x):
        #x = [fun_size,width,sample_size]
        x_ft = torch.fft.rfft2(x)#x_ft = [fun_size,width,sample_size//2 + 1]
        # Multiply relevant Fourier modes
        out_ft = torch.zeros_like(x_ft)
        #特别注意，这里的modes一定要小于sample_size//2 + 1
        out_ft[:, :, :self.modes] = self.compl_mul2d(x_ft[:, :, :self.modes], self.weights1)
        out_ft[:, :, -self.modes:] = self.compl_mul2d(x_ft[:, :, -self.modes:], self.weights2)
        #Return to physical space
        x = torch.fft.irfft2(out_ft, s=(x.size(-2), x.size(-1)))
        #此时的x形状和一开始一样，也是[fun_size,width,sample_size]
        return x
class Solvernet(torch.nn.Module):
    def __init__(self, width,modes):
        super(Solvernet, self).__init__()
        self.modes = modes
        
        self.width = width
        
        self.fc0 = nn.Linear(3, self.width) # input channel is 3: (a(x, y), x, y)
        self.conv0 = SpectralConv2d(self.width, self.width, self.modes)
        self.conv1 = SpectralConv2d(self.width, self.width, self.modes)
        self.conv2 = SpectralConv2d(self.width, self.width, self.modes)
        
        self.w0 = nn.Conv1d(self.width, self.width, 1)
        self.w1 = nn.Conv1d(self.width, self.width, 1)
        self.w2 = nn.Conv1d(self.width, self.width, 1)
        

        self.fc1 = nn.Linear(self.width, 16)
        self.fc2 = nn.Linear(16, 1)
    def forward(self, x):
        
        x = self.fc0(x)#[fun_num,sample_num,width]
        x = x.permute(0,2,1)
        #x = F.gelu(x)
        x1 = self.conv0(x)
        x2 = self.w0(x)
        x = x1 + x2
        x = F.gelu(x)

        x1 = self.conv1(x)
        x2 = self.w1(x)
        x = x1 + x2
        x = F.gelu(x)

        x1 = self.conv2(x)
        x2 = self.w2(x)
        x = x1 + x2
        x = F.gelu(x)
        
        x = x.permute(0, 2, 1)
        x = self.fc1(x)
        x = F.gelu(x)
        x = self.fc2(x)
        return x
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])
def pred_u(solvernet,x):#x = [fun_size,sample,3]
    return solvernet.forward(x)
def Loss(solvernet,x,data_u):
    y = pred_u(solvernet,x)
    err = ((y - data_u)**2).mean()
    return torch.sqrt(err)
def train_yp(solvernet,x,data_u,optim,scheduler,epoch,optimtype):
    print('Train y&p Neural Network')
    loss = Loss(solvernet,x,data_u)
    print('epoch:%d,loss:%.2e, time: %.2f'
          %(0, loss.item(), 0.00))
    for it in range(epoch):
        st = time.time()
        if optimtype == 'BFGS' or optimtype == 'LBFGS':
            def closure():
                optim.zero_grad()
                loss = Loss(solvernet,x,data_u)
                loss.backward()
                return loss
            optim.step(closure) 
        else:
            for j in range(100):
                optim.zero_grad()
                loss = Loss(solvernet,x,data_u)
                loss.backward()
                optim.step()
        scheduler.step()
        loss = Loss(solvernet,x,data_u)
        ela = time.time() - st
        print('epoch:%d,loss:%.2e, time: %.2f'
              %((it+1), loss.item(), ela))
x,data_u = pre_data(data_f,data_u,data_x,device)
width = 10
modes = data_x.shape[1]//4 + 1
solvernet = Solvernet(width,modes)
fname1 = "fftlay%d-ynet-var.pt"%(width)
solvernet = solvernet.to(device)
lr = 1e0
optimtype = 'Adam'
#optimtype = 'BFGS'
if optimtype == 'BFGS':
    optim = torch.optim.LBFGS(solvernet.parameters(),
                      lr=lr, max_iter=100,
                      tolerance_grad=1e-16, tolerance_change=1e-16,
                      line_search_fn='strong_wolfe')
else:
    optim = torch.optim.Adam(solvernet.parameters(),
                      lr=lr,weight_decay=1e-4)    
step_size = 100
gamma = 0.5                     
scheduler = torch.optim.lr_scheduler.StepLR(optim, step_size=step_size, gamma=gamma)      

epoch = 1
#solvernet = torch.load(fname1)
print(x.shape,data_u.shape)
#train_yp(solvernet,x,data_u,optim,scheduler,epoch,optimtype)
torch.save(solvernet,fname1)
solvernet = torch.load(fname1)

#-----------------------
class Testdata():
    def __init__(self,fun_size,sample_size,layers,dtype,seeds):
        self.dim = 2
        tmp = self.quasi_samples(sample_size)
        tmp[:,0] = tmp[:,0]*(bound[0,1] - bound[0,0]) + bound[0,0]
        tmp[:,1] = tmp[:,1]*(bound[1,1] - bound[1,0]) + bound[1,0]
        self.x = torch.tensor(tmp).type(dtype)
        self.data_u = torch.zeros(fun_size,sample_size)
        self.data_f = torch.zeros(fun_size,sample_size)
        for i in range(fun_size):
            np.random.seed(seeds + i)
            torch.manual_seed(seeds + i)
            net_data = Net(layers,dtype)
            
            self.data_u[i:i + 1,:] = function_u(net_data,len_data,self.x).t()
            self.data_f[i:i + 1,:] = function_f(net_data,len_data,self.x).t()
    def quasi_samples(self,N):
        sampler = qmc.Sobol(d=self.dim)
        sample = sampler.random(n=N)
        return sample
layers = [2,lay_wid,lay_wid,lay_wid,1]

seeds = 10000
fun_size = 3
sample_size = 4000
teset = Testdata(fun_size,sample_size,layers,dtype,seeds)
data_f = teset.data_f.detach().numpy()
data_u = teset.data_u.detach().numpy()
data_x = teset.x.detach().numpy()
print(data_f.shape,data_u.shape,data_x.shape)
x,data_u = pre_data(data_f,data_u,data_x,device)
print(data_u.shape,x.shape)


y = pred_u(solvernet,x)
y_acc = data_u
err = (y - y_acc).reshape(-1,1)
L1 = max(abs(err))
L2 = (err**2).sum()
print('test error:L1:%.2e,L2:%.2e'%(L1,L2))

差分法和DeepOnet结合

import numpy as np
import torch
import torch.nn as nn
import time
import matplotlib.pyplot as plt
from scipy.stats import qmc
import itertools
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#device = torch.device('cpu')
dtype = torch.float32

mu1 = 2
mu2 = 0.6
hr = 0
bound = np.array([0 + hr,1 + mu1 - hr,0 + hr,1 - hr]).reshape(2,2)
def UU(X, order,prob):#X表示(x,t)
    if prob==1:
        temp = 10*(X[:,0]+X[:,1])**2 + (X[:,0]-X[:,1])**2 + 0.5
        if order[0]==0 and order[1]==0:
            return torch.log(temp)
        if order[0]==1 and order[1]==0:#对x求偏导
            return temp**(-1) * (20*(X[:,0]+X[:,1]) + 2*(X[:,0]-X[:,1]))
        if order[0]==0 and order[1]==1:#对t求偏导
            return temp**(-1) * (20*(X[:,0]+X[:,1]) - 2*(X[:,0]-X[:,1]))
        if order[0]==2 and order[1]==0:
            return - temp**(-2) * (20*(X[:,0]+X[:,1])+2*(X[:,0]-X[:,1])) ** 2 \
                   + temp**(-1) * (22)
        if order[0]==1 and order[1]==1:
            return - temp**(-2) * (20*(X[:,0]+X[:,1])+2*(X[:,0]-X[:,1])) \
                   * (20*(X[:,0]+X[:,1])-2*(X[:,0]-X[:,1])) \
                   + temp**(-1) * (18)
        if order[0]==0 and order[1]==2:
            return - temp**(-2) * (20*(X[:,0]+X[:,1])-2*(X[:,0]-X[:,1])) ** 2 \
                   + temp**(-1) * (22)
    if prob==2:
        if order[0]==0 and order[1]==0:
            return (X[:,0]*X[:,0]*X[:,0]-X[:,0]) * \
                   0.5*(torch.exp(2*X[:,1])+torch.exp(-2*X[:,1]))
        if order[0]==1 and order[1]==0:
            return (3*X[:,0]*X[:,0]-1) * \
                   0.5*(torch.exp(2*X[:,1])+torch.exp(-2*X[:,1]))
        if order[0]==0 and order[1]==1:
            return (X[:,0]*X[:,0]*X[:,0]-X[:,0]) * \
                   (torch.exp(2*X[:,1])-torch.exp(-2*X[:,1]))
        if order[0]==2 and order[1]==0:
            return (6*X[:,0]) * \
                   0.5*(torch.exp(2*X[:,1])+torch.exp(-2*X[:,1]))
        if order[0]==1 and order[1]==1:
            return (3*X[:,0]*X[:,0]-1) * \
                   (torch.exp(2*X[:,1])-torch.exp(-2*X[:,1]))
        if order[0]==0 and order[1]==2:
            return (X[:,0]*X[:,0]*X[:,0]-X[:,0]) * \
                   2*(torch.exp(2*X[:,1])+torch.exp(-2*X[:,1]))
    if prob==3:
        temp1 = X[:,0]*X[:,0] - X[:,1]*X[:,1]
        temp2 = X[:,0]*X[:,0] + X[:,1]*X[:,1] + 0.1
        if order[0]==0 and order[1]==0:
            return temp1 * temp2**(-1)
        if order[0]==1 and order[1]==0:
            return (2*X[:,0]) * temp2**(-1) + \
                   temp1 * (-1)*temp2**(-2) * (2*X[:,0])
        if order[0]==0 and order[1]==1:
            return (-2*X[:,1]) * temp2**(-1) + \
                   temp1 * (-1)*temp2**(-2) * (2*X[:,1])
        if order[0]==2 and order[1]==0:
            return (2) * temp2**(-1) + \
                   2 * (2*X[:,0]) * (-1)*temp2**(-2) * (2*X[:,0]) + \
                   temp1 * (2)*temp2**(-3) * (2*X[:,0])**2 + \
                   temp1 * (-1)*temp2**(-2) * (2)
        if order[0]==1 and order[1]==1:
            return (2*X[:,0]) * (-1)*temp2**(-2) * (2*X[:,1]) + \
                   (-2*X[:,1]) * (-1)*temp2**(-2) * (2*X[:,0]) + \
                   temp1 * (2)*temp2**(-3) * (2*X[:,0]) * (2*X[:,1])
        if order[0]==0 and order[1]==2:
            return (-2) * temp2**(-1) + \
                   2 * (-2*X[:,1]) * (-1)*temp2**(-2) * (2*X[:,1]) + \
                   temp1 * (2)*temp2**(-3) * (2*X[:,1])**2 + \
                   temp1 * (-1)*temp2**(-2) * (2)

class Net(torch.nn.Module):
    def __init__(self, layers, dtype):
        super(Net, self).__init__()
        self.layers = layers
        self.layers_hid_num = len(layers)-2
        
        self.dtype = dtype
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
    def forward(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])                    
class LEN():
    def __init__(self):
        pass
    def forward(self,x):
        
        x1 = x[:,0:1]
        x2 = x[:,1:2]
        L = (x1 - bound[0,0])*(bound[0,1] - x1)*(x2 - bound[1,0])*(bound[1,1] - x2)
        return L.reshape(-1,1)
len_data = LEN()
def bd_y(x):
    return torch.ones_like(x[:,0:1])
def function_u(prob,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    return UU(x,[0,0],prob).reshape(-1,1)*len_data.forward(x) + bd_y(x)
def function_f(prob,len_data,x):
    if x.requires_grad == False:
        x.requires_grad = True
    state = function_u(prob,len_data,x)
    #print(state.shape,x.shape)
    state_x, = torch.autograd.grad(state,x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))
    state_xx, = torch.autograd.grad(state_x[:,0:1],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1])) 
    state_yy, = torch.autograd.grad(state_x[:,1:2],x, create_graph=True, retain_graph=True,
                               grad_outputs=torch.ones_like(x[:,0:1]))     
    state_lap = state_xx[:,0:1] + state_yy[:,1:2]
    x.requires_grad = False
    return -state_lap.data 
np.random.seed(1234)
torch.manual_seed(1234)
class FD():
    def __init__(self,bound,nx,fun_size,layers,dtype,seeds):
        self.hx = [(bound[0,1] - bound[0,0])/(nx[0] - 1),(bound[1,1] - bound[1,0])/(nx[1] - 1)]
        self.X = torch.zeros(nx[0]*nx[1],2)
        for j in range(nx[1]):
            for i in range(nx[0]):
                self.X[j*nx[0] + i,0] = bound[0,0] + i*self.hx[0]
                self.X[j*nx[0] + i,1] = bound[1,0] + j*self.hx[1]
        self.nx = nx
        self.rig = torch.zeros(fun_size,nx[0]*nx[1])
        for i in range(fun_size):
            np.random.seed(seeds + 10*i)
            torch.manual_seed(seeds + 10*i)
            net_data = Net(layers,dtype)
            #print(self.rig[i:i+1,:].shape,net_data.forward(self.X).shape)
            self.rig[i:i + 1,:] = net_data.forward(self.X).t()
        for i in range(3):
            self.rig[i:i + 1,:] = function_f(i + 1,len_data,self.X).t()
        self.data_x = self.X.detach().numpy()
        self.data_f = self.rig.detach().numpy()
        #print(self.data_f.shape)
        self.data_u = self.allsolve(self.data_f)
        for i in range(3):
            #print(self.data_u[i:i + 1,:].shape,function_u(i + 1,len_data,self.X).shape)
            err = self.data_u[i:i + 1,:].T - function_u(i + 1,len_data,self.X).detach().numpy()
            print(max(abs(err)))
    def matrix(self):
        A = np.zeros([self.nx[0]*self.nx[1],self.nx[0]*self.nx[1]])
        for j in range(self.nx[1]):
            for i in range(self.nx[0]):
                if i == 0 or i == self.nx[0] - 1 or j == 0 or j == self.nx[1] - 1:
                    A[j*self.nx[0] + i,j*self.nx[0] + i] = 1
                
                else:
                    A[j*self.nx[0] + i,j*self.nx[0] + i] = 2*(self.hx[0]/self.hx[1] + self.hx[1]/self.hx[0])
                    A[j*self.nx[0] + i,(j - 1)*self.nx[0] + i] = -self.hx[0]/self.hx[1]
                    A[j*self.nx[0] + i,(j + 1)*self.nx[0] + i] = -self.hx[0]/self.hx[1]
                    A[j*self.nx[0] + i,j*self.nx[0] + i - 1] = - self.hx[1]/self.hx[0]
                    A[j*self.nx[0] + i,j*self.nx[0] + i + 1] = - self.hx[1]/self.hx[0]
        return A
    def right(self,rig):
        b = np.zeros([self.nx[0]*self.nx[1],1])
        for j in range(self.nx[1]):
            for i in range(self.nx[0]):
                x = self.X[j*self.nx[0] + i:j*self.nx[0] + i + 1,:]
                if i == 0 or i == self.nx[0] - 1 or j == 0 or j == self.nx[1] - 1:
                    b[j*self.nx[0] + i,0] = bd_y(x)
                else:
                    b[j*self.nx[0] + i,0] =  rig[:,j*self.nx[0] + i]*self.hx[0]*self.hx[1]
        return b
    def allsolve(self,rig):#第0个维度放数值，第1个维度放数量
        u = np.zeros([rig.shape[0],self.nx[0]*self.nx[1]])
        A = self.matrix()
        for i in range(rig.shape[0]):
            b = self.right(rig[i:i + 1])
            tmp = np.linalg.solve(A,b)
            #print(b.shape,tmp.shape)
            u[i:i + 1,:] = tmp.T
        return u
def error(u_pred,u_acc):
    temp = ((u_pred - u_acc)**2).sum()/(u_acc**2).sum()
    return temp**(0.5)
nx = [32,32]
fun_size = 1000
lay_wid = 20
layers = [2,lay_wid,lay_wid,lay_wid,1]
dtype = torch.float32
seeds = 0
fd = FD(bound,nx,fun_size,layers,dtype,seeds)
output_dim = 9

np.save('fddata_u.npy',fd.data_u)
np.save('fddata_f.npy',fd.data_f)
np.save('fddata_x.npy',fd.data_x)
fname_u = "fddata_u.npy"
fname_x = "fddata_x.npy"
fname_f = "fddata_f.npy"
fname1 = "fdlay%d-ynet-var.pt"%(output_dim)

'''
np.save('C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_u.npy',fd.data_u)
np.save('C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_f.npy',fd.data_f)
np.save('C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_x.npy',fd.data_x)
#%%
fname_u = "C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_u.npy"
fname_x = "C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_x.npy"
fname_f = "C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fddata_f.npy"
fname1 = "C://Users//2001213226//Desktop//graduation//OCPnet//nobox//fdlay%d-ynet-var.pt"%(output_dim)
'''
data_u = np.load(fname_u)
data_f = np.load(fname_f)
data_x = np.load(fname_x)
#%%
class Solvernet(torch.nn.Module):
    def __init__(self, data_size,input_dim,output_dim,layers, dtype):#注意这里的layers只是hidden
        super(Solvernet, self).__init__()
        
        
        self.dtype = dtype
        #------------------------
        self.kernel_size = [10,6,10]
        self.stride = [1,2,2]
        cov = []
        out_dim = [3,1,1]
        in_dim = 1

        for i in range(len(self.kernel_size)):
            cov.append(nn.Conv1d(in_channels = in_dim,out_channels = out_dim[i],kernel_size = self.kernel_size[i],stride = self.stride[i]))
            data_size = (data_size - self.kernel_size[i])//self.stride[i] + 1
            in_dim = out_dim[i]
        self.cov = torch.nn.Sequential(*cov)
        for i in range(len(self.kernel_size)):
            self.cov[i].weight.data = self.cov[i].weight.data.type(dtype)
            self.cov[i].bias.data = self.cov[i].bias.data.type(dtype)
        #------------------------
        #-------branch DNN
        self.bra_layers = [data_size] + layers + [output_dim]
        
        self.bra_layers_hid_num = len(self.bra_layers)-2
        bra_fc = []
        for i in range(self.bra_layers_hid_num+1):
            bra_fc.append(torch.nn.Linear(self.bra_layers[i],self.bra_layers[i+1]))
            bra_fc.append(torch.nn.Linear(self.bra_layers[i + 1],self.bra_layers[i+1]))
        bra_fc.append(torch.nn.Linear(self.bra_layers[-2],self.bra_layers[-1]))
        self.bra_fc = torch.nn.Sequential(*bra_fc)
        for i in range(self.bra_layers_hid_num+1):
            self.bra_fc[2*i].weight.data = self.bra_fc[2*i].weight.data.type(dtype)
            self.bra_fc[2*i].bias.data = self.bra_fc[2*i].bias.data.type(dtype)
            self.bra_fc[2*i + 1].weight.data = self.bra_fc[2*i + 1].weight.data.type(dtype)
            self.bra_fc[2*i + 1].bias.data = self.bra_fc[2*i + 1].bias.data.type(dtype)
        self.bra_fc[-1].weight.data = self.bra_fc[-1].weight.data.type(dtype)
        self.bra_fc[-1].bias.data = self.bra_fc[-1].bias.data.type(dtype)
        #------------------------
        self.layers = [input_dim] + layers + [output_dim]
        self.layers_hid_num = len(self.layers)-2
        fc = []
        for i in range(self.layers_hid_num):
            fc.append(torch.nn.Linear(self.layers[i],self.layers[i+1]))
            fc.append(torch.nn.Linear(self.layers[i+1],self.layers[i+1]))
        fc.append(torch.nn.Linear(self.layers[-2],self.layers[-1]))
        self.fc = torch.nn.Sequential(*fc)
        for i in range(self.layers_hid_num):
            self.fc[2*i].weight.data = self.fc[2*i].weight.data.type(dtype)
            self.fc[2*i].bias.data = self.fc[2*i].bias.data.type(dtype)
            self.fc[2*i + 1].weight.data = self.fc[2*i + 1].weight.data.type(dtype)
            self.fc[2*i + 1].bias.data = self.fc[2*i + 1].bias.data.type(dtype)
        self.fc[-1].weight.data = self.fc[-1].weight.data.type(dtype)
        self.fc[-1].bias.data = self.fc[-1].bias.data.type(dtype)
        
    def CNN(self,x):
        h = x.reshape(x.shape[0],1,x.shape[1])
        for i in range(len(self.cov)):
            h = self.cov[i](h)
            h = torch.sin(h)
        #print(h.shape)
        return h.squeeze(dim = 1)
    def branch(self,data_f):
        
        x = self.CNN(data_f)
        dev = x.device
        for i in range(self.bra_layers_hid_num):
            h = torch.sin(self.bra_fc[2*i](x))
            
            h = torch.sin(self.bra_fc[2*i+1](h))
            
            temp = torch.eye(x.shape[-1],self.bra_layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.bra_fc[-1](x)
    def trunk(self, x):
        dev = x.device
        for i in range(self.layers_hid_num):
            h = torch.sin(self.fc[2*i](x))
            h = torch.sin(self.fc[2*i+1](h))
            temp = torch.eye(x.shape[-1],self.layers[i+1],dtype = self.dtype,device = dev)
            x = h + x@temp
        
        return self.fc[-1](x)
    
    def forward(self,data_f,x):
        bra = self.branch(data_f)
        tru = self.trunk(x)
        
        #print(bra.shape,tru.shape,(bra@tru.t()).shape)
        return bra@tru.t()
    def backward(self,data_f,x):
        if data_f.requires_grad == False:
            data_f.requires_grad = True
        bra = self.branch(data_f)
        
        bra_u = torch.zeros(data_f.shape[1],bra.shape[1])
        for i in range(bra_u.shape[1]):
            tmp, = torch.autograd.grad(bra[:,i:i + 1], data_f, create_graph=True, retain_graph=True,
                                   grad_outputs=torch.ones(data_f.shape[0],1))
            bra_u[:,i:i + 1] = tmp.t()
        tru = self.trunk(x)
        
        return bra_u@tru.t()
    def total_para(self):#计算参数数目
        return sum([x.numel() for x in self.parameters()])
def pred_u(solvernet,data_f,x):
    return solvernet.forward(data_f,x)
def Loss(solvernet,data_f,x,data_u):
    y = pred_u(solvernet,data_f,x)
    err = ((y - data_u)**2).sum()
    return torch.sqrt(err)
def train_yp(solvernet,data_f,x,data_u,optim,epoch):
    print('Train y&p Neural Network')
    loss = Loss(solvernet,data_f,x,data_u)
    print('epoch:%d,loss:%.2e, time: %.2f'
          %(0, loss.item(), 0.00))
    for it in range(epoch):
        st = time.time()
        def closure():
            loss = Loss(solvernet,data_f,x,data_u)
            optim.zero_grad()
            loss.backward()
            return loss
        optim.step(closure) 
        loss = Loss(solvernet,data_f,x,data_u)
        ela = time.time() - st
        print('epoch:%d,loss:%.2e, time: %.2f'
              %((it+1), loss.item(), ela))
data_f = torch.tensor(data_f).type(dtype)
data_u = torch.tensor(data_u).type(dtype)
data_x = torch.tensor(data_x).type(dtype)
data_f = data_f.to(device)
data_u = data_u.to(device)
data_x = data_x.to(device)
data_size = data_u.shape[1]
input_dim = 2

layers = [15,15]
solvernet = Solvernet(data_size,input_dim,output_dim,layers, dtype)

solvernet = solvernet.to(device)
lr = 1e-1
optim = torch.optim.LBFGS(solvernet.parameters(),
                      lr=lr, max_iter=100,
                      tolerance_grad=1e-16, tolerance_change=1e-16,
                      line_search_fn='strong_wolfe')
epoch = 1
y = solvernet.forward(data_f,data_x)
train_yp(solvernet,data_f,data_x,data_u,optim,epoch)
torch.save(solvernet,fname1)
solvernet = torch.load(fname1)
#%%
device = 'cpu'
lay_wid = 20
layers = [2,lay_wid,lay_wid,lay_wid,1]
netu = Net(layers,dtype).to(device)
data_x = data_x.to(device)
solvernet = solvernet.to(device)
def pred_f(netu,x):
    return netu.forward(x)
class FENET():
    def __init__(self,bounds,nx):
        self.dim = 2
        self.bounds = bounds
        self.hx = [(bounds[0,1] - bounds[0,0])/nx[0],
                  (bounds[1,1] - bounds[1,0])/nx[1]]
        self.nx = nx
        self.gp_num = 2
        self.gp_pos = [(1 - np.sqrt(3)/3)/2,(1 + np.sqrt(3)/3)/2]
        self.Node()
        self.Unit()
        
    def Node(self):#生成网格点(M + 1)*(N + 1)
        self.Nodes_size = (self.nx[0] + 1)*(self.nx[1] + 1)
        self.Nodes = np.zeros([self.Nodes_size,self.dim])
        m = 0
        for i in range(self.nx[0] + 1):
            for j in range(self.nx[1] + 1):
                self.Nodes[m,0] = self.bounds[0,0] + i*self.hx[0]
                self.Nodes[m,1] = self.bounds[1,0] + j*self.hx[1]
                m = m + 1
    def phi(self,X,order):#[-1,1]*[-1,1]，在原点取值为1，其他网格点取值为0的基函数
        ind00 = (X[:,0] >= -1);ind01 = (X[:,0] >= 0);ind02 = (X[:,0] >= 1)
        ind10 = (X[:,1] >= -1);ind11 = (X[:,1] >= 0);ind12 = (X[:,1] >= 1)
        if order == [0,0]:
            return (ind00*~ind01*ind10*~ind11).astype('float32')*(1 + X[:,0])*(1 + X[:,1]) + \
                    (ind01*~ind02*ind10*~ind11).astype('float32')*(1 - X[:,0])*(1 + X[:,1]) + \
                    (ind00*~ind01*ind11*~ind12).astype('float32')*(1 + X[:,0])*(1 - X[:,1]) + \
                    (ind01*~ind02*ind11*~ind12).astype('float32')*(1 - X[:,0])*(1 - X[:,1])
        if order == [1,0]:
            return (ind00*~ind01*ind10*~ind11).astype('float32')*(1 + X[:,1]) + \
                    (ind01*~ind02*ind10*~ind11).astype('float32')*(-(1 + X[:,1])) + \
                    (ind00*~ind01*ind11*~ind12).astype('float32')*(1 - X[:,1]) + \
                    (ind01*~ind02*ind11*~ind12).astype('float32')*(-(1 - X[:,1]))
        if order == [0,1]:
            return (ind00*~ind01*ind10*~ind11).astype('float32')*(1 + X[:,0]) + \
                    (ind01*~ind02*ind10*~ind11).astype('float32')*(1 - X[:,0]) + \
                    (ind00*~ind01*ind11*~ind12).astype('float32')*(-(1 + X[:,0])) + \
                    (ind01*~ind02*ind11*~ind12).astype('float32')*(-(1 - X[:,0]))
    def basic(self,X,order,i):#根据网格点的存储顺序，遍历所有网格点，取基函数
        temp = (X - self.Nodes[i,:])/np.array([self.hx[0],self.hx[1]])
        if order == [0,0]:
            return self.phi(temp,order)
        if order == [1,0]:
            return self.phi(temp,order)/self.hx[0]
        if order == [0,1]:
            return self.phi(temp,order)/self.hx[1]
    def Unit(self):#生成所有单元，单元数目(M*N)
        self.Units_size = self.nx[0]*self.nx[1]
        self.Units_Nodes = np.zeros([self.Units_size,4],np.int32)#每个单元有4个点，记录这4个点的整体编号
        self.Units_Int_Points = np.zeros([self.Units_size,#划分成M*N个小区域，每个区域有4个高斯积分点
                                          self.gp_num*self.gp_num,self.dim])
        
        m = 0
        for i in range(self.nx[0]):
            for j in range(self.nx[1]):
                self.Units_Nodes[m,0] = i*(self.nx[1] + 1) + j
                self.Units_Nodes[m,1] = i*(self.nx[1] + 1) + j + 1
                self.Units_Nodes[m,2] = (i + 1)*(self.nx[1] + 1) + j
                self.Units_Nodes[m,3] = (i + 1)*(self.nx[1] + 1) + j + 1
                n = 0
                for k in range(self.gp_num):
                    for l in range(self.gp_num):
                        self.Units_Int_Points[m,n,0] = \
                            self.bounds[0,0] + (i + self.gp_pos[k])*self.hx[0]
                        self.Units_Int_Points[m,n,1] = \
                            self.bounds[1,0] + (j + self.gp_pos[l])*self.hx[1]
                        n = n + 1
                m = m + 1
        
    def Int_basic_basic(self,i,j,u_ind):#表示第i,j个基函数的梯度的乘积，以及在第u_ind个区域的积分
        X = self.Units_Int_Points[u_ind,:,:]#[4,2]
        basic0 = np.zeros_like(X)
        basic0[:,0] = self.basic(X,[1,0],i)
        basic0[:,1] = self.basic(X,[0,1],i)
        
        basic1 = np.zeros_like(X)
        basic1[:,0] = self.basic(X,[1,0],j)
        basic1[:,1] = self.basic(X,[0,1],j)
        return ((basic0*basic1).sum(1)).mean()*self.hx[0]*self.hx[1]
    def Int_F_basic(self,i,u_ind):#第i个基函数与右端项乘积，在第u_ind个单元积分
        X = self.Units_Int_Points[u_ind,:,:]
        x_net = torch.tensor(X).type(dtype)
        return (pred_f(netu,x_net).detach().numpy()*self.basic(X,[0,0],i)).mean()*self.hx[0]*self.hx[1]
    
    def matrix(self):
        A = np.zeros([self.Nodes_size,self.Nodes_size])#self.Nodes_size = (M+ 1)*(N + 1)
        for m in range(self.Units_size):#self.Units_size = M*N，第m个区域单元的4个积分点
            for k in range(4):
                ind0 = self.Units_Nodes[m,k]#self.Units_Nodes = [M*N,4],第m个区域中第k个网格点，第k个基函数编号
                for l in range(4):
                    ind1 = self.Units_Nodes[m,l]#self.Units_Nodes = [M*N,4],第m个区域中第l网格点，第k个基函数编号
                    #第m个区域上，两个基函数梯度的乘积的积分a(u,v)
                    A[ind0,ind1] += self.Int_basic_basic(ind0,ind1,m)
        
        for i in range(self.nx[0] + 1):
            ind = i*(self.nx[1] + 1)
            A[ind,:] = np.zeros([1,self.Nodes_size])
            A[ind,ind] = 1.0
            ind = (i + 1)*(self.nx[1] + 1) - 1
            A[ind,:] = np.zeros([1,self.Nodes_size])
            A[ind,ind] = 1.0
        for j in range(1,self.nx[1]):
            ind = j
            A[ind,:] = np.zeros([1,self.Nodes_size])
            A[ind,ind] = 1.0
            ind  = self.nx[0]*(self.nx[1] + 1) + j
            A[ind,:] = np.zeros([1,self.Nodes_size])
            A[ind,ind] = 1.0
        return A
    def right(self):
        b = np.zeros([self.Nodes_size,1])#self.Nodes_size = (M + 1)*(N + 1)
        for m in range(self.Units_size):#self.Units_size = M*N
            for k in range(4):
                ind = self.Units_Nodes[m,k]#第m个单元区域内第k个网格点，第k个基函数的编号
                b[ind] += self.Int_F_basic(ind,m)
        for j in range(1,self.nx[1]):
            ind = j
            x = torch.tensor(self.Nodes[ind:ind + 1,:])
            b[ind,0] = bd_y(x).numpy()
            
            ind  = self.nx[0]*(self.nx[1] + 1) + j
            x = torch.tensor(self.Nodes[ind:ind + 1,:])
            b[ind,0] = bd_y(x).numpy()
            
        
        for i in range(self.nx[0] + 1):
            ind = i*(self.nx[1] + 1)
            x = torch.tensor(self.Nodes[ind:ind + 1,:])
            b[ind,0] = bd_y(x).numpy()
            ind = (i + 1)*(self.nx[1] + 1) - 1
            x = torch.tensor(self.Nodes[ind:ind + 1,:])
            b[ind,0] = bd_y(x).numpy()
           
        return b
    def Uh(self,X):
        uh = np.zeros(X.shape[0])
        A = self.matrix()
        b = self.right()
        Nodes_V = np.linalg.solve(A,b)
        for i in range(self.Nodes_size):#self.Nodes_size = (M + 1)*(N + 1)
            # 计算数据集 关于 基函数中心 的相对位置
            uh += Nodes_V[i]*self.basic(X,[0,0],i)
        return uh.reshape(-1,1)
fenet = FENET(bound,nx = [20,20])
n = 64
x_train = np.linspace(bound[0,0],bound[0,1],n + 1)
y_train = np.linspace(bound[1,0],bound[1,1],n + 1)
xx,yy = np.meshgrid(x_train,y_train)
x0 = xx.reshape(-1,1)
x1 = yy.reshape(-1,1)

x_t = torch.from_numpy(np.hstack([x0,x1])).type(dtype).to(device)
fenet_y = fenet.Uh(np.hstack([x0,x1])).flatten()
u_pred = pred_f(netu,x_t).cpu().detach().numpy().flatten()
data_f = pred_f(netu,data_x).cpu().t()
y_pred = pred_u(solvernet,data_f,x_t).cpu().detach().numpy().flatten()
err = (y_pred - fenet_y).reshape(-1,1)
L1 = max(abs(err))
L2 = (err**2).sum()
print('test error:L1:%.2e,L2:%.2e'%(L1,L2))